TRƢỜNG ĐẠI HỌC MỎ ĐỊA CHẤT
BỘ MÔN TOÁN
BÀI GIẢNG
PHƢƠNG PHÁP TÍNH
THÁNG 09/2014
1
Chƣơng 1. SAI SỐ
--------------------------------------------------------------------------------------------------
Trong các bài toán ky thuâ t, giá tri các đa i lưng dùng trong tính toán thưng
không đưc biê t mô t cách chính xác . Chúng ta làm viê c chu yê u với giá tri gâ n đúng cu a
các đa i lưng mà thôi. Khi đó, độ lệch giữa giá trị gần đúng và giá trị đúng gọi là sai số.
1. Số xấp xỉ. Gọi a là số xấp xỉ của số đúng A, nếu a sai khác A không đáng kể và đƣợc
dùng thay cho A trong tính toán. Ký hiệu là a ≈ A.
2. Sai số tuyệt đối. Đại lƣợng ∆a = |a - A| đƣợc gọi là sai số tuyệt đối của của số xấp xỉ a.
Thực tế, không biết số đúng A, nên cũng không thể biết chính xác sai số tuyệt đối. Vì vậy,
ta gọi sai số tuyệt đối cu a số xấp xỉ a là đại lƣợng ∆a, càng bé càng tốt, sao cho |a - A| ≤ ∆a.
Từ bất đẳng thức trên, ta có a - ∆a ≤ A ≤ a - ∆a.
Vậy giá trị của số đúng A đƣợc viết nhƣ sau: A = a ± ∆a.
3. Sai số tƣơng đối.
Đại lƣợng
a
aa
gọi là sai số tƣơng đối của số a.
Sai số tƣơng đối cho biết mức độ tin cậy của số xấp xỉ. Sai số tuyệt đối không phản ánh
đƣợc điều đó. Giả sử đo chiều dài của hai cung đƣờng, đƣợc kết qủa:
S1 = 1500m ± 50cm
S1 = 10m ± 50cm
Hai phép đo có cùng sai sô tuyê t đô i nhƣng phép đo trƣc chính xác hơn phép đo sau.
4. Chữ sô đáng tin. Cho số xấp xỉ a vi sai số ∆a. Giả sử a đƣợc viết dƣi dạng thập phân
1 1 2
1 0 1 2
1 0 1 2
10 10 ... 10 ... 10 ... 10
.... , ...
n n m
n n m m
n n m
a a a a a a a a
hay a a a a a a a
Chữ số ak đƣợc gọi là đáng tin nếu
.
Chữ số ak đƣợc gọi là đáng nghi nếu
10 / 2 10 2
kk
aa
.
Ví dụ: cho a = 21.53674, sai số Δ = 0.004. Có 2≤Các chữ số đáng tin là các
chữ số trƣc chữ số thập phân thứ 2, đó là 2,1,5,3. Các chữ số còn lại là đáng nghi.
Nếu sai số là Δ = 0.006. Thì 2Δ = 0.012 ≤ 10-1. Chữ số đáng tin là chữ số thập phân thứ
nhất. Các chữ số thập phân còn lại là đáng nghi.
5. Cách viết số xấp xỉ.
Cách thứ nhất: Viết số xấp xỉ kèm theo sai số tuyệt đối. Chẳng hạn 12,345 ± 0,005. Cách
này dùng để biểu diễn kết quả tính hoặc phép đo.
2
Cách thứ hai: Viết số xấp xỉ theo quy tắc: Mọi chữ số có nghĩa đều đáng tin. Ví dụ khi viết
a = 1.26 thì sai số đƣợc hiểu là 0.005 (hoặc nhỏ hơn). Cách này thƣờng dùng trong các
bảng số lập sẵn.
6. Sự quy tròn số. Khi tiến hành tính toán, nếu số a có quá nhiều chữ số không tiện cho
tính toán hoặc không ghi hết đƣợc vào máy tính, ta phải bỏ đi vài chữ số cuối để nhận đƣợc
số gần đúng a1. Việc làm đó gọi là sự quy tròn. Biểu thức | a - a1| đƣợc gọi là sai số quy
tròn.
Quy tròn số phải theo quy tắc: Sai số quy tròn không đƣợc vƣợt quá nửa đơn vị của chữ số
giữ lại cuối cùng bên phải. Nhƣ vậy, nếu chữ số bỏ đi đầu tiên ln hơn hoặc bằng 5 thì
thêm 1 vào chữ số giữ lại cuối cùng. Nếu chữ số bỏ đi đầu tiên nhỏ hơn 5 thì giữ nguyên
chữ số giữ lại cuối cùng.
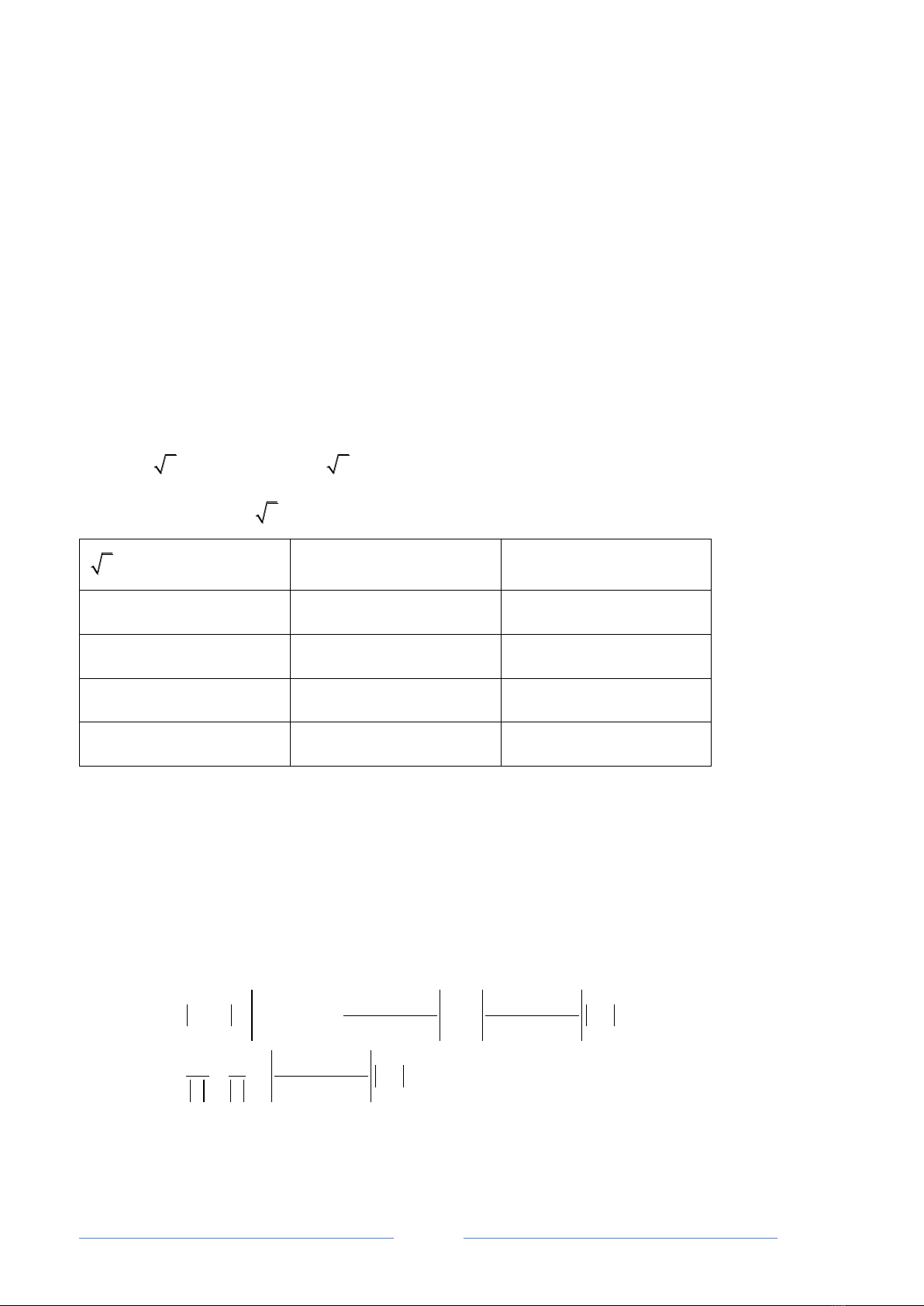
Ảnh hưởng của sai số quy tròn. Xét ví dụ: Nếu khai triển nhị thức Newton, đƣợc công thức
đúng
10
2 1 3363 2378 2
Thay gần đúng giá trị
2
vào hai vế của đẳng thức trên, đƣợc kết quả:
2
vế trái
vế phải
1.4
0.0001048576
33.8
1.41
0.00013422659
10.02
1.41421
0.00014866399
0.00862
1.414213563
0.00014867678
0.0001472
Sự khác biệt ln giữa hai vế chứng tỏ sai số quy tròn gây ra những hậu quả rất đáng ngại.
7. Sai số tính toán.
Khi tính toán biểu thức số học f(x1,...,xn), từ sai số của đối số xi, ta nhận đƣợc sai số của kết
quả tính biểu thức. Sai số này có thể sẽ rất ln.
a) Công thức tổng quát. Giả sử phải tính biểu thức u = f(x1,...,xn), vi sai số của mỗi xi là
Δi. Gọi Xi và Ui là giá trị đúng của của các số xấp xỉ xi, ui tƣơng ứng. Theo công thức số
gia hữu hạn, có
11
11
1
1
,..., ,...,
,...,
1
nn
nn
i i i
ii
ii
nn
i
ii
f x x f x x
u U u X x x
xx
f x x
u
ux
u u x




b) Sai số của tổng. Xét tổng u = x1 + x2 +...+ xn. Theo công thức tổng quát, hoặc tính trực
tiếp, ta đƣợc
3
1
1
...
...
n
n
u x x
xx
uu
Chú ý về sai số của hiệu. Nếu x1 - x2 nhỏ thì sai số Δu có thể rất ln. Vì vậy ngƣời ta
thƣờng tránh thực hiện phép trừ hai số gần nhau bằng cách biến đổi biểu thức nếu có thể.
Ví dụ: Tính hiệu u =
2,01 2
,
Nếu lấy
2,01 1,42, 2 1,42
thì u = 0,01. Sai số trong trƣờng hợp này là
Δ = (0,005 + 0,005) / (1,42 - 1,41) = 1.
Nếu viết u dƣi dạng
2.01 2 2.01 2 2.01 2 0.01 0,00353
1,42 1,41 2,83
2.01 2
u
Sai số Δ = (0,005 + 0,005) / (1,42 +1,41) = 0,005
Rõ ràng kết quả tốt hơn và sai số trong trƣờng hợp này nhỏ hơn nhiều cách tính trực tiếp.
c) Sai số của tích và thương. Theo công thức tổng quát: nếu u = x1x2 hoặc u = x1/x2, đều có
Δu = |u|(Δx1 + Δx2)
Δu = (Δx1 + Δx2)
8. Sai số phƣơng pháp.
Nói chung các phƣơng pháp giải bài toán là các phƣơng pháp gần đúng. Sai số xuất hiện do
cách giải gọi là sai số phƣơng pháp. Mỗi phƣơng pháp thƣờng có một sai số nhất định.
Loại sai số này sẽ đƣợc nghiên cứu trong từng phƣơng pháp cụ thể.
9. Bổ sung: Kỹ năng sử dụng máy tính Casio - f 500.
a) Ô nhớ thanh tổng Ans: Để gán giá trị cho Ans, ta bấm giá trị cần gán rồi bấm dấu =.
Từ lúc này, giá trị ô nhớ thanh tổng đưc duy trì cho đến khi gặp lệnh gán khác.
b) Thực hiện phép tính lặp: Ví dụ cần tính xn+1 = xn2 - 2xn + 4, với x1 = 1. Thực hiện theo
thứ tự sau: Gán 1 cho ans / bấm ans ans - 2ans + 4 / bấn dấu = liên tiếp n+1 lần.
c) Sử dụng ô nhớ khác: Để gán giá trị cho ô nhớ bất kỳ (có 9 ô nhớ), ta bấm giá trị cần
gán, rồi bấm lần lưt Shift / Sto (phím RCL) / bấm chữ cái là tên ô nhớ. Có 9 chữ cái là a
(phím (-)), b (phím ,,,), c (phím hyp) v.v... .
Muô n sư du ng gia tri cu a ô nhơ na o đo , bâ m Alpha / bâ m phim chư tương ư ng.