
Ch ng Iươ
Bài 1
S c b n v t li uứ ề ậ ệ
NH NG KHÁI NI M C B N V S C B N V T LI UỮ Ệ Ơ Ả Ề Ứ Ề Ậ Ệ
Ch ng 1:ươ CÁC KHÁI NI MỆ
Phân tinh hoc:
I. Nhi m v và đi t ng nghiên c u ệ ụ ố ượ ứ
1 Nhi m v ệ ụ
Khi thi t k các b ph n c ng trình ho c các chi tti t máy ta ph i b o đm ế ế ộ ậ ộ ặ ế ả ả ả
Chi ti t không b phá h ng t c là đ b n ế ị ỏ ứ ủ ề
Chi ti t không b bi n d ng quá l n t c là đ c ng ế ị ế ạ ớ ứ ủ ứ
Luôn gi đc hình dáng cân b ng ban đu t c là đm b o đi u ki n n đnh ữ ượ ằ ầ ứ ả ả ề ệ ổ ị
Đ đm b o đc đi u ki n đó trên c s c a c lý thuy t môn s c b n v t li u có ể ả ả ượ ề ệ ơ ở ủ ơ ế ứ ề ậ ệ
nhi m v đa ra ph ng pháp tính toán v đ b n , đ c ng , đ n đnh c a các b ệ ụ ư ươ ề ộ ề ộ ứ ộ ổ ị ủ ộ
ph n công trình ho c các chi ti t máy ậ ặ ế
1.2 Đi t ng nghiên c u ố ượ ứ
Đi t ng nghiên c u c a môn s c b n là các v t r n bi n d ng mà ch y u là các ố ượ ứ ủ ứ ề ậ ắ ế ạ ủ ế
thanh
Thanh là nh ng v t th có kích th c theo hai ph ng nh h n so v i ph ng th 3 ữ ậ ể ướ ươ ỏ ơ ớ ươ ứ
F di n tích m t c t ngang c a thanh là giao c a thanh v i m t ph ng vuông góc v i tr c ệ ặ ắ ủ ủ ớ ặ ẳ ớ ụ
thanh
M t c t ngang c a thanh và tr c tr c thanh là y u t đc tr ng cho mô hình c a thanh ặ ắ ủ ụ ụ ế ố ặ ư ủ
1.2. Các khái ni mệ
1
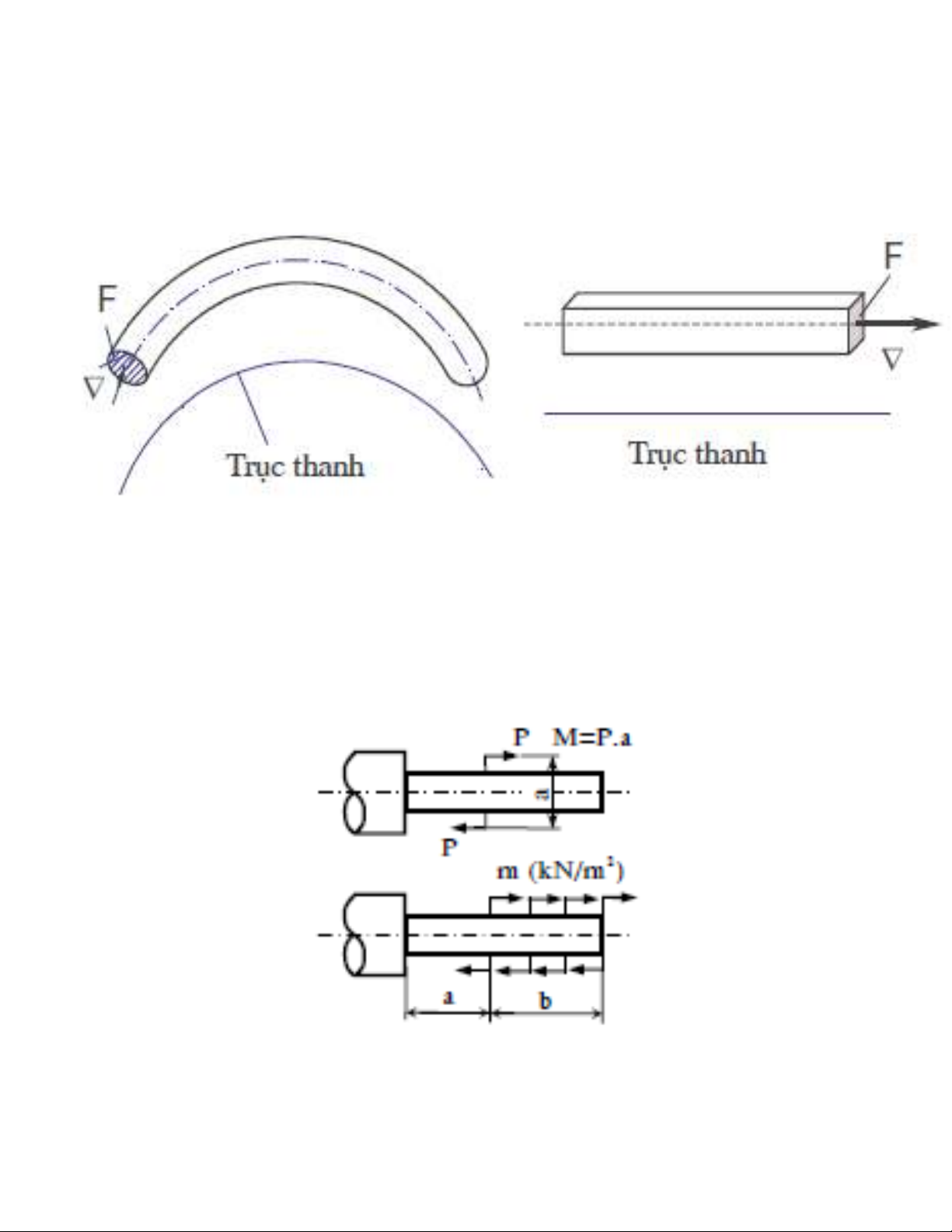
Thanh là m t v t th d c t o ra do m t hình ph ng F có ti t di n là hình tròn hay ch ộ ậ ể ượ ạ ộ ẳ ế ệ ữ
nh t di chuy n trong không gian sao cho tr ng tâm C c a nó luôn trên m t đo n đng ậ ể ọ ủ ở ộ ạ ườ
cong trong không gian, còn hình ph ng luôn vuông góc v i đng cong ẳ ớ ườ .
2. T i tr ng ả ọ
2.1. Đnh nghĩaị
T p h p t t c các tác d ng bên ngoài , tác d ng vào v t kh o sát.ậ ợ ấ ả ụ ụ ậ ả
2.2. Phân lo iạ
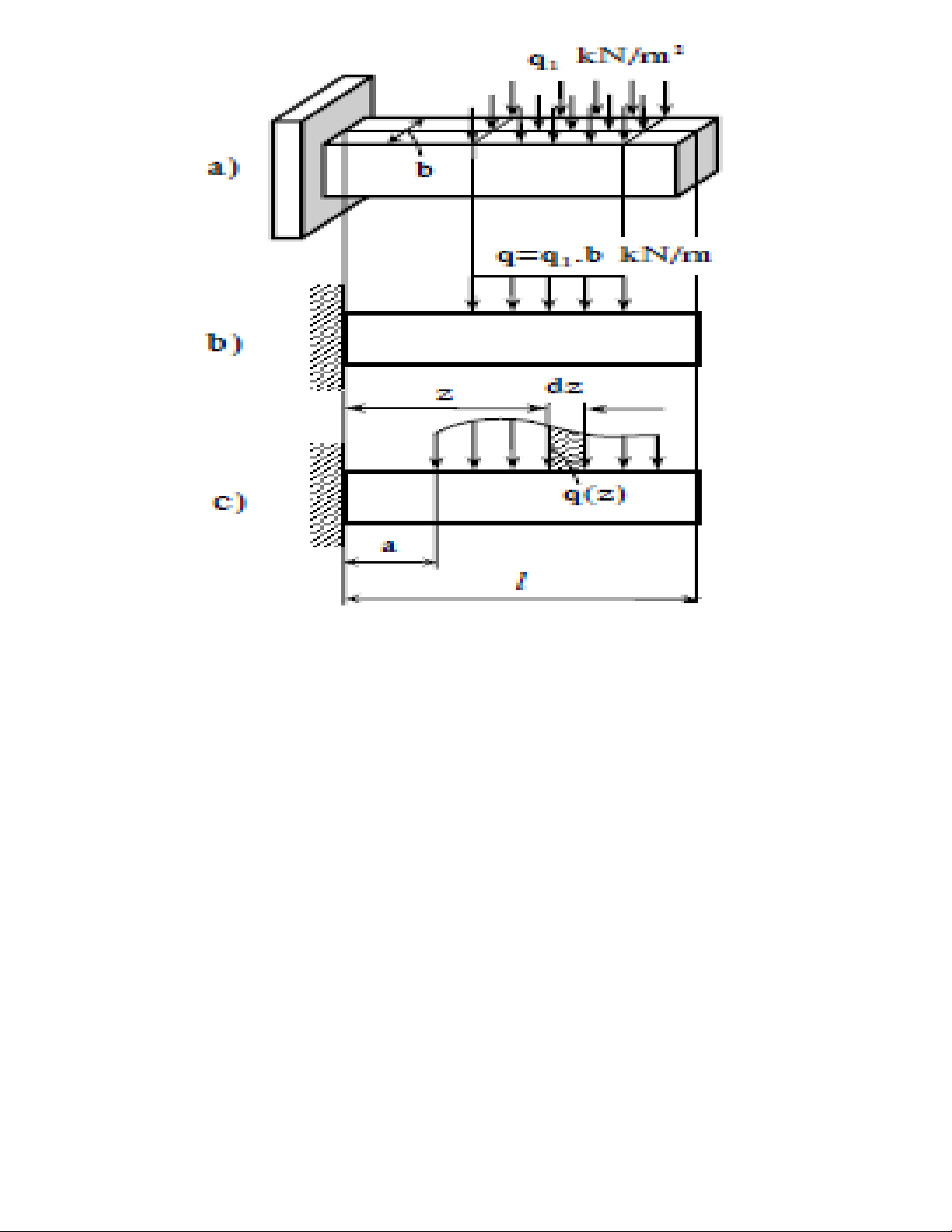
T i tr ng g m l c t p trung, l c phân b , moment t p trung và phân bả ọ ồ ự ậ ự ố ậ ố
2
II Ngo i l c N i l c và ng su t ạ ự ộ ự ứ ấ
1 Ngo i l c ạ ự
1.1Đnh nghĩaị
Ngo i l c là nh ng l c tác đng t môi tr ng bên ngoài hay t v t khác lên v t đang xét ạ ự ữ ự ộ ừ ườ ừ ậ ậ
1.2 Phân lo i ạ
Ngo i l c g m ạ ự ồ
T i tr ng đã bi t tr c ả ọ ế ướ
Ph n l c phát sinh t i các liên k t ả ự ạ ế
2 N i l cộ ự
Đnh nghĩa ị
D i tác d ng c a ngo i l c v t th b bi n d ng , gi a các ph n t c a v t xu t hi n ướ ụ ủ ạ ự ậ ể ị ế ạ ữ ầ ử ủ ậ ấ ệ
thêm ph n l c tác d ng t ng h đ ch ng l i tác d ng c a ngo i l c. Ph n l c đó g i làầ ự ụ ươ ỗ ể ố ạ ụ ủ ạ ự ầ ự ọ
n i l c ộ ự
3
2 Ph ng pháp m t c t ươ ặ ắ
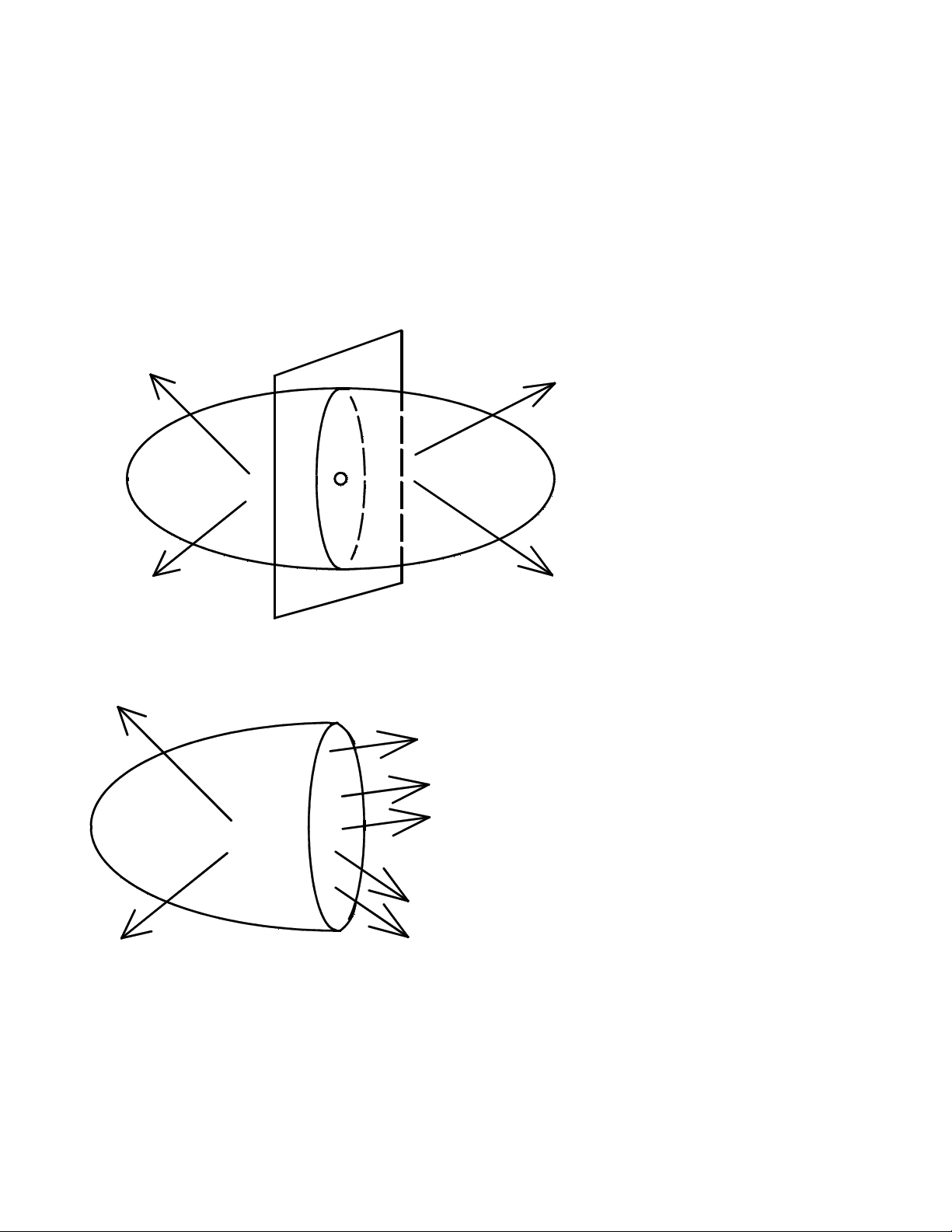
Khi v t th ch a b phá ho i thì n i l c cân b ng v i ngo i l c . Vì th đ kh o sát n i ậ ể ư ị ạ ộ ự ằ ớ ạ ự ế ể ả ộ
l c ta dùng ph ng pháp m t c t nh sau ự ươ ặ ắ ư
V t ch u l c tr ng thái cân b ng ậ ị ự ở ạ ằ
Đ tìm n i l c t i C ta t ng t ng dùng m t ph ng ể ộ ự ạ ưở ượ ặ ẳ
π
qua C c t v t ra làm hai ph n A,Bắ ậ ầ
. Xét ph n A cân b ng d i tác d ng c a các ngo i l c ầ ằ ướ ụ ủ ạ ự
1 2
,P P
và l c tác d ng ự ụ
t ng h t các ph n B t c là các n i l c ươ ỗ ừ ầ ứ ộ ự
N i l c phân b liên t c trên di n tích F c a m t c t ộ ự ố ụ ệ ủ ặ ắ
CB
A
P3
Pn
P1
P2
A
P1
P2 F
3. ng su tỨ ấ
C ng đ c a n i l c t i m t đi m nào đó trên m t c t đc g i là ng su tườ ộ ủ ộ ự ạ ộ ể ặ ắ ượ ọ ứ ấ
4
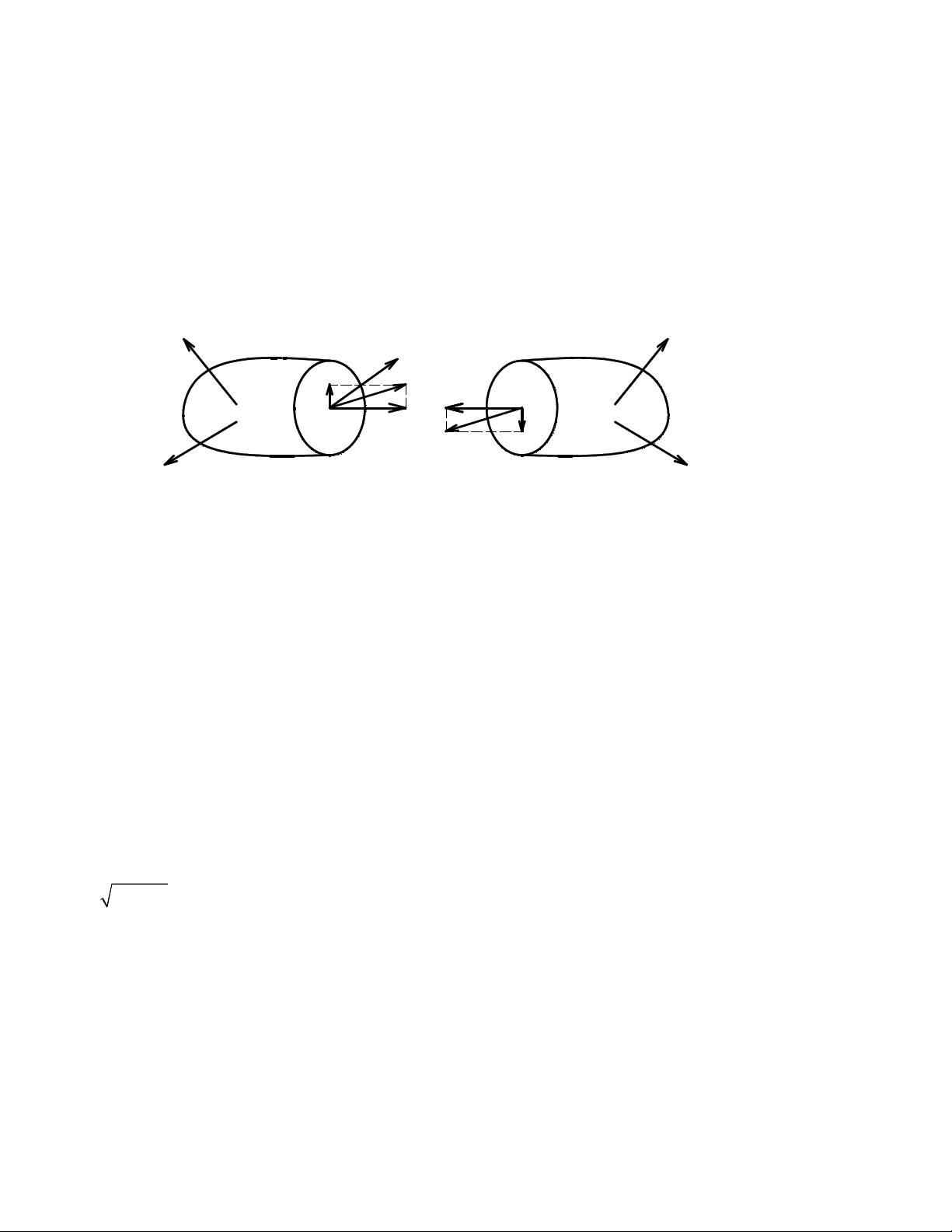
Trong tính toán ta th ng phân ng su t toàn ph n ườ ứ ấ ầ
P
ra làm hai thành ph n ầ
P
C
P
1
P
2
P
P3
Pn
A B
Thành ph n vuông góc v i m t c t g i là ng su t pháp , ầ ớ ặ ắ ọ ứ ấ
σ
: ng su t phápứ ấ
Thành ph n n m trong m t c t g i là ng su t ti p, ầ ằ ặ ắ ọ ứ ấ ế
τ
: ng su t ti p ứ ấ ế
2 2
P
σ τ
= +
4. Các thành phàn n i l c trên m t c t ngangộ ự ặ ắ
L c d c Nz;ự ọ
L c c t Qx, Qy; ự ắ
Mômen u n Mx, My; ố
Mômen xo n Mz.ắ
5


















![Bài giảng Quản lý vận hành và bảo trì công trình xây dựng [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251006/agonars97/135x160/30881759736164.jpg)







