Ngô Văn Cường- Industrial University Of HCM City 1/92
02/08/2015
Ngô Văn Cường
Đại học công nghiệp TPHCM
(Serious learning is the key to success.)
Strength Of Materials
SỨC BỀN
VẬT LIỆU
Ngô Văn Cường- Industrial University Of HCM City 2/92
02/08/2015
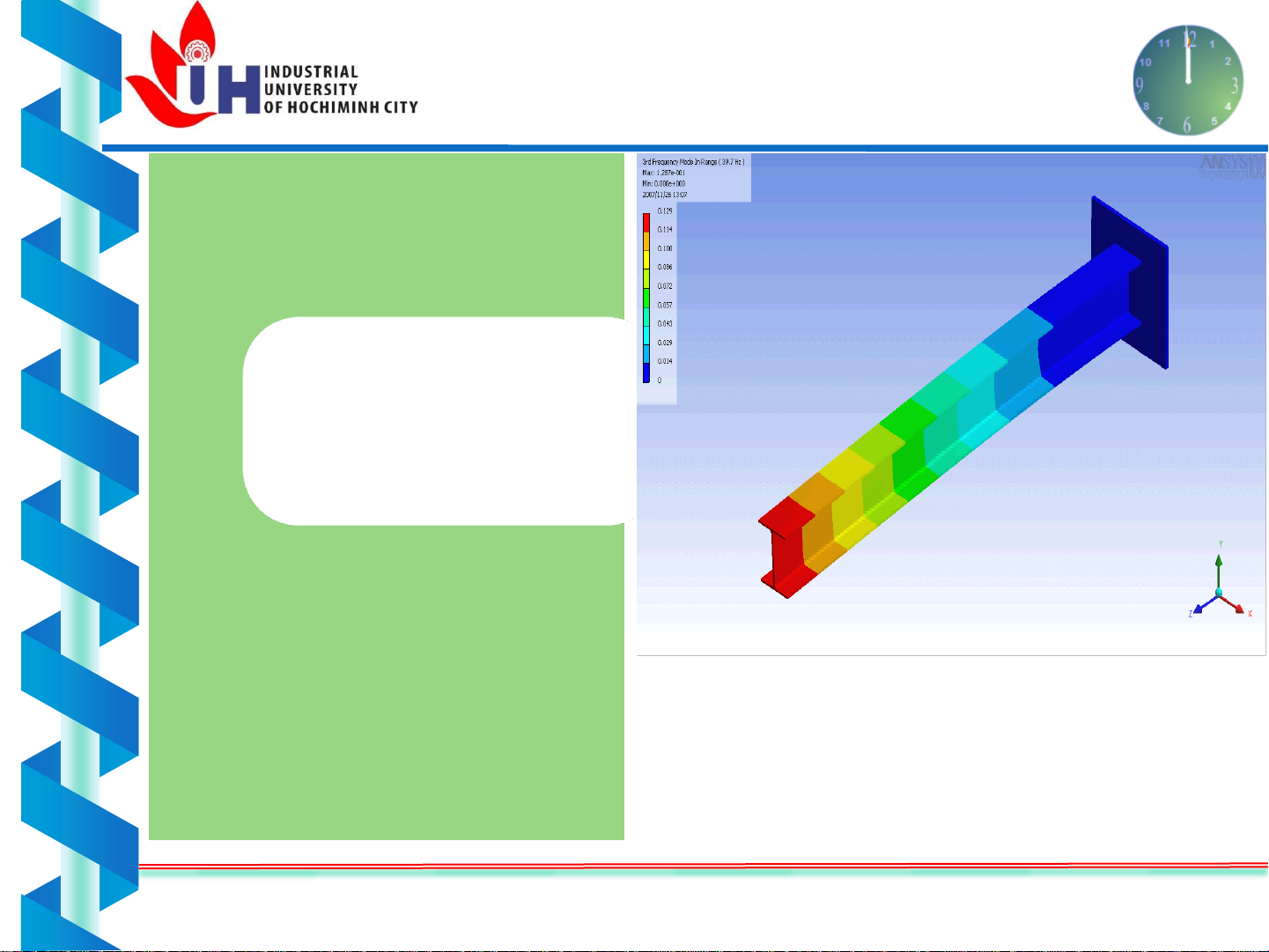
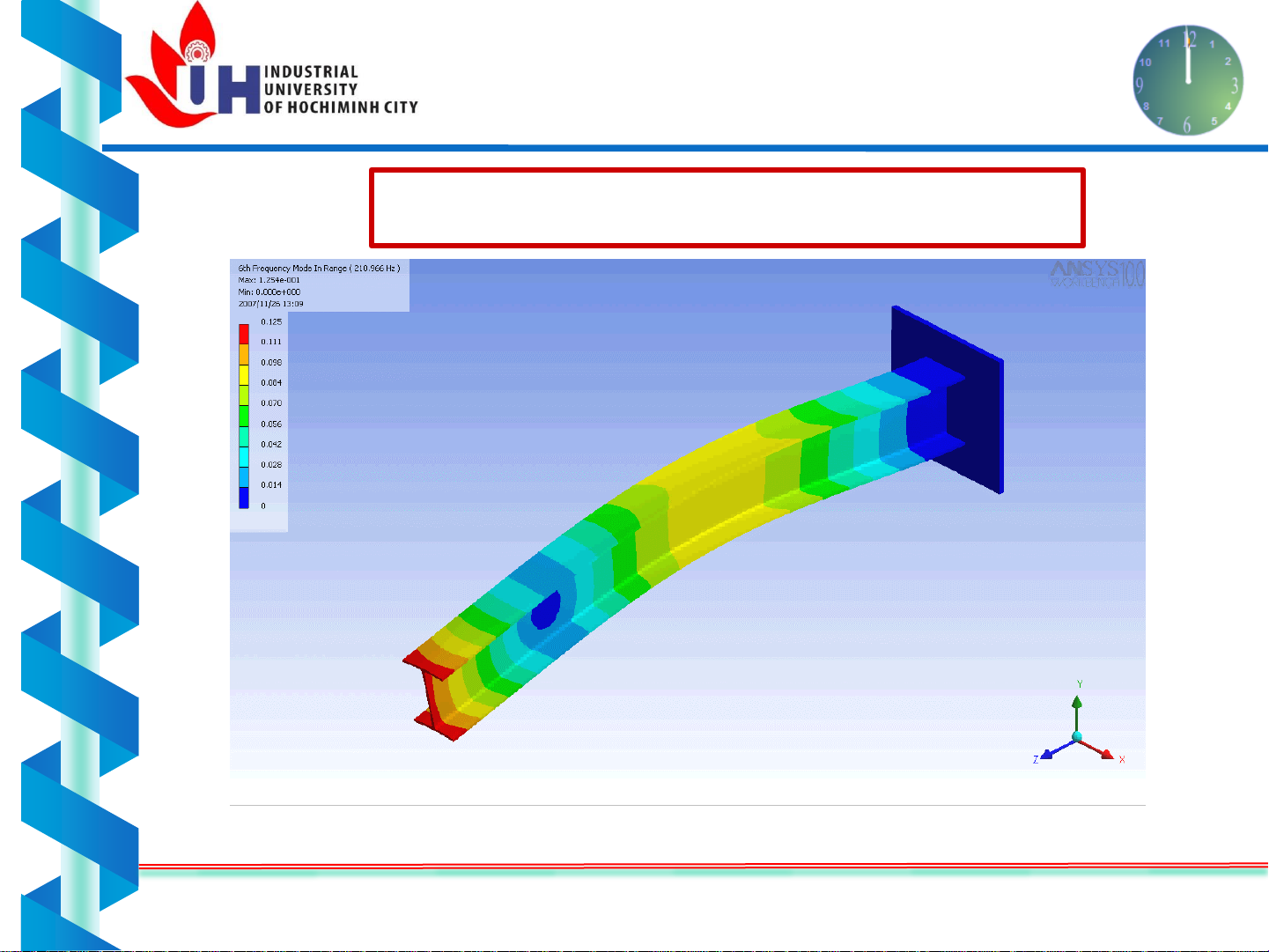
Chuyển vị của dầm chịu uốn
UỐN PHẲNG THANH THẲNG
Ngô Văn Cường- Industrial University Of HCM City 3/92
02/08/2015
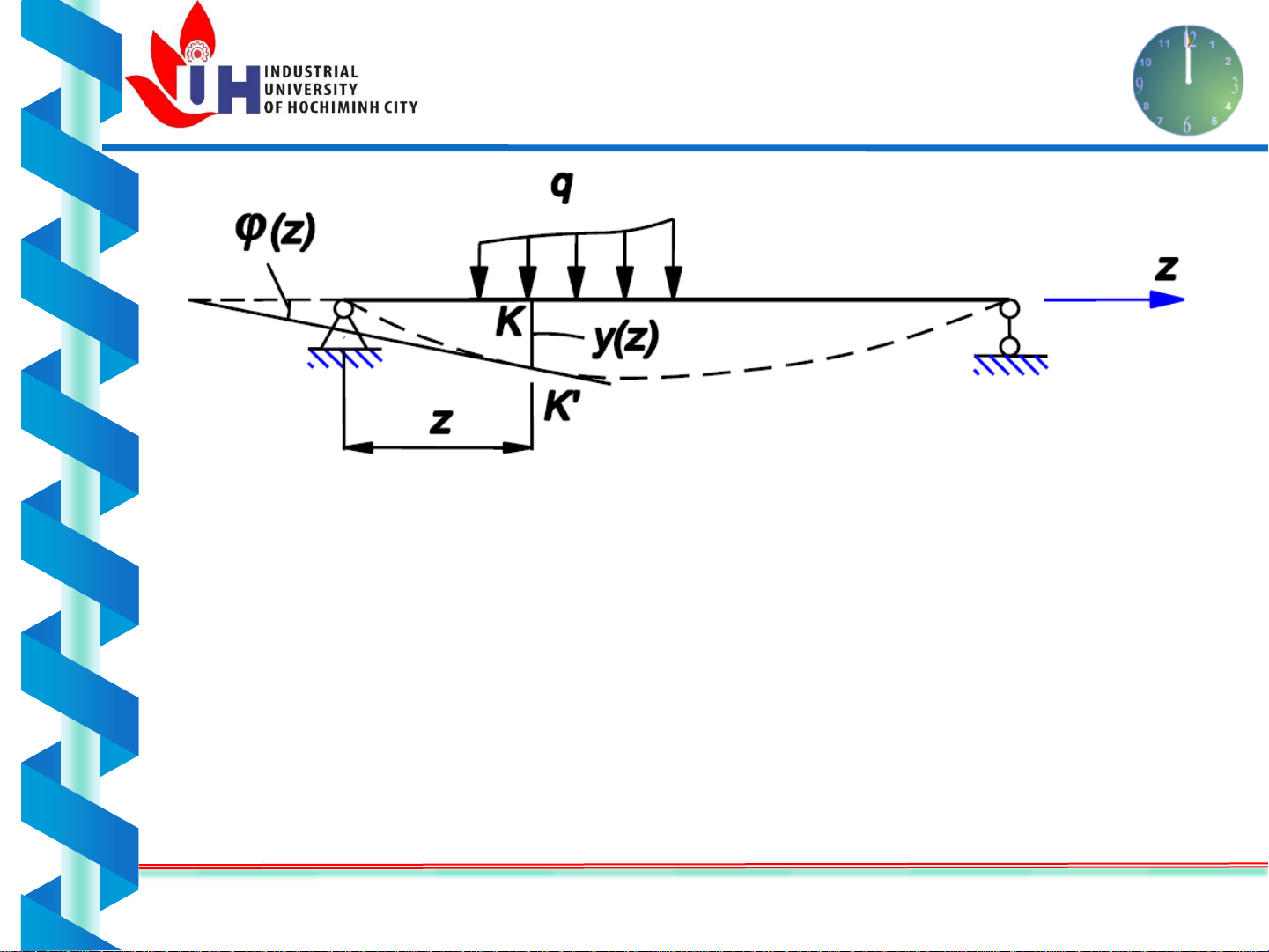
Chuyển vị của dầm chịu uốn
Khi dầm chịu uốn phẳng ⇒trục của dầm bị
uốn cong gọi là đường đàn hồi
Chuyển vị đứng của MCN tại K gọi là độ
võng y(z) của dầm.
Ngô Văn Cường- Industrial University Of HCM City 4/92
02/08/2015
Chuyển vị của dầm chịu uốn
Góc lập bởi tiếp tuyến với đường đàn hồi tại
điểm K’ và trục của dầm trước khi biến dạng
gọi là góc xoay ϕ(z).
1. Phương trình vi phân gần đúng của đường
đàn hồi.
Từ mối quan hệ giữa moment uốn Mxvà ứng
suất pháp
z
Ngô Văn Cường- Industrial University Of HCM City 5/92
02/08/2015
Chuyển vị của dầm chịu uốn
1x
x
M
EI
Ta có bán kính cong của đường đàn hồi được
xác định
Mặt khác ta có
''
3
'2 2
1
1
y
y
