Tr riêng, véct riêng c a ma tr nị ơ ủ ậ
--------------------------------------------------------------------------------------------------------------------------
-
v
Av
u
Au
Ví d .ụ
3 2
1 0
A
−
� �
=� �
� �
1
1
u
−
� �
=� �
� �
2
1
v
��
=��
��
S đ c g i là ố ượ ọ tr riêngị c a A, n u t n t i véct x ủ ế ồ ạ ơ khác
không, sao cho .
Ax x
λ
=
λ
Khi đó, véct x đ c g i là ơ ượ ọ véct riêngơ c a ma tr n vuông ủ ậ
A t ng ng v i tr riêng . ươ ứ ớ ị
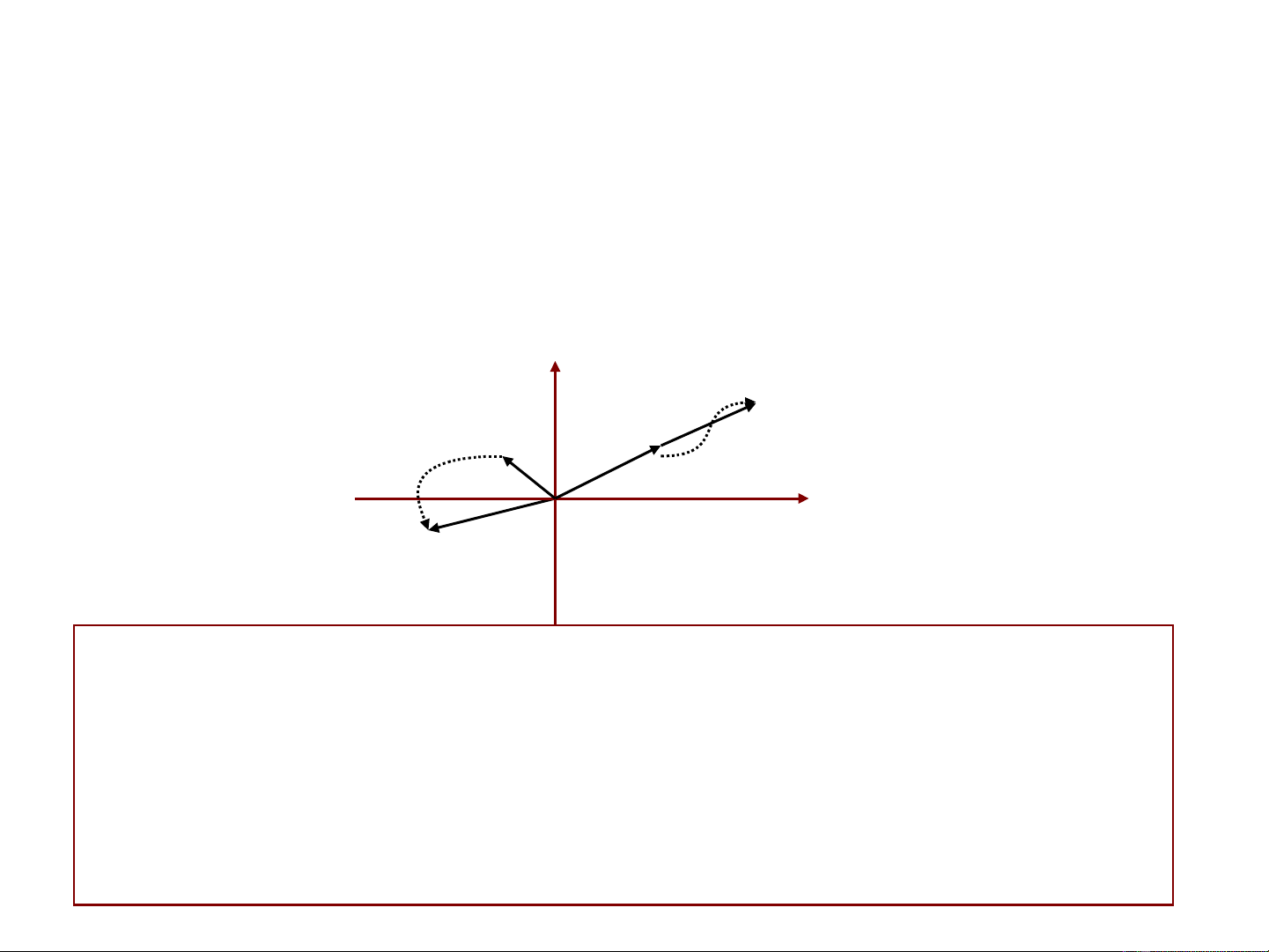
λ
Tính và . Hãy cho bi t nh n xét. ế ậ
Au
Av
Tr riêng, véct riêng c a ma tr n ị ơ ủ ậ
--------------------------------------------------------------------------------------------------------------------------
-
Gi iả 1 6 6 24
5 2 5 20
−
� �� � � �
= =
� �� � � �
−
� �� � � �
Au
Ví dụ
1 6
5 2
A� �
=� �
� �
6
5
u� �
=� �
−
� �
3
2
v� �
=� �
−
� �
Véct nào là véct riêng c a ơ ơ ủ A?
Ta có 4.Au u= − là véct riêng ơ
u
1 6 3 9
5 2 2 11
−
� �� � � �
= =
� �� � � �
−
� �� � � �
Av
Không t n t i s đ ồ ạ ố ể
λ
Av v
λ
=không là véct riêng ơ
v
6
4 4.
5
u
� �
= − = −
� �
−
� �
Tr riêng, véct riêng c a ma tr n ị ơ ủ ậ
--------------------------------------------------------------------------------------------------------------------------
-
Gi i.ả Xét h ph ng trình ệ ươ 1
Ax x
λ
=
Ví d .ụ
3 4
6 5
A� �
=� �
� � 1 2
1; 3
λ λ
= − =
S nào là tr riêng c a A?ố ị ủ
1 1
2 2
3 4 1
6 5
x x
x x
� � � �
� � = −�� � � �
� �
� �
� � � �
1 2
1 2
4 4 0
6 6 0
x x
x x
+ =
+ =
H này có vô s nghi m, nên t n t i m t nghi m ệ ố ệ ồ ạ ộ ệ khác không,
ví d ụ1
1
x� �
=� �
−
� � khi đó 1.
λ
=Ax x
V y là tr riêng. ậ ị
1
λ
Ki m tra t ng t th y không là tr riêng. ể ươ ự ấ ị
2
λ
Tr riêng, véct riêng c a ma tr n ị ơ ủ ậ
--------------------------------------------------------------------------------------------------------------------------
-
H thu n nh t có nghi m ệ ầ ấ ệ khác không
V y là tr riêng khi và ch khi là nghi m c a ph ng ậ ị ỉ ệ ủ ươ
trình đ c tr ng. ặ ư
λλ
Gi s là tr riêng c a ma tr n A ả ử ị ủ ậ
0
λ
0 0 0 0
0:x Ax x
λ
∃ =� �
0 0 0 0Ax x
λ
− =�0 0
( ) 0A I x
λ
− =�
0
det( ) 0A I
λ
− =�
Đa th c g i là ứ ọ đa th c đ c tr ngứ ặ ư c a A.ủ
( ) det( )
A
P A I
λ λ
= −
đ c g i là ượ ọ ph ng trình đ c tr ngươ ặ ư c a ủ
ma tr n vuông A.ậ
det( ) 0A I
λ
− =
Tr riêng, véct riêng c a ma tr n ị ơ ủ ậ
--------------------------------------------------------------------------------------------------------------------------
-
B c 1ướ . L p ph ng trình đ c tr ng ậ ươ ặ ư det( ) 0.
λ
− =A I
(Tính đ nh th c v trái, ta có ph ng trình b c n theo ) ị ứ ở ế ươ ậ
λ
Tìm tr riêng, véct riêng c a ma tr n vuông A c p n.ị ơ ủ ậ ấ
B c 2ướ . Gi i ph ng trình đ c tr ng. T t c các nghi m ả ươ ặ ư ấ ả ệ
c a ph ng trình đ c tr ng là tr riêng c a A và ng c l i. ủ ươ ặ ư ị ủ ượ ạ
B c 3ướ . Tìm VTR c a A t ng ng TR (ch ng h n) ủ ươ ứ ẳ ạ
1
λ
1
( ) 0.
λ
− =A I X
b ng cách gi i h ph ng trình ằ ả ệ ươ
T t c các nghi m khác không c a h là các VTR c a A ng ấ ả ệ ủ ệ ủ ứ
v i tr riêng ớ ị
1
.
λ