07:35
1
TRƯỜNG ĐẠI HỌC THỦ DẦU MỘT
KHOA ĐIỆN - ĐIỆN TỬ
BÀI GIẢNG:
TOÁN KỸ THUẬT
GV: Nguyễn Cao Trí
Bình Dương 2/2016
1 2
1. Tên học phần: TOÁN KỸ THUẬT
2. Số tín chỉ: 3 (2LT+1 TH)
3. Phân bổ thời gian: 60 tiết
- Lý thuyết: 30 tiết;
- Bài tập: 30 tiết.
4. Tiêu chuẩn đánh giá sinh viên:
- Điểm KT giữa học phần: 30%;
- Điểm thi kết thúc học phần: 70%.
3
5. Tài liệu học tập:
5.1. Tài liệu bắt buộc:
Lê Bá Long, “Toán kỹ thuật”
5.2. Tài liệu tham khảo:
[1]. Nguyễn Kim Đính, “Hàm phức và ứng
dụng”, Trường Đại Học Kỹ Thuật Tp Hồ Chí
Minh, 1998.
[2]. Nguyễn Kim Đính, “Phép biến đổi Laplace”,
Trường Đại Học Kỹ Thuật Tp Hồ Chí Minh,
1998.
4
NỘI DUNG
CHƯƠNG 1: HÀM BIẾN PHỨC
CHƯƠNG 2: THẶNG DƯ VÀ ỨNG DỤNG
CHƯƠNG 3: TOÁN TỬ LAPLACE
CHƯƠNG 4: ỨNG DỤNG LAPLACE VÀO
GIẢI TÍCH MẠCH ĐIỆN
CHƯƠNG 5: FOURIER
07:35
2
5
CHƯƠNG 1: HÀM BIẾN PHỨC
1.1. Số phức
1.2. Hàm biến phức
1.3. Giới hạn và liên tục
1.4. Đạo hàm
1.5 Điều kiện Cauchy- Riémann
1.6 Các tính chất của hàm phức
1.7 Các hàm sơ cấp
1.1. Số phức
♦ Số phức có dạng: z = x + iy
i: số ảo đơn vị; i
2
= -1
x = Re{z): phần thực của z
y = Im{z): phần ảo của z.
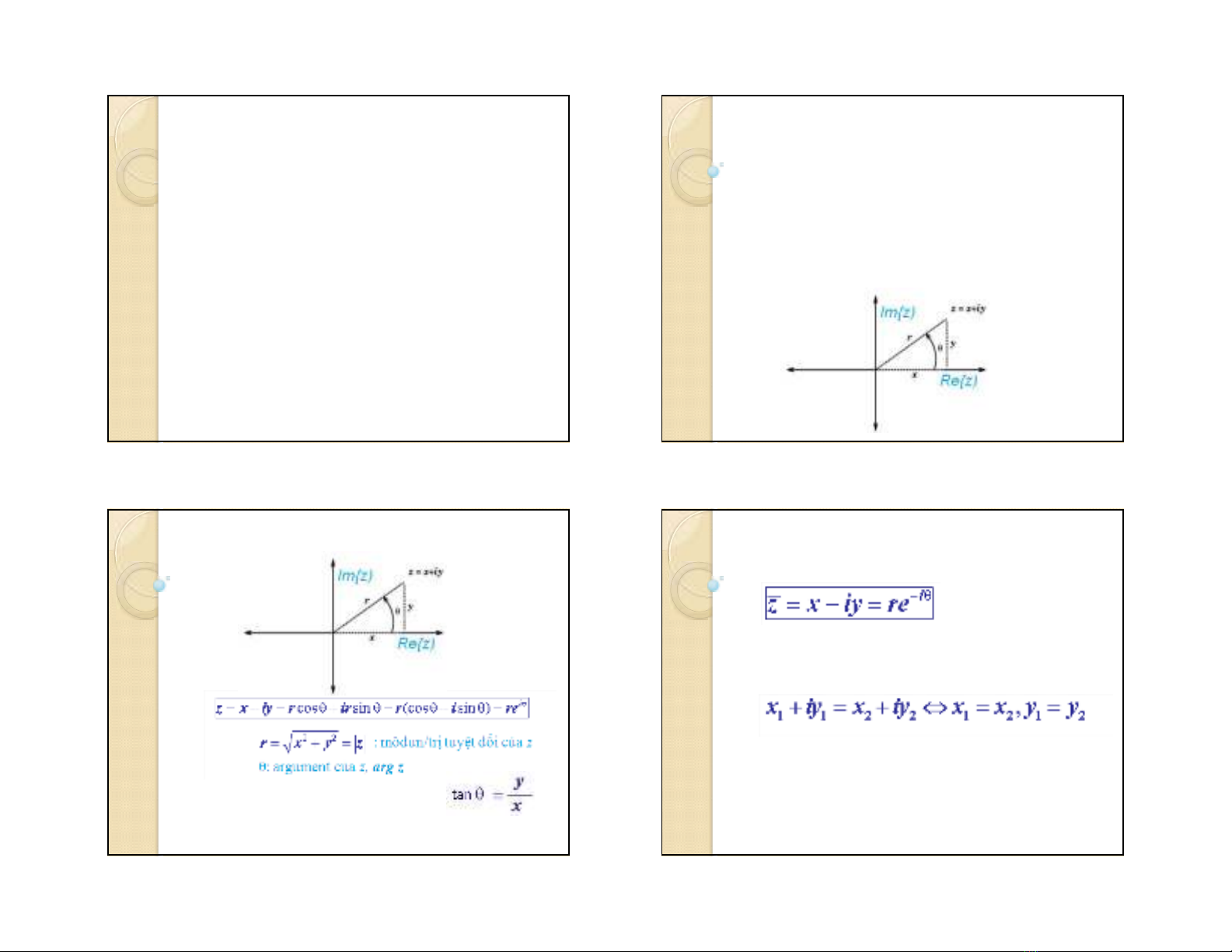
♦ Biểu diễn số phức trong mặt phẳng phức:
6
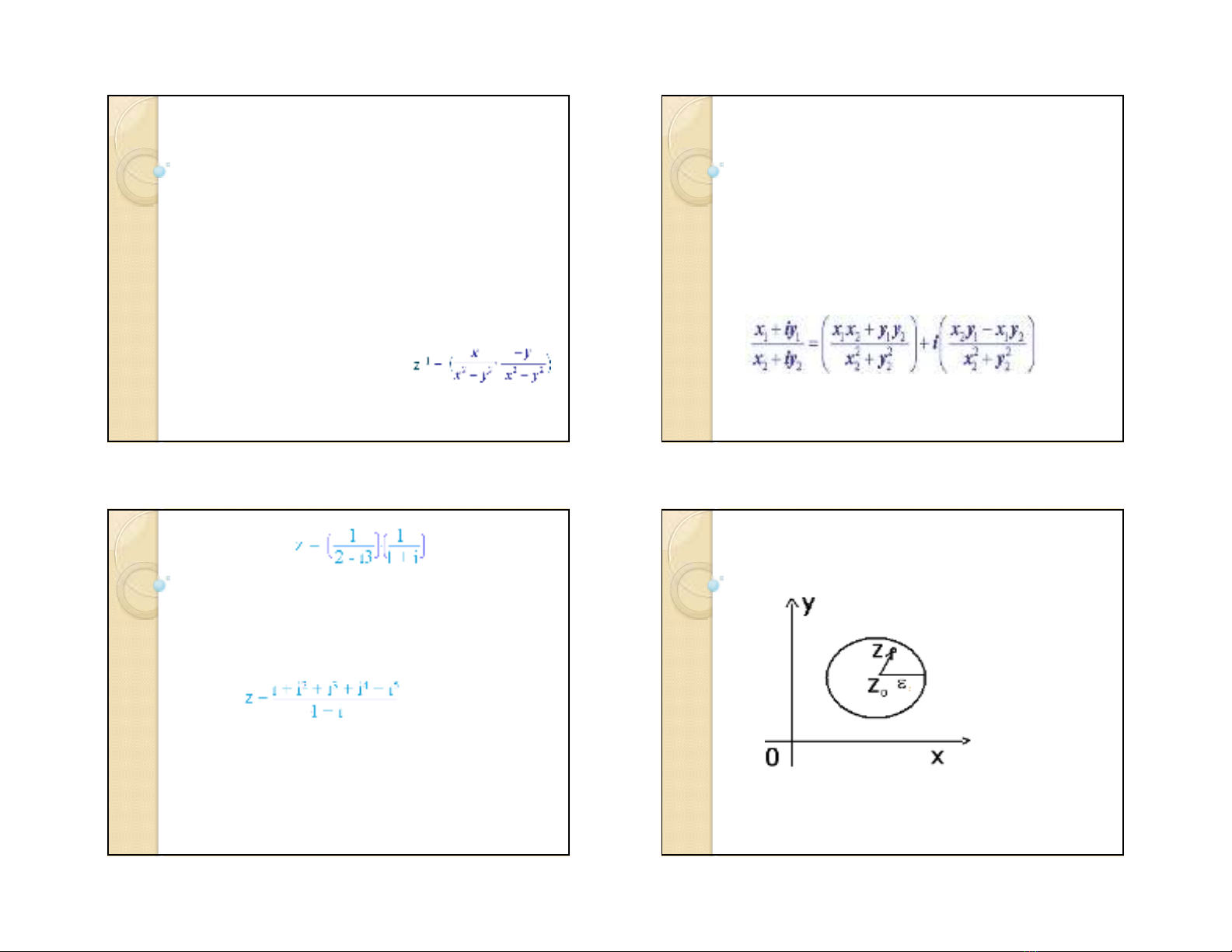
♦ Biểu diễn số phức dưới dạng tọa độ cực:
Giá trị này được tính từ công thức:
7
♦Số phức liên hợp của z = x + iy là số:
♦ Hai số phức z
1
= x
1
+ iy
1
và z
2
= x
2
+ iy
2
bằng
nhau khi:
8
07:35
3
♦ Số phức cũng có các tính chất tương tự như trên số
thực như:
- Giao hoán
- Kết hợp
- Phân bố
- Phần tử đơn vị:
0(0,0): Phần tử đơn vị đối với toán cộng;
1(1,0): Phần tử đơn vị đối với toán nhân.
- Số nghịch đảo
Số nghịch đảo cộng: z = (x,y) và -z = (-x,-y)
Số nghịch đảo nhân: z = (x,y)
và
9
♦ Phép cộng, trừ:
z
1
± z
2
= (x
1
± x
2
) + i(y
1
± y
2
)
♦ Phép nhân:
(x
1
+ iy
1
).(x
2
+ iy
2
) = (x
1
x
2
- y
1
y
2
) + i(x
1
y
2
+ x
2
y
1
)
♦ Phép chia:
10
♦ Ví dụ 1: Tính
♦ Ví dụ 2: Tính x và y nếu: (x + y +2) + (x
2
+ y)i= 0
Giải: Viết 0(0,0) và theo định nghĩa 2 số phức bằng
nhau, ta có: x + y +2 = 0 và x
2
+ y = 0.
Suy ra 2 nghiệm: x=2, y= -4 hoặc x= -1,y= -1.
♦ Ví dụ 3:
♦ Ví dụ:……..
Bài tập: Ví dụ1.4,1.5,……1.13 quyển 1 (Hàm
phức và ứng dụng”, Trường Đại Học Quôc gia Tp
Hồ Chí Minh)
11
1.2. Hàm biến phức
12
07:35
4
MỘT SỐ KHÁI NIỆM
♦Cận (gần nhau): cận ε của điểm z
0
là tập điểm znằm trong
đường tròn tâm z
0
có bán kính ε,
♦Điểm trong/điểm ngoài: điểm z
0
của một tập điểm S được
gọi là nằm bên trong S nếu có một cận của z
0
hoàn toàn nằm
trong S và được gọi là điểm ngoài của S nếu có một cận của z
0
không chứa điểm nào của S.
♦Điểm biên: điểm z
0
được gọi là điểm biên của S nếu z
0
không phải điểm trong cũng không phải điểm ngoài. Viis dụ |z|
= 1 là biên của tập sau: S1: |z| = 1 và S2 : |z| ≤ 1.
♦Tập hở: S được gọi là một tập điểm hở nếu nó không chứa
điểm biên nào, tất cả các điểm của S đều là các điểm trong.
13
♦Vùng: một tập điểm chứa tất cả các điểm của một
tập mở và không/vài/tất cả các điểm biên của nó được
gọi là một vùng, kí hiệu R.
♦Vùng kín ( ): một vùng được gọi là kín nếu nó chứa
tất cả các điểm biên của nó.
♦Vùng có biên: một vùng được gọi là có biên nếu tồn
tại một hằng số M > 0 sao cho tất cả các điểm zcủa
vùng thỏa mãn |z| ≤ M, nghĩa là chúng nằm trong
đường tròn.
♦Vùng kết hợp: một vùng vừa có biên, vừa kín thì
được gọi là kết hợp. Ví dụ, vùng |z| ≤ 1 là vùng kết
hợp vì nó vừa kín và vừa có biên. Vùng |z| < 1 là vùng
mở và có biên
R
14
♦Vùng liên thông: giả sử ta có n điểm z
1
,z
2
, …, z
n
trong
mặt phẳng. Mặt phẳng đó có một đường gấp khúc gồm (n-1)
đoạn theo trình tự , , …, . Một vùng được gọi là
liên thông nếu hai điểm bất kì trong các điểm của nó có thể
được nối bằng đường gấp khúc có trong vùng đó
1 2
z z
2 3
z z
1n n
z z
15
♦Miền: một vùng hở và liên thông được gọi là một miền, kí
hiệu D. Ví dụ, là một miền
không có biên
0 0
{ : arg }
i
S z re z
16
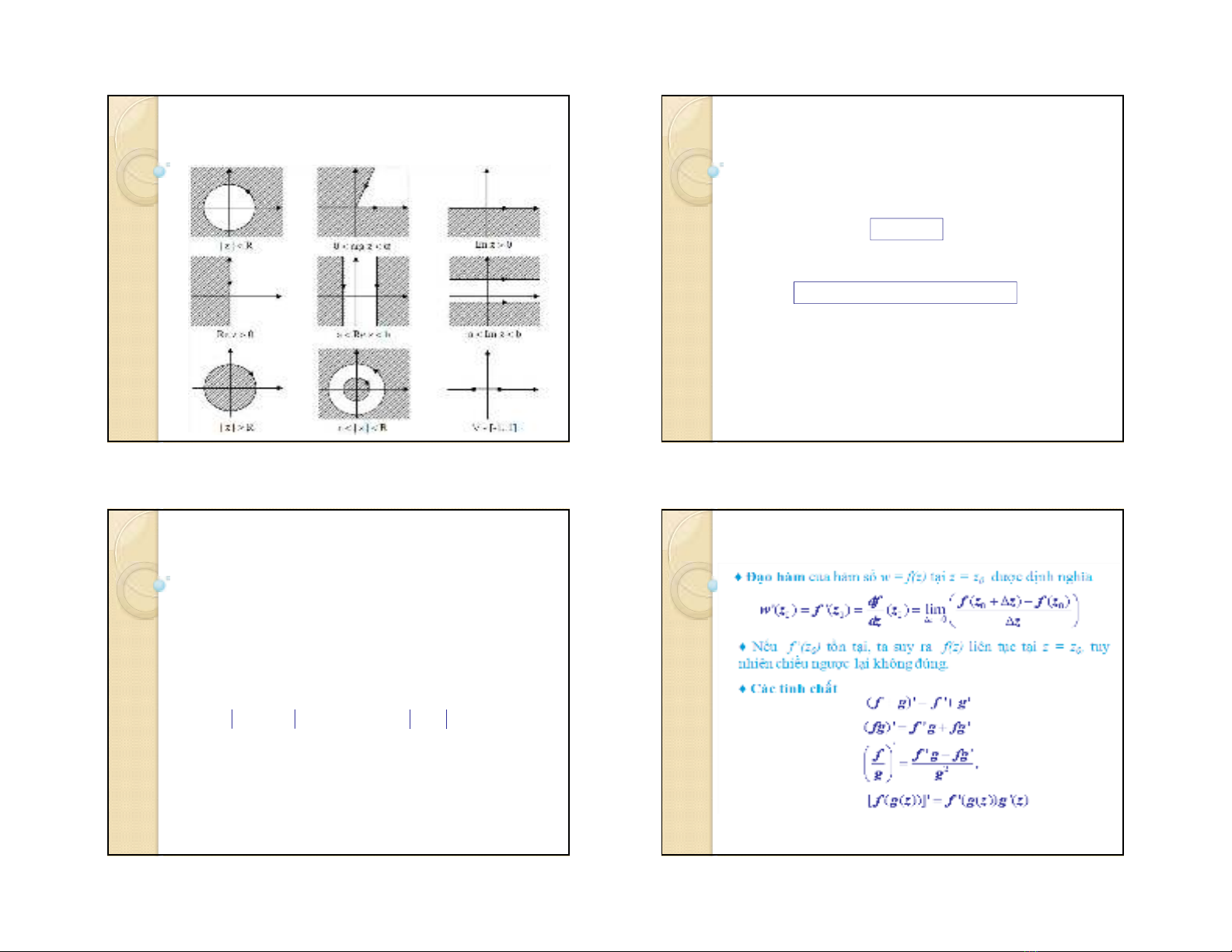
07:35
5
Một số miền đơn liên và đa liên thường gặp
17
♦Hàm biến phức: Nếu với mỗi , có tương ứng duy
nhất một số phức w(z), khi đó ta nói w(z) là một hàm của
biến phức z, được viết dưới dạng
z R
( )w f z
♦Tổng quát: f(z) có thể được viết dưới dạng
( ) ( , ) ( , ) w f z u x y iv x y
♦Ví dụ: cho w = f(z) = z
2
tìm u(x,y) và v(x,y)
222
( )
2
xwyf z z
ixy
Vậy u(x,y) = x
2
– y
2
và v(x,y) = 2xy
18
1.2. Hàm biến phức
1.3. Giới hạn và liên tục
♦Giới hạn:
Hàm số w=f(z) được xác định trong vùng lân cận z = z
0
,
ngoại trừ tại z
0
. Ta nói f(z) có giới hạn là w
0
nếu khi z → z
0
thì
f(z) → w
0
(z
0
,w
0
hữu hạn)
0
0
lim ( )
z z
f z w
nếu với mọi ε > 0 (đủ nhỏ) luôn có một δ > 0 sao cho
khi
0
( )
f z w
0
0
z z
♦Liên tục:
Hàm f(z) được gọi là liên tục tại z
0
nếu:
0
0
lim ( ) ( )
z z
f z f z
19
1.4. Đạo hàm
20