ĐồthịTrầnVĩnhĐứcHUSTNgày24tháng7năm20181/57CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tàiliệuthamkhảo▶NormanL.Biggs,DiscreteMathematics,OxfordUniversityPress,2002.2/57CuuDuongThanCong.com https://fb.com/tailieudientucntt
3/57CuuDuongThanCong.com https://fb.com/tailieudientucntt
NộidungĐồthịvàbiểudiễnMộtsốđồthịđặcbiệtĐẳngcấuBậcĐườngđivàchutrìnhCuuDuongThanCong.com https://fb.com/tailieudientucntt
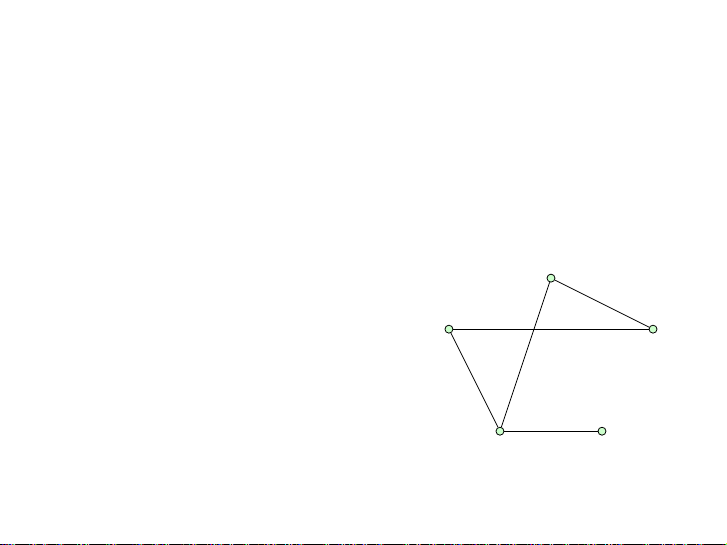
ĐịnhnghĩaMộtđồthịGlàmộtcặpcóthứtựG= (V,E),ởđâyVlàmộttập,cònElàtậpvớicácphầntửlàcáctậpconhaiphầntửcủaV.CácphầntửcủaVđượcgọilàcácđỉnh,còncácphầntửcủaEgọilàcáccạnhcủaG.VídụXétđồthịG= (V,E)trongđóV={a,b,c,d,z}
E={{a,b},{a,d},{b,z},{c,d},{d,z}}.azbdc5/57CuuDuongThanCong.com https://fb.com/tailieudientucntt