1
TOÁN R I R C Ờ Ạ
NG D NG TRONG TIN H CỨ Ụ Ọ
Gi ng viên: ả
Cao Thanh Tình (Email: tinhct@uit.edu.vn)
Bộ môn Toán Lý – ĐHCNTT – ĐHQGTPHCM
Ch ng 1. Đ i c ng v đ thươ ạ ươ ề ồ ị 2
N i dung môn h cộ ọ
Ph n 1: Lý thuy t đ thầ ế ồ ị
Đ i c ng v đ thạ ươ ề ồ ị
Các bài toán v đ ng điề ườ
Đ th ph ng và bài toán tô màu đ thồ ị ẳ ồ ị
Cây
Ph n 2: Đ i s Booleầ ạ ố
Đ i s Booleạ ố
C ng logicổ
C c ti u hóa hàm Booleự ể
Ch ng 1. Đ i c ng v đ thươ ạ ươ ề ồ ị 3
Các khái ni m c b nệ ơ ả
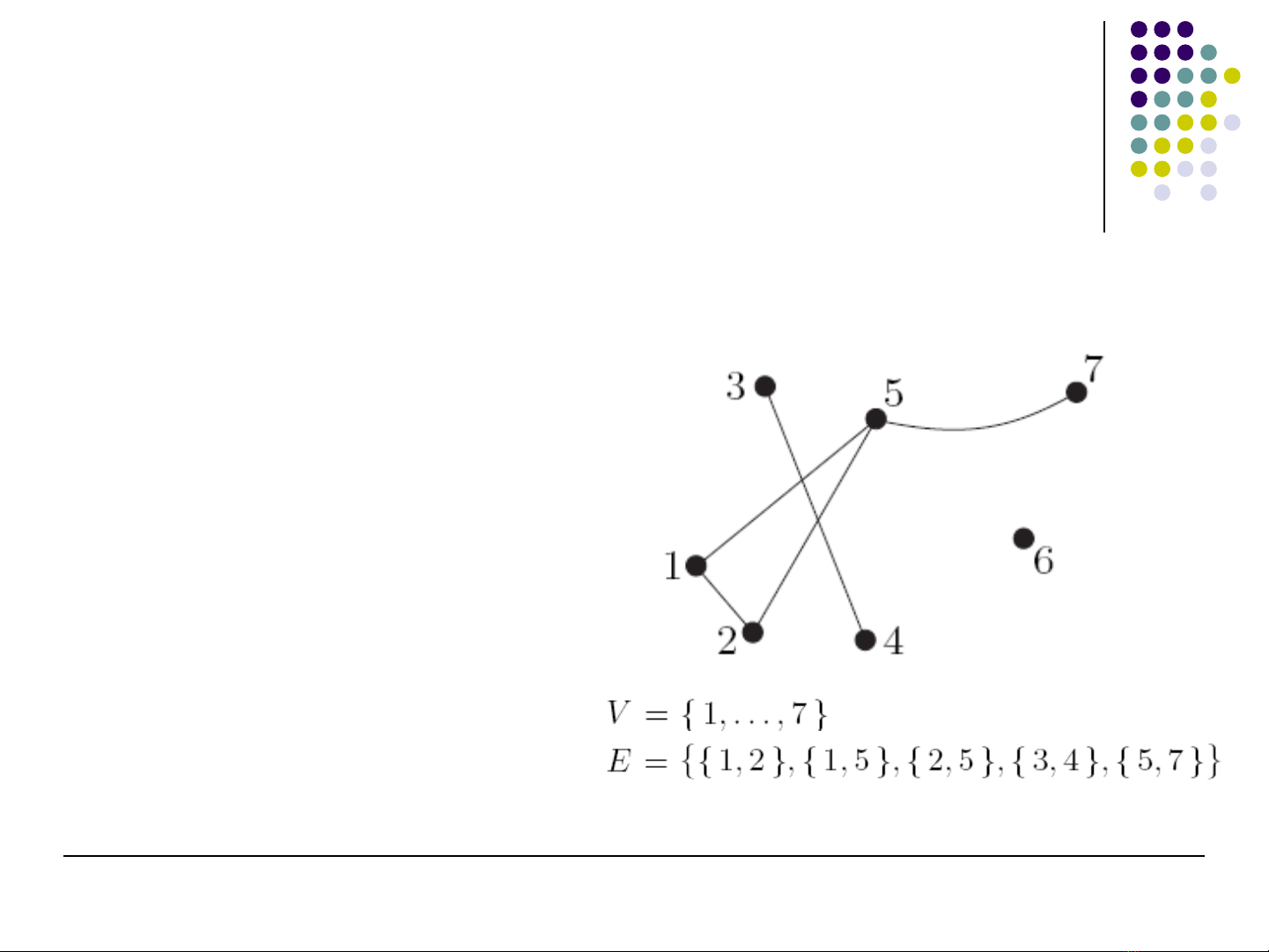
Đ th (Graph)ồ ị
G = (V, E) v i ớV≠∅
V: t p các đ nhậ ỉ
E: t p các c nh ậ ạ
C nh ạe∈E
ng v i 2 đ nh ứ ớ ỉ u, v∈V
v, w là 2 đ nh kỉ ề (hay
liên k t) v i nhau, ế ớ e liên
thu c v i ộ ớ v và w
Ký hi u: ệe = vw (…)
u ≡ v: e đ c g i là ượ ọ
vòng (khuyên) t i ạu
Ch ng 1. Đ i c ng v đ thươ ạ ươ ề ồ ị 4
Các khái ni m c b nệ ơ ả
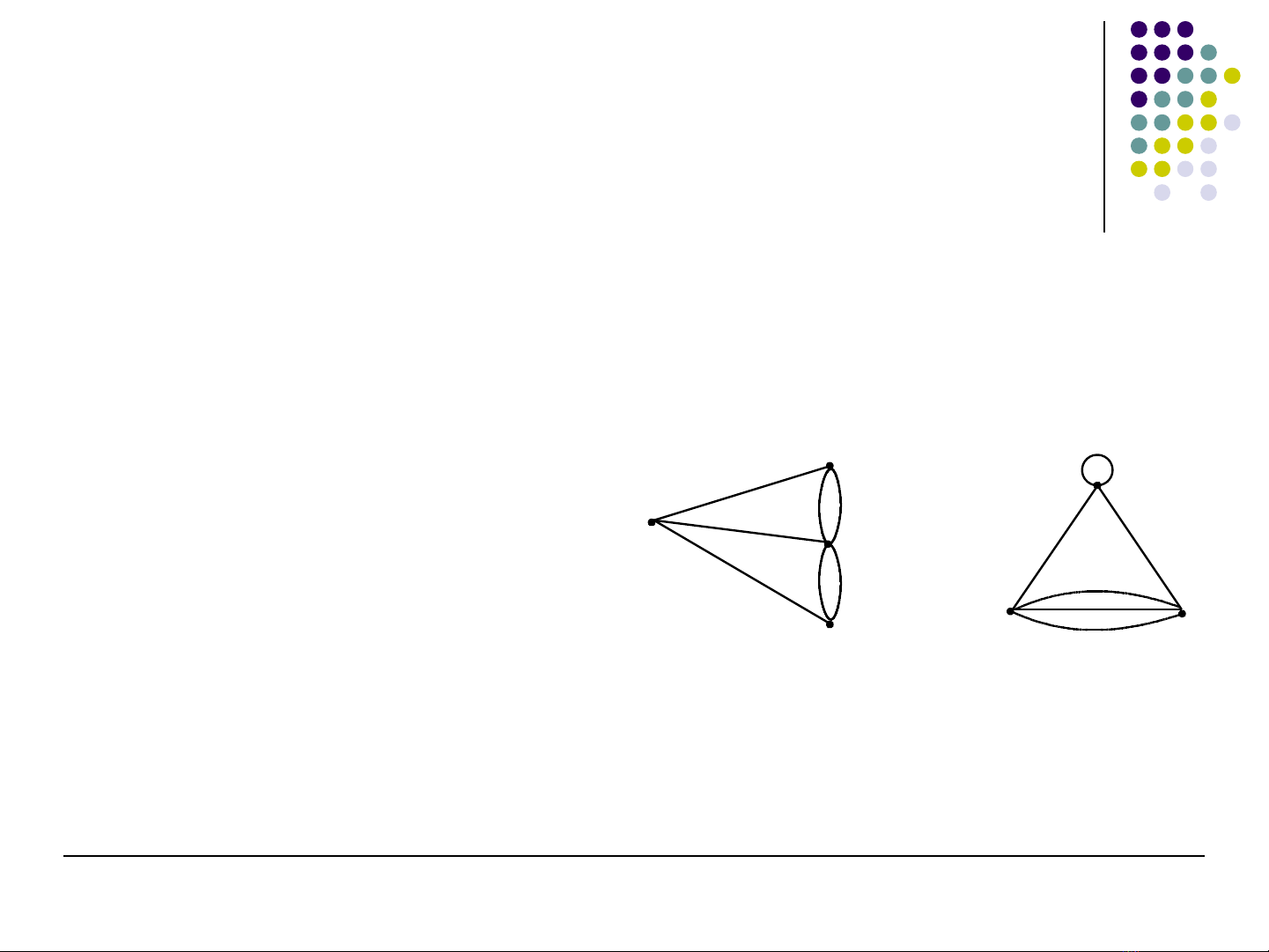
Đ th (Graph)ồ ị
C nh b iạ ộ (song song)
Hai c nh phân bi t cùng ạ ệ
t ng ng v i m t c p ươ ứ ớ ộ ặ
đ nhỉ
Đ n đ thơ ồ ị
Đ th không có vòng và ồ ị
c nh song songạ
Đa đ thồ ị
Các đ th không ph i là ồ ị ả
đ n đ thơ ồ ị
x
yz
A
B
C
D
Ch ng 1. Đ i c ng v đ thươ ạ ươ ề ồ ị 5
Các khái ni m c b nệ ơ ả
Đ th (Graph)ồ ị
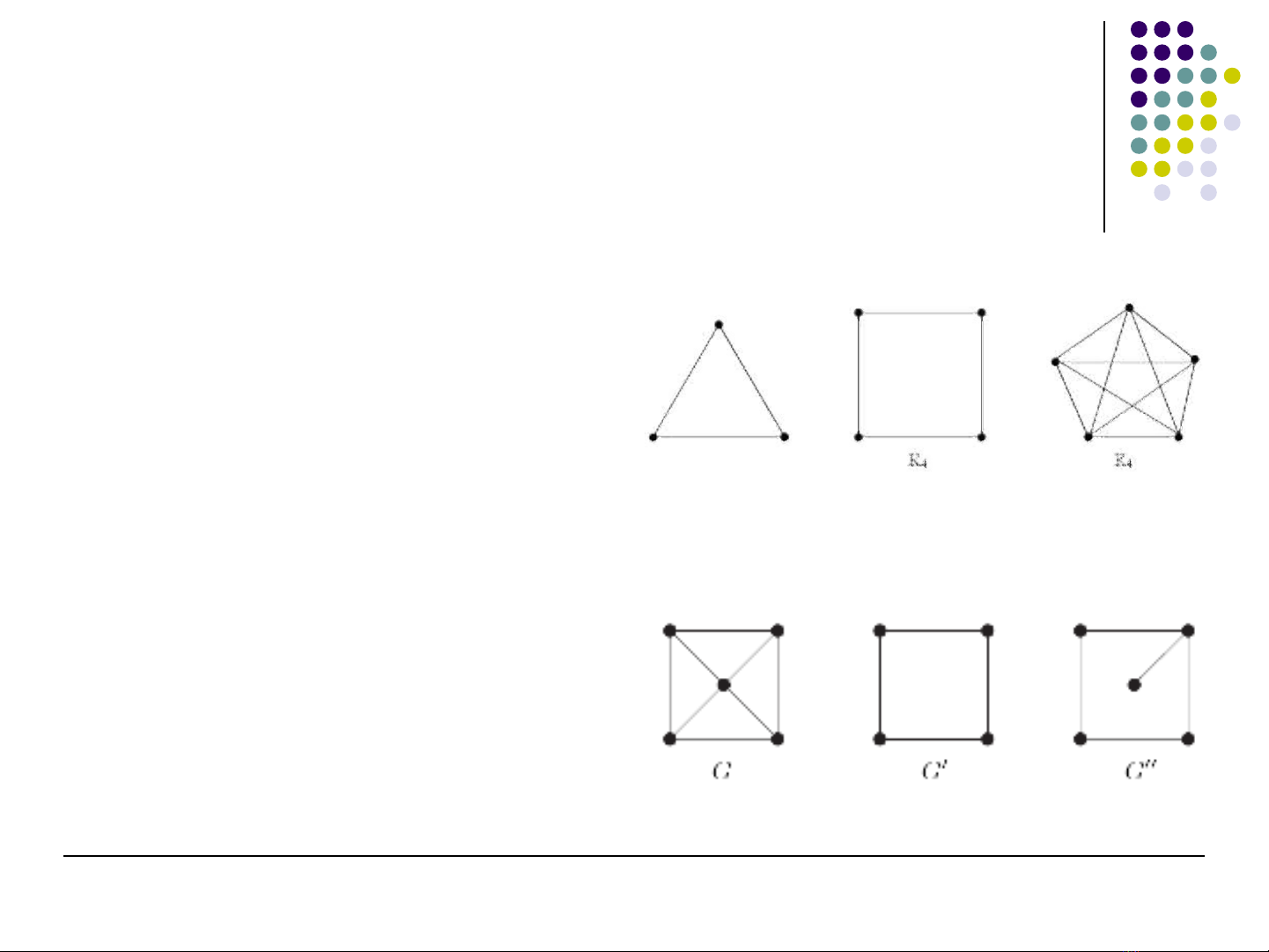
Đ th đ y đồ ị ầ ủ
Đ th mà m i c p đ nh ồ ị ọ ặ ỉ
đ u k nhauề ề
Kn: đ n đ th đ y đơ ồ ị ầ ủ
Đ th conồ ị
Đ th ồ ị G’ = (V’, E’)
V’ ⊆ V, E’ ⊆ E
Đ th h u h nồ ị ữ ạ
E và V h u h nữ ạ
Đ th vô h nồ ị ạ