PHÁÖN II :
BAÌI TÁÛP DAO ÂÄÜNG VAÌ SOÏNG CÅ
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
bµi tËp ch−¬ng 1 :
Dao ®éng tö ®iÒu hßa ghÐp
hiÖn t−îng lan truyÒn dao ®éng
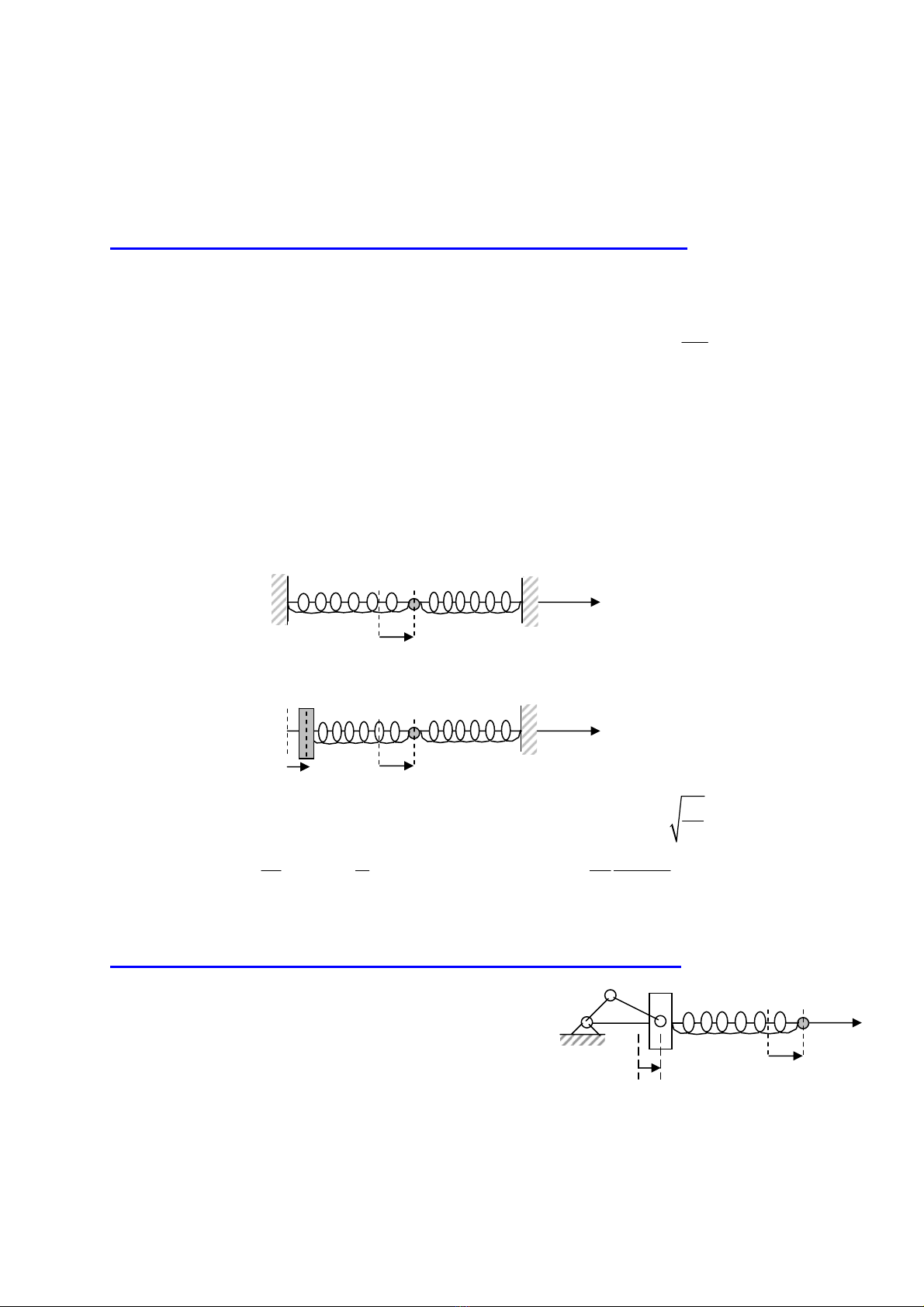
@ Bµi tËp I: Dao ®éng c−ìng bøc kh«ng cã lùc c¶n cña hÖ mét bËc tù do:
XÐt mét dao ®éng tö mét bËc tù do nh− h×nh vÏ. Hai lß xo cã cïng ®é cøng lµ K. Qu¶ cÇu cã
khèi l−îng lµ M. Gäi ()t
ψ
lµ dÞch chuyÓn cña cÇu so víi vÞ trÝ c©n b»ng. Gi¶ sö bá qua mäi
lùc c¶n t¸c dông lªn qu¶ cÇu.
1) Gi¶ sö t¹i thêi ®iÓm ban ®Çu, hÖ chÞu mét kÝch thÝch cã d¹ng: (0) 0
ψ
=
;0
0
v
t
d
dt
ψ
=
⎛⎞
=
⎜⎟
⎝⎠ . H·y
thiÕt lËp ph−¬ng tr×nh dao ®éng tù do vµ x¸c ®Þnh tÇn sè gãc
ω
cña dao ®éng tù do cña qu¶
cÇu. Suy ra biÓu thøc cña dÞch chuyÓn ()t
ψ
cña qu¶ cÇu.
2) B©y giê nhê mét c¬ cÊu tay quay con tr−ît, ®Çu A cña qu¶ cÇu chÞu mét dÞch chuyÓn d−íi
d¹ng: 0
() costt
ξ
ξω
=. H·y x¸c ®Þnh dÞch chuyÓn cña qu¶ cÇu trong chÕ ®é c−ìng bøc h×nh sin
æn ®Þnh. VÏ ®å thÞ cña biªn dé dao ®éng c−ìng bøc ()A
ω
cña qu¶ cÇu theo tÇn sè gãc cña lùc
kÝch thÝch (
ω
gäi lµ tÇn sè kÝch thÝch). øng víi gi¸ trÞ nµo cña
ω
, hiÖn t−îng céng h−ëng sÏ
x¶y ra ?
H−íng dÉn: Ph−¬ng tr×nh dao ®éng tù do cña hÖ: 2
1.
ψωψ
0
+
=
 víi 1
K
M
ω
=. DÞch chuyÓn
cña qu¶ cÇu: 0
1
1
() cos( )
2
v
tt
ψω
ω
=+
. Biªn ®é dao ®éng: 0
22
1
1
() F
AM
ω
ω
ω
=
−
víi 00
FK
ξ
=
x
()t
ξ
A
M
K
()t
ψ
K
B
x
A
M
K
()t
ψ
K
B
Céng h−ëng x¶y ra khi 1
ω
ω
=(tÇn sè kÝch thÝch
ω
b»ng tÇn sè riªng 1
ω
cña hÖ)
@ Bµi tËp II: Dao ®éng c−ìng bøc cã lùc c¶n nhít cña hÖ mét bËc tù do:
XÐt mét dao ®éng tö mét bËc tù do nh− h×nh vÏ. §Çu A
cña lß xo ®−îc kÝch thÝch bëi mét c¬ cÊu tay quay con
tr−ît, t¹o nªn mét dÞch chuyÓn cã d¹ng: 0
() costt
ξ
ξω
=
cña ®Çu A.
x
A
M
K
ψ
()t
ξ
Lß xo cã ®é cøng K b»ng h»ng sè. Qña cÇu B cã khèi
l−îng lµ M. Gäi
ψ
lµ dÞch chuyÓn cña cÇu so víi vÞ trÝ c©n
b»ng. Gi¶ sö qu¶ cÇu chÞu t¸c dông cña mét lùc c¶n nhít:
52
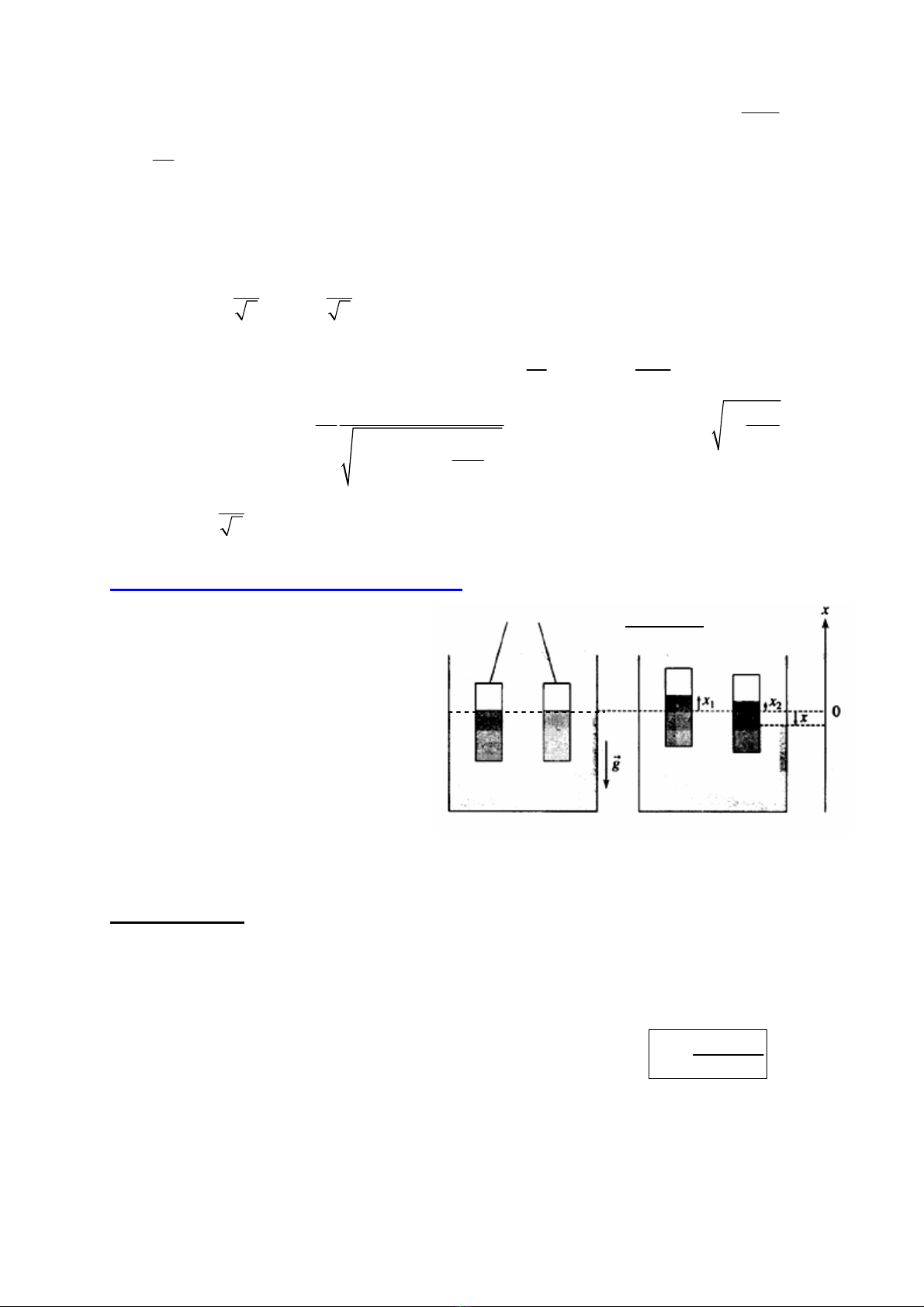
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
c
Fh
ψ
=− , trong ®ã h lµ hÖ sè c¶n nhít cña m«i tr−êng (h = h»ng sè). Gäi 1
M
Qh
ω
= víi
2
1.
K
M
ω
=(Q ®−îc gäi lµ hÖ sè phÈm chÊt)
1) ViÕt ph−¬ng tr×nh chuyÓn ®éng cña dao ®éng tö.
2) Chóng ta chØ nghiªn cøu chÕ ®é c−ìng bøc h×nh sin æn ®Þnh. H·y x¸c ®Þnh biªn ®é dao
®éng c−ìng bøc ()A
ω
cña dao ®éng tö nãi trªn, b»ng c¸ch biÓu diÔn ()t
ψ
vµ () . ()Ft K t
ξ
=
d−íi d¹ng phøc. Kh¶o s¸t sù biÕn thiªn cña ()A
ω
theo tÇn sè gãc
ω
cña lùc kÝch thÝch trong
tr−êng hîp 1
2
Q> vµ 1
2
Q<. Tõ ®ã suy ra ®iÒu kiÖn ®Ó cã céng h−ëng vµ gi¸ trÞ cña
ω
khi x¶y ra céng h−ëng.
H−íng dÉn: Ph−¬ng tr×nh dao ®éng tù do cña hÖ: 2
1
1
()
.Ft
QM
ω
ψψωψ
++=
 víi () ()Ft K t
ξ
=.
Biªn ®é dao ®éng:
()
0
2
2
22 1
1
1
() F
AM
Q
ω
ωω
ωω
=
⎛⎞
−+
⎜⎟
⎝⎠
. ()A
ω
cùc ®¹i khi 12
1
12Q
ωω
=− víi
®iÒu kiÖn 1
2
Q> (®iÒu kiÖn ®Ó cã céng h−ëng).
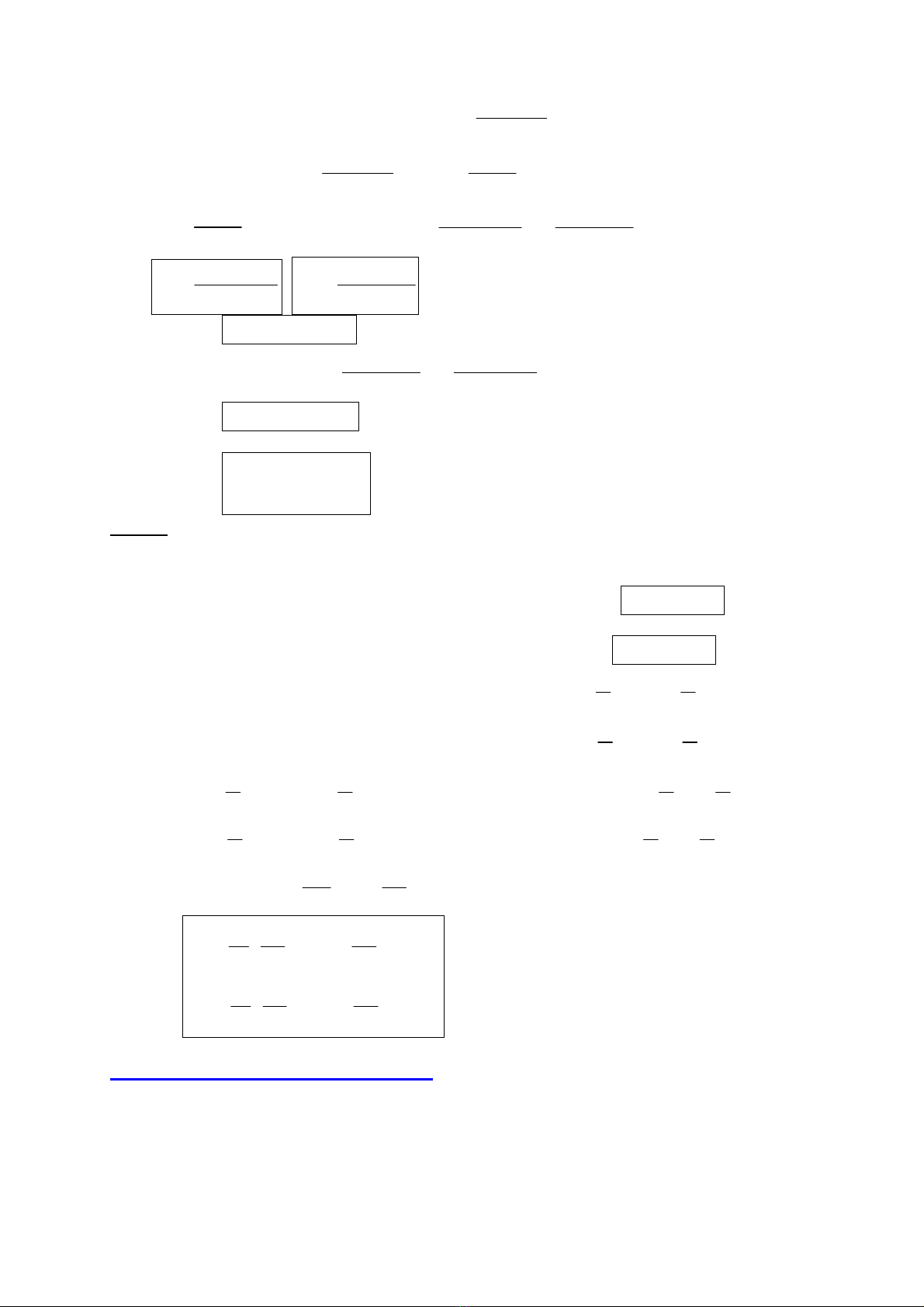
@ Bµi 1 (Trang 28): Dao ®éng cña hai phao:
Hai phao h×nh trô gièng nhau (tiÕt diÖn s
vµ khèi l−îng m) cã thÓ dao ®éng trong
n−íc cña mét b×nh chøa cã tiÕt diÖn S.
Gäi ρ lµ khèi l−îng riªng cña n−íc. VÞ
trÝ cña c¸c phao ®−îc x¸c ®Þnh b»ng c¸c
dÞch chuyÓn x1 vµ x2 cña chóng theo
ph−¬ng th¼ng ®øng so víi vÞ trÝ c©n b»ng.
1) T×m hÖ ph−¬ng tr×nh vi ph©n m« t¶
chuyÓn ®éng cña hai phao (thõa nhËn
r»ng mÆt tho¸ng cña n−íc n»m ngang vµ
cã thÓ ¸p dông ®Þnh lý ArchimÌde).
2) Gi¶i hÖ ph−¬ng tr×nh trªn, gi¶ sö r»ng
t¹i thêi ®iÓm ban ®Çu, hai phao ®Òu n»m
ë vÞ trÝ c©n b»ng, víi vËn tèc ban ®Çu lµ
2v0 ®èi víi phao thø nhÊt vµ v0 ®èi víi phao thø hai.
TiÕt diÖn S
TiÕt diÖn S
TiÕt diÖn s H×nh bµi 1
Bµi gi¶i : C©u 1 :
¾ Khi phao dÞch chuyÓn theo ph−¬ng th¼ng ®øng ⇒ mùc n−íc trong b×nh bÞ thay ®æi.
Gäi x lµ dÞch chuyÓn cña mÆt tho¸ng chÊt láng so víi vÞ trÝ lóc c¸c phao c©n b»ng; x1 vµ x2 lµ
dÞch chuyÓn cña hai phao so víi vÞ trÝ c©n b»ng.
Khi hai phao næi lªn so víi vÞ trÝ c©n b»ng (x1 > 0, x2 > 0), mùc n−íc trong b×nh sÏ h¹ xuèng :
x < 0.
Do thÓ tÝch n−íc trong b×nh kh«ng ®æi, nªn : 12
( ).-(-2)
x
xs xS s
+
= ⇒ 12
()
2
x
xs
xSs
+
=− −
¾ ¸p dông ®Þnh lý vÒ ®éng l−îng cho c¸c phao :
10,1
20,2
()
()
chim
chim
mx mg V x x s g
mx mg V x x s g
ρ
ρ
⎧⎡⎤
=− + − −
⎪⎣
⎨⎡⎤
=− + − −
⎪⎣⎦
⎩


⎦
mg
Víi : V0, chim : thÓ tÝch phÇn ch×m trong n−íc cña mçi phao lóc phao c©n b»ng : Vg
0,chim
ρ
=
53
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Suy ra : víi :
11
22
() (1
() (
mx x x s g
mx x x s g
ρ
ρ
=− −
⎧
⎨=− −
⎩


)
2)
12
()
2
x
xs
xSs
+
=−
−
Tõ (1) suy ra :
()
12
11 1 11
() 2
22
xxs sg
mx x s g x S sx sx sx
Ss Ss
ρ
ρ
+
⎛⎞
=− + =− − + +
⎜⎟
−−
⎝⎠
 2
⇒
[]
112
()
2
sg
mx x S s sx
Ss
ρ
=− − +
−

() ()
2
112
()
22
sgS s s g
x
xx
mS s mS s
ρρ
−
=− −
−−

⇒
§Æt :
()
2
1
()
2
sgS s
mS s
ρ
ω
−
=−;
()
2
2
12 2
sg
mS s
ρ
ω
=− (Chó ý r»ng : 12
ω
ω
>)
Suy ra : 22
11122
x
x
ωω
=− −
 x
T−¬ng tù, tõ (2) suy ra :
() ()
2
21
()
22
sg sgSs
2
x
xx
mS s mS s
ρρ
−
=− −
−−

Hay : 22
22112
x
x
ωω
=− −
 x
¾ Tãm l¹i, hÖ ph−¬ng tr×nh vi ph©n m« t¶ chuyÓn ®éng cña hai phao :
22
1112
22
2211
2
2
x
xx
x
xx
ωω
ωω
⎧=− −
⎪
⎨=− −
⎪
⎩

 (3)
C©u 2 :
¾ Céng vÕ theo vÕ cña hÖ ph−¬ng tr×nh (3) :
22 2 2
1 2 11 1 2 22 21
x
xxxxx
ω
ωωω
+=− − − −
  ⇒ 22
12 112 212
()()
x
xxxx
ωω
+=− + − +
  x
)
⇒ 22
12 1 212
()(
x
xxx
ωω
+=− + +
  2
12 112
() ⇒
x
xxx+=−Ω +
  2
2
víi 22
11
ω
ω
Ω
=+
T−¬ng tù, trõ vÕ theo vÕ cña hÖ ph−¬ng tr×nh (3) :
22
12 1 212
()()
x
xxx
ωω
−=− − −
  2
12 212
() ⇒
x
xxx−=−Ω −
  2
2
víi 22
21
ω
ω
Ω
=−
Suy ra :
2
12 112
2
12 212
()
()
x
xxx
x
xx
⎧+=−Ω +
⎪
⎨−=−Ω −
⎪
⎩
 
  x
⇒ 12 1
12 2
sin
sin
x
xA t
x
xB
⎧
t
+
=Ω
⎪
⎨
−
=Ω
⎪
⎩
⇒
11
21
sin sin
22
sin sin
22
AB
2
2
x
tt
AB
x
tt
⎧
=
Ω+ Ω
⎪
⎪
⎨
⎪
=
Ω− Ω
⎪
⎩
Ta cã : 11 1 2 2
cos cos
22
AB
x
tt=Ω Ω +Ω Ω
. T¹i t = 0, 10
2vx
=
⇒ 01 2
2v 22
A
B
=Ω +Ω (4)
Ta cã : 21 1 2 2
cos cos
22
AB
x
tt=Ω Ω −Ω Ω
. T¹i t = 0, 2
vx0
=
⇒ 01 2
v22
A
B
=Ω −Ω (5)
Tõ (4) vµ (5), suy ra : 0
1
3v
=AΩ; 0
2
v
=B
Ω
Tãm l¹i :
0
11
12
0
21
12
v3 1
sin sin
2
v31
sin sin
2
2
2
x
tt
x
tt
⎧⎛⎞
=Ω+
⎪⎜⎟
ΩΩ
⎪⎝
⎨⎛⎞
⎪=Ω−
⎜⎟
⎪ΩΩ
⎝⎠
⎩
Ω
⎠
Ω
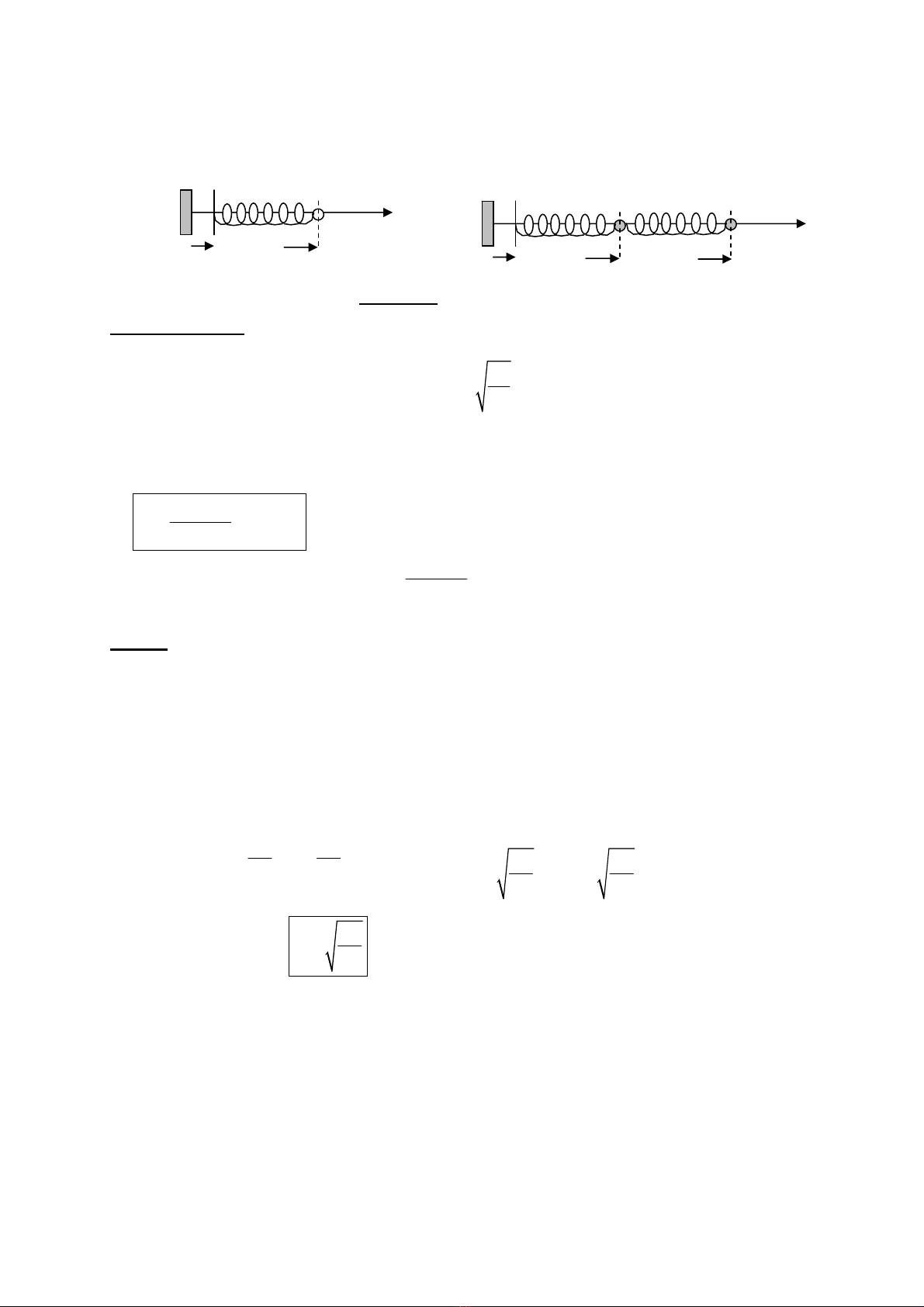
@ Bµi 2 (Trang 28): TriÖt tiªu dao ®éng:
XÐt dao ®éng tö nh− trªn h×nh vÏ (h×nh a). DÞch chuyÓn cña ®Çu A cña lß xo cã d¹ng h×nh sin:
(gi¶ sö ).
0
() sinyt y t=Ω 2
11
Km≠Ω
1) X¸c ®Þnh dÞch chuyÓn x1(t) cña dao ®éng tö so víi vÞ trÝ c©n b»ng trong chÕ ®é c−ìng bøc
h×nh sin æn ®Þnh.
54
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
2) Mét dao ®éng tö thø 2 ®−îc ®Æt nèi tiÕp dao ®éng tö trªn, nh− s¬ ®å trªn h×nh vÏ (h×nh b).
§Çu A cña lß xo thùc hiÖn dÞch chuyÓn h×nh sin nh− ®· nãi trªn ®©y. Víi c¸c ®iÒu kiÖn nµo
cña K2 vµ m2, dÞch chuyÓn x1 trong chÕ ®é c−ìng bøc æn ®Þnh sÏ b»ng 0 ?
x
()yt
A1
m
1
K
1()
x
t
(a) (b)
H×nh bµi 2
x
()yt
A1
m
1
K
1()
x
t
2
K2
m
2()
x
t
Bµi gi¶i : C©u 1 :
Ph−¬ng tr×nh chuyÓn ®éng cña khèi l−îng m1 cã d¹ng :
11 1 1
()mx x y K=− −
 ⇒ 2
111 1
2
x
xy
ω
ω
+=
 víi 1
1
1
K
m
ω
= ⇒ 22
111 10
sin
x
xy
ωω
t
+
=Ω
 (1)
NghiÖm riªng x1(t) cña ph−¬ng tr×nh (1) biÓu diÔn dao ®éng c−ìng bøc cña khèi l−îng m1 cã
d¹ng : 1() ( )sin
x
tA=Ω Ωt
⇒ 1cos
x
At=Ω Ω
⇒ 22
11
sin
x
At x
=
−Ω Ω = −Ω

Thay tÊt c¶ vµo (1) : 22 2
111 10
sin
x
xy
ωω
t+ = Ω−Ω ⇒ 22 2
1110
() sin
x
yt
ωω
−
Ω= Ω
⇒
2
1
10
22
1
sin
x
yt
ω
ω
=Ω
−Ω
Biªn ®é dao ®éng c−ìng bøc :
2
10
2
1
() y
A
ω
ω
Ω= 2
−
Ω. Céng h−ëng x¶y ra khi : 1
ω
Ω= , khi ®ã |A|
→ ∞
C©u 2 :
Ph−¬ng tr×nh chuyÓn ®éng cña hÖ hai dao ®éng tö liªn kÕt m1, m2 :
11 1 1 2 2 1
22 2 2 1
()(
()
mx K x y K x x
mx K x x
=− − + −
⎧
⎨=− −
⎩


)
2
Khi x1 = 0, ph−¬ng tr×nh trªn trë thµnh :
12
22 22
0Ky Kx
mx Kx
=+
⎧
⎨=−
⎩ (2)
NghiÖm riªng x2 cña ph−¬ng tr×nh (2) biÓu diÔn chÕ ®é c−ìng bøc æn ®Þnh cña khèi l−îng m2
cã d¹ng :
11
20
22
22
sin
sin
KK
x
yy
KK
xA t
⎧=− =− Ω
⎪
⎨
⎪=Ω
⎩
t
víi : 2
2
2
K
m
Ω= ⇒ 2
2
K
m
Ω=
Nh− vËy, víi ®iÒu kiÖn 2
2
K
m
Ω= th× dÞch chuyÓn x1(t) trong chÕ ®é c−ìng bøc æn ®Þnh tháa
m·n x1(t) = 0. HÖ lß xo nh− trªn ®−îc øng dông vµo viÖc thiÕt kÕ hÖ thèng c¸ch rung trong kü
thuËt.
55