Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Bµi tËp ch−¬ng 2 :
d©y rung - ph−¬ng tr×nh ®al¨mbe
@ ¸p dông 1: D©y Melde (Trang 48)
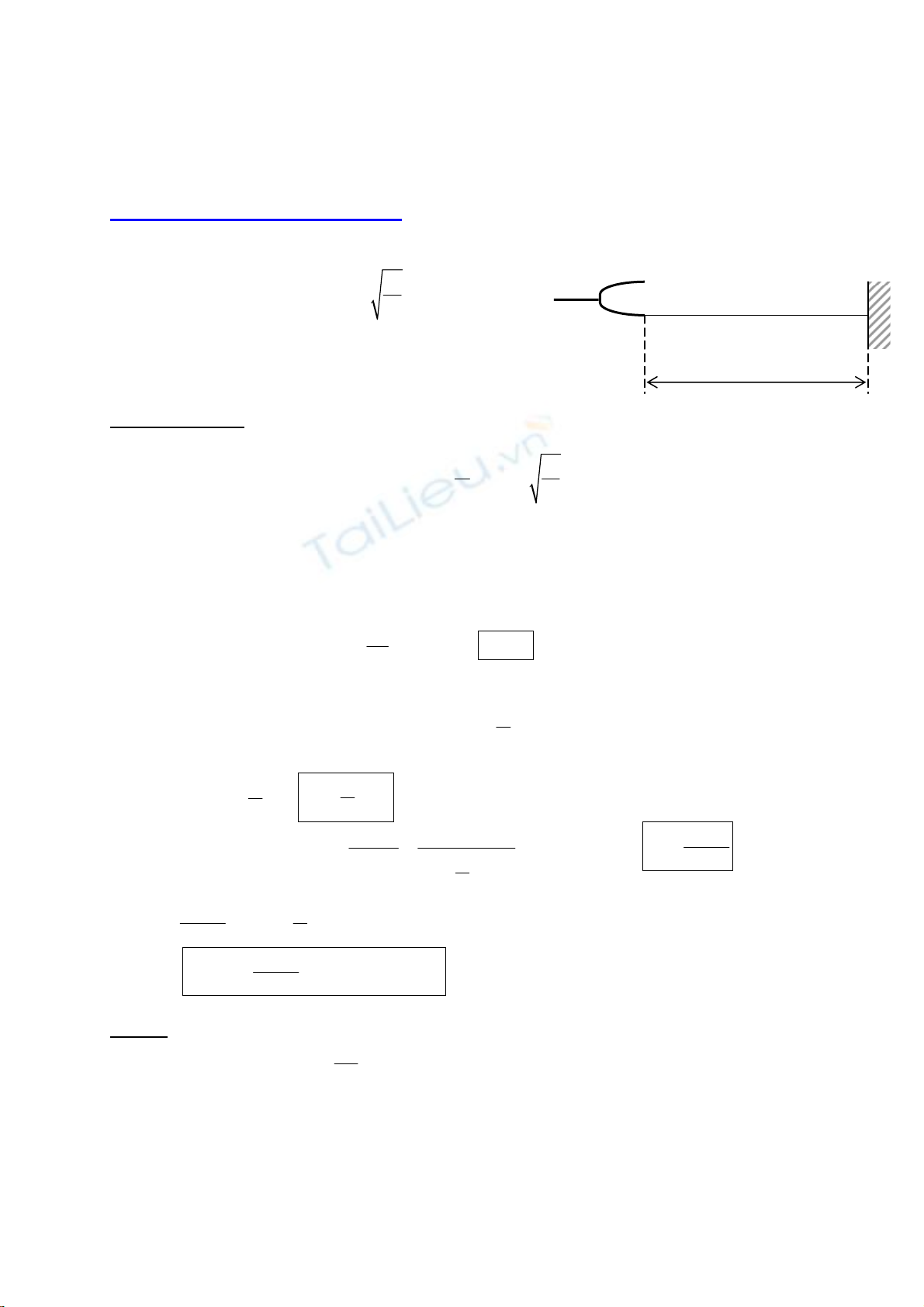
Trong thÝ nghiÖm vÒ d©y Melde, thanh rung thùc hiÖn c¸c dao ®éng h×nh sin cã biªn ®é a:
ψ(0,t) = acosωt. Sîi d©y cã chiÒu dµi L, ®Çu kia cè ®Þnh.
Løc c¨ng cña sîi d©y b»ng T0 ( 0
T
c
µ
=) .
©m thoa
A B
L
1) X¸c ®Þnh dÞch chuyÓn ψ(x,t) t¹i mét ®iÓm M bÊt kú
trªn d©y, t¹i mét thêi ®iÓm t bÊt kú.
2) Gi¶i thÝch vµ b×nh luËn hiÖn t−îng céng h−ëng. X¸c
®Þnh gi¸ trÞ cña c¸c tÇn sè céng h−ëng.
Bµi gi¶i : C©u 1 :
NghiÖm sãng dõng h×nh sin cã d¹ng :
0
(,) cos( )cos( )
FG
xt kx t
ψ
ψϕω
=+ +
ϕ
víi kc
ω
=
vµ 0
T
c
µ
=.
§iÒu kiÖn biªn : (0, ) cos
(,) 0
ta
Lt
t
ψ
ω
ψ
=
⎧
⎨=
⎩
Suy ra :
0
0
(0, ) cos cos( ) cos (1)
(,) cos( )cos( ) 0 (2)
FG
FG
tta
Lt kL t
ψψϕωϕ ω
ψψ ϕωϕ
=+=
⎧
⎨=+ +=
⎩
t
Tõ (1) : 0cos Fa
ψ
ϕ
=⇒
0
cos F
a
ϕ
ψ
= (3) vµ : 0
G
=
Tõ (2) : 0cos( )cos 0
F
kL t
ψ
ϕω
+= co
⇒s( ) 0
F
kL
ϕ
+
= (4)
(Ghi chó : gi¸ trÞ cos t
ω
cã thÓ b»ng 0 khi 2
tk
π
ω
π
=+ nh−ng v× xÐt víi mäi t nªn ph¶i
cã cos 0t
ω
≠)
Tõ (4) : 2
F
kL
π
ϕ
+=
⇒ 2
FkL
π
ϕ
=−
Tõ (3) : 0cos cos 2
F
aa
kL
ψ
π
ϕ
==
⎛⎞
−
⎜⎟
⎝⎠
⇒0sin
a
kL
ψ
= ⇒
(,) cos( )cos
sin 2
a
x
tkxkL
kL t
π
ψ
ω
=+−
Tãm l¹i : (,) sin[( )]cos
sin
a
x
tkLx
kL t
ψ
ω
=−
(5)
(Ghi chó : NÕu mÉu sè sinkL = 0, ta cã tr−êng hîp céng h−ëng)
C©u 2 :
Ta thÊy r»ng, khi n
n
kk
L
π
== hay n
kL n
π
=
víi n nguyªn th× sin ψ(x,t) trªn
lý thuyÕt b»ng v« cïng ⇒ d©y bÞ céng h−ëng.
0
n
kL= ⇒
Thùc tÕ, do sù t¾t chÊn kh«ng thÓ tr¸nh khái, ®ång thêi ®é cøng cña d©y (mµ ta bá qua khi
thiÕt lËp ph−¬ng tr×nh truyÒn sãng §al¨mbe), kh«ng cßn cã thÓ bá qua khi cã céng h−ëng
biªn ®é cña c¸c dÞch chuyÓn cña d©y lµ giíi néi.
⇒
(Khi céng h−ëng, a rÊt bÐ so víi biªn ®é t¹i c¸c bông dao ®éng ⇒ ®Çu d©y g¾n víi thanh
rung cã thÓ coi nh− lµ mét nót dao ®éng).
66
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Ta cã, tÇn sè dao ®éng riªng cña d©y : nn
kc
ω
=
víi n
n
k
L
π
=⇒ n
nc
L
π
ω
=
⇒ C¸c tÇn sè céng h−ëng: 22
n
n
nc
L
ω
ν
π
==
Tõ (5) suy ra chu kú theo kh«ng gian λn cña ψ(x,t) (b−íc sãng λn) : 2
n
n
k
π
λ
=
Khi d©y bÞ céng h−ëng th× n
n
kk
L
π
== ⇒2
n
L
n
λ
=⇒ 2n
n
L
λ
=
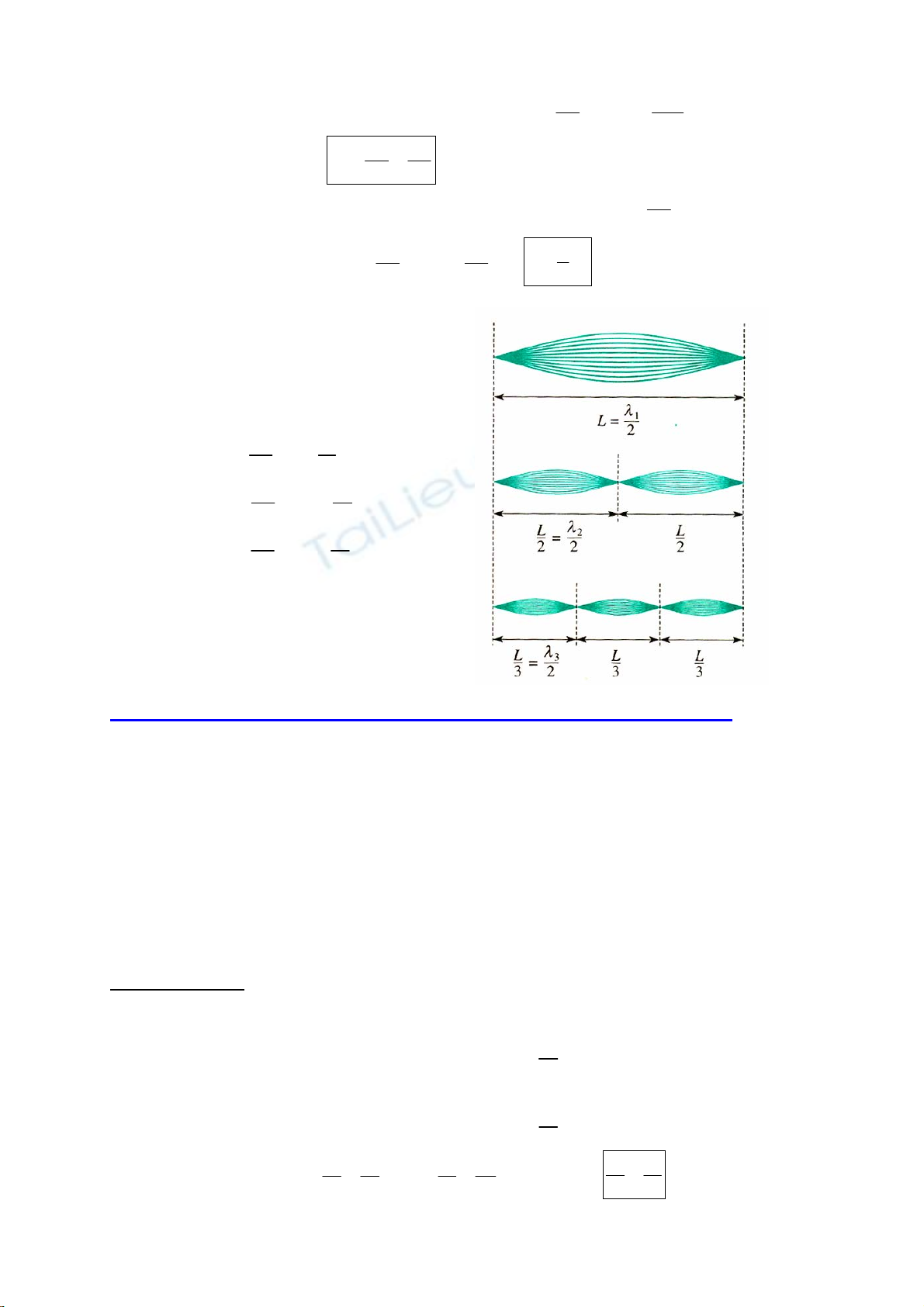
Víi n = 1 ⇒12
c
L
ν
=; 1
2
L
λ
=
Víi n = 2 ⇒2
2
2
c
L
ν
=; 2
22
L
λ
=
Víi n = 3 ⇒3
3
2
c
L
ν
=; 3
32
L
λ
=
@ ¸p dông 2: Nghiªn cøu c¸c d¹ng dao ®éng riªng cña mét sîi d©y (Trang 52)
Khi thÝ nghiÖm víi d©y Melde, ng−êi ta nhËn thÊy c¸c kÕt qu¶ sau ®©y :
1) Víi cïng mét chiÒu dµi L cña sîi d©y vµ víi cïng mét khèi l−îng M m¾c vµo nã, ng−êi ta
thu ®−îc c¸c kÕt qu¶ sau:
TÇn sè céng h−ëng lµ 19 Hz khi cã hai bã sãng.
TÇn sè céng h−ëng lµ 28 Hz khi cã ba bã sãng.
a) C¸c gi¸ trÞ b»ng sè nãi trªn t−¬ng thÝch nhau hay kh«ng ?
b) C¸c tÇn sè céng h−ëng kÕ tiÕp sÏ b»ng bao nhiªu ?
2) ChiÒu dµi sîi d©y lµ L = 117cm. VËn tèc truyÒn sãng dao ®éng trªn d©y nµy b»ng bao
nhiªu ?.
3) Khèi l−îng M m¾c vµo d©y b»ng M = 25g.
a) Søc c¨ng cña sîi d©y b»ng bao nhiªu ?
b) Rót ra cì ®é lín cña khèi l−îng trªn mét ®¬n vÞ chiÒu dµi cña sîi d©y.
Bµi gi¶i : C©u 1 :
a) Trªn d©y Melde, khi thÝ nghiÖm nhËn thÊy :
- víi tÇn sè céng h−ëng 19Hz th× cã hai bã sãng
⇒ TÇn sè riªng cña d©y : 219Hz
ν
=, chiÒu dµi d©y 2
22
L
λ
=
- víi tÇn sè céng h−ëng 28Hz th× cã ba bã sãng
⇒ TÇn sè riªng cña d©y : 328Hz
ν
=, chiÒu dµi d©y 3
32
L
λ
=
Víi c¸c kÕt qu¶ trªn, ta cã : 219 9,5
22
ν
=≈ ; 328 9,3
33
ν
=≈ tøc lµ : 3
2
23
ν
ν
≈
67
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
C¸c gi¸ trÞ b»ng sè nãi trªn lµ t−¬ng thÝch víi nhau bëi v× theo lý thuyÕt ®· häc, ta cã :
0nn
ν
ν
= hay : 0
n
n
ν
ν
= tøc lµ : 3
20
...
22
ν
ν
ν
===
Nh− vËy : 3
2
09,4
23 Hz
ν
ν
ν
==≈
b) C¸c tÇn sè céng h−ëng kÕ tiÕp :
40
4 4.9,4 37,6Hz
ν
ν
== = ; 09,4.
nnn
ν
ν
==
C©u 2 :
¾ ChiÒu dµi d©y : L = 117cm.
Mµ : 2
n
c
n
L
ν
= ⇒ VËn tèc truyÒn sãng d©y : 22.117.9,4 2200 /
n
L
cc
nms
ν
== ≈ ⇒
22 /cm=s
(Ghi chó : Cã thÓ tÝnh theo c¸ch kh¸c nh− sau :
Ta cã :2
n
L
n
λ
=
⇒
2
nnL
λ
=
⇒
01.2.1,17m
λ
=
⇒
02,34m
λ
=
MÆt kh¸c : c00 nn
λ
νλν
==
⇒
c00 2,34.9,4
nn
λ
νλν
=== s
⇒
22 /cm
=
C©u 3 :
a) Søc c¨ng trªn d©y : T0 = Mg
Víi : M = 25g ⇒ T0 = 25.10-3.10N ⇒ T0 = 0,25N
b) VËn tèc truyÒn sãng c b»ng : 0
T
c
µ
= ⇒ Khèi l−îng mét ®¬n vÞ chiÒu dµi cña
d©y :0
22
0,25
(22)
T
c
µ
== ⇒ 41
5,2.10 0,52 /Kgm g m
µ
−−
≈=
(víi ®é chÝnh x¸c cña phÐp ®o tÇn
sè).
@ Bµi 2, trang 57, ¶nh huëng cña ®é cøng cña mét sîi d©y ®Õn tÇn sè dao ®éng cña nã :
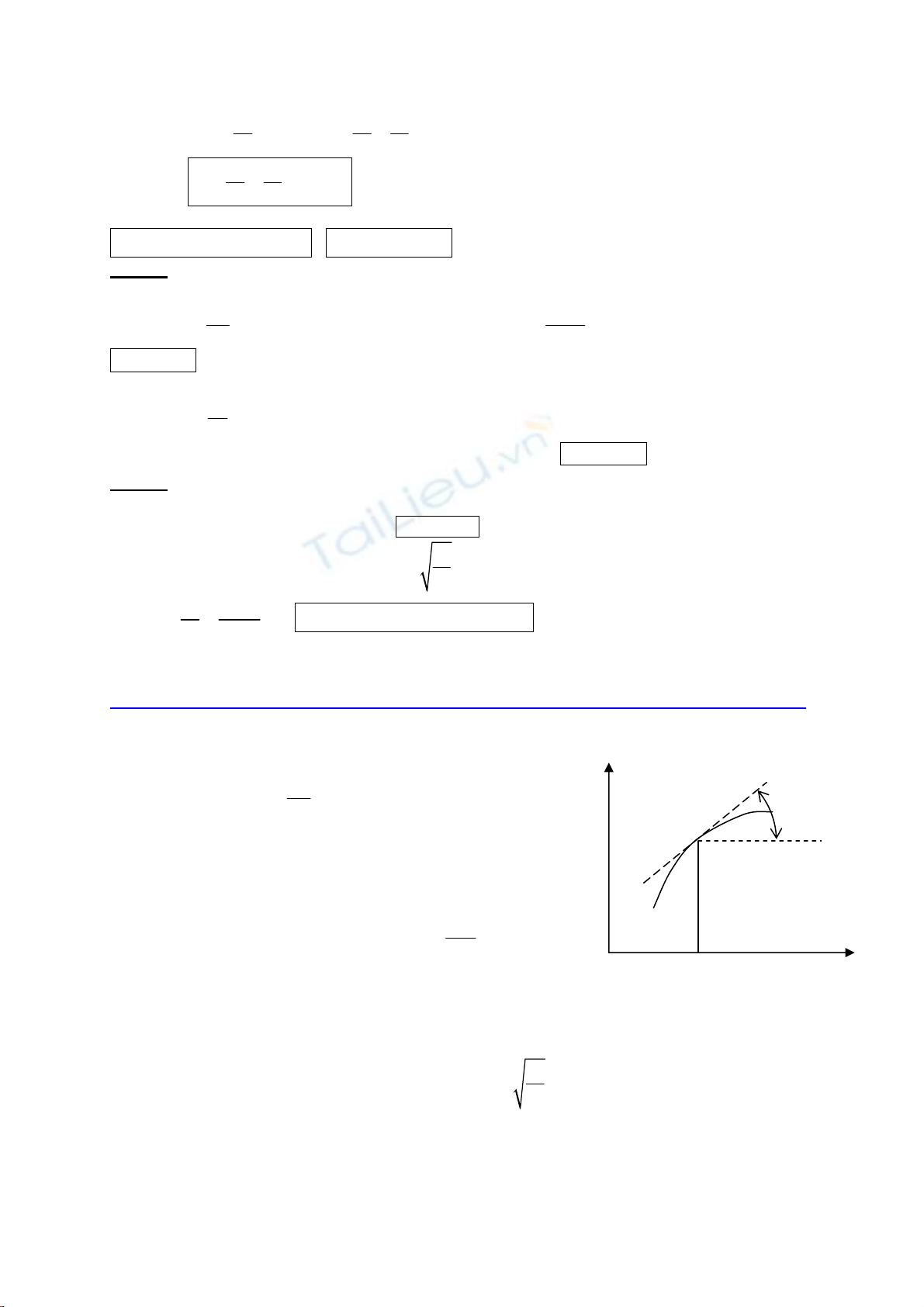
Mét sîi d©y, khèi l−îng trªn mét ®¬n vÞ chiÒu dµi lµ µ,
chiÒu dµi L, ®−îc cè ®Þnh ë hai ®Çu, chÞu mét lùc c¨ng d©y
T0, dao ®éng ë d¹ng dao ®éng riªng thø n theo quy luËt:
y
x
α
dx
x
(,) cos sin
n
x
xt A t n
L
π
ψω
= víi n lµ sè nguyªn.
Víi c¸c tÇn sè cao, ph¶i kÓ ®Õn ¶nh h−ëng cña ®é cøng cña
d©y. Trong biÓu thøc c©n b»ng lùc t¸c dông lªn mét ph©n tè
d©y cã chiÒu dµi dx, cÇn ®−a thªm mét lùc bæ sung dR
G
cã
xu h−íng chèng l¹i sù uèn cong cña d©y. H×nh chiÕu cña lùc
nµy lªn trôc (Oy) ®−îc viÕt thµnh :
3
3.
y
dR dx
x
α
γ
∂
=−
∂
O
Trong ®ã γ lµ mét h»ng sè phô thuéc vµo vËt liÖu sîi d©y.
1) H·y tÝnh tØ sè ε gi÷a mo®un cña vµ mo®un cña thµnh
phÇn trªn trôc (Oy) cña hîp lùc c¨ng d©y t¸c dông lªn ph©n tè d©y cã chiÒu dµi dx.
y
dR
2) ¸p dông hÖ thøc c¬ b¶n cña ®éng lùc häc cho ph©n tè d©y cã chiÒu dµi dx.
Tõ ®ã suy ra tÇn sè dao ®éng n
ω
cña sîi d©y theo 0
T
c, L, ε vµ n.
µ
=
3) TÝnh ®é hiÖu chØnh t−¬ng ®èi cña tÇn sè g¾n víi d¹ng dao ®éng riªng n, xuÊt hiÖn do kÓ
®Õn ¶nh h−ëng cña ®é cøng cña d©y (gi¶ sö ε <<1). ¸p dông b»ng sè cho n = 1; n = 2 vµ
n = 10.
Cho biÕt: L = 0,5m; T = 387 N;
γ
= 10-2 N.m2.
68
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Bµi gi¶i : C©u 1 :
Khi d©y kh«ng cã ®é cøng, thµnh phÇn trªn trôc Oy cña hîp lùc c¨ng d©y t¸c dông lªn ph©n
tè d©y dx (xem l¹i phÇn lý thuyÕt) :
[]
2
00
2
(,)(,)
y
FT xdxt xt T dxT dx
xx
αψ
αα
∂∂
=+−= =
∂∂
0
Suy ra :
34
34
2
0
02
y
y
dx dx
dR xx
RT
Tdx dx
xx
αψ
γγ
εαψ
∂∂
∂∂
== =
∂∂
∂∂
⇒
4
4
2
02
x
T
x
ψ
γ
ε
ψ
∂
∂
=∂
∂
(1)
(L−u ý r»ng :
2
2
;
x
xx
ψ
αψ
α
∂∂ ∂
==
∂∂ ∂
)
C©u 2 :
¾ ¸p dông hÖ thøc c¬ b¶n cña ®éng lùc häc (®Þnh luËt II Newton) cho ph©n tè d©y dx vµ
chiÕu lªn trôc Oy, ta cã :
2
2y
dx F dR
t
ψ
µ
∂=−
∂y
⇒
22
0
22
T
tx
3
3
x
ψ
ψα
µγ
∂
∂∂
=−
∂
∂∂
⇒
22
0
22
T
tx
4
4
x
ψ
ψψ
µγ
∂∂∂
=−
∂∂∂
(2)
¾ Sîi d©y dao ®éng ë d¹ng dao ®éng riªng bËc n theo d¹ng (theo ®Ò bµi) :
()
(,) cos .sin
n
x
xt A t n
L
π
ψ
ω
⎛⎞
=⎜
⎝⎠
⎟
víi n nguyªn ⇒
()
22
2sin cos
nn
x
A
nt
tL
ψπ
ω
ω
∂⎛⎞
=− ⎜⎟
∂⎝⎠
()
2
2
2cos sin
n
nx
Atn
x
LL
ψ
ππ
ω
∂⎛⎞ ⎛
=− ⎜⎟ ⎜
∂⎝⎠ ⎝
⎞
⎟
⎠
⇒
()
4
4
4cos sin
n
nx
Atn
x
LL
ψ
ππ
ω
∂⎛⎞ ⎛
=⎜⎟ ⎜
∂⎝⎠ ⎝
⎞
⎟
⎠
Thay vµo (1) :
4
2
0
n
L
Tn
L
π
γ
ε
π
⎛⎞
⎜⎟
⎝⎠
=⎛⎞
⎜⎟
⎝⎠
⇒
2
0
n
TL
γ
π
ε
⎛⎞
=⎜⎟
⎝⎠
(3)
Thay vµo (2) :
24
20
n
nn
T
L
L
π
π
µω γ
⎛⎞ ⎛⎞
−=− −
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⇒
22
20
1
n
nn
T
L
L
π
π
ωγ
µ
⎡⎤
⎛⎞⎛⎞
=+
⎢⎥
⎜⎟⎜⎟
⎝⎠⎝⎠
⎢⎥
⎣⎦
⇒
22
20
0
1
n
Tnn
TL L
γ
ππ
ωµ
⎡⎤
⎛⎞⎛⎞
=+
⎢⎥
⎜⎟⎜⎟
⎝⎠⎝⎠
⎢⎥
⎣⎦
(4)
Tõ (3) vµ (4) suy ra :
[]
2
201
n
Tn
L
π
ωε
µ
⎛⎞
=+
⎜⎟
⎝⎠
. Víi 0
T
c
µ
=⇒
[]
2
22 1
n
n
cL
π
ω
ε
⎛⎞
=
+
⎜⎟
⎝⎠
C©u 3 : Khi kh«ng kÓ ®Õn ®é cøng cña d©y :
2
22
0n
n
c
L
π
ω
⎛⎞
=⎜⎟
⎝⎠
⇒ §é hiÖu chØnh t−¬ng ®èi cña tÇn sè g¾n víi d¹ng dao ®éng riªng n, xuÊt hiÖn do kÓ ®Õn
¶nh h−ëng cña ®é cøng cña d©y: 0
00
1111
22
nnn
nn
ωωω
ε
ε
ε
ωω
∆−
=
=+−≈+−= (gi¶ thiÕt ε << 1)
⇒
2
00
22
n
n
n
TL
ω
ε
γπ
ω
∆⎛⎞
== ⎜⎟
⎝⎠
Víi n = 1 : 4
0
5,1.10
n
n
ω
ω
−
∆=; Víi n = 2 : 3
0
2,0.10
n
n
ω
ω
−
∆=; Víi n = 10 : 2
0
5,1.10
n
n
ω
ω
−
∆=
69
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Ghi chó : §é chªnh lÖch t−¬ng ®èi
0
n
n
ω
ω
∆ cµng lín, khi tÇn sè gãc cña dao ®éng riªng cµng
lín (n t¨ng). §iÒu nµy lµ dÜ nhiªn, bëi v× øng víi mét d¹ng dao ®éng riªng cã tÇn sè cao, biªn
®é sin
x
n
L
π
⎛⎞
⎜
⎝⎠
⎟
thay ®æi rÊt nhanh, h×nh d¹ng cña sîi d©y bÞ thay ®æi m¹nh h¬n vµ ¶nh h−ëng
cña ®é cøng cña d©y lín lªn râ rÖt.
70