Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
BµI tËp Ch−¬ng III : Sãng ©m trong chÊt láng
@ ¸p dông 3: C©n b»ng n¨ng l−îng côc bé ®èi víi mét sãng ph¼ng (Trang 107)
H·y viÕt biÓu thøc cña mËt ®é ®éng n¨ng, mËt ®é thÕ n¨ng vµ mËt ®é n¨ng l−îng sãng, còng
nh− vect¬ mËt ®é dßng n¨ng l−îng (vect¬ mËt ®é n¨ng th«ng
Π
G
), ®èi víi mét sãng ph¼ng lan
truyÒn theo ph−¬ng song song víi trôc Ox. KiÓm nghiÖm biÓu thøc c©n b»ng n¨ng l−îng côc bé
trong tr−êng hîp ®Æc biÖt nµy.
Bµi gi¶i :
§èi víi mét sãng ph¼ng lan truyÒn theo ph−¬ng song song víi trôc Ox, vËn tèc v vµ ¸p suÊt d−
p cã d¹ng :
0
v( , )
(,)
x
SS
Sx
SS
xx
xt f t g t e
cc
xx
p
xt c f t g t e
cc
ρ
⎧⎡⎤
⎛⎞⎛⎞
=−++
⎪⎢⎥
⎜⎟⎜⎟
⎝⎠⎝⎠
⎪⎣⎦
⎨⎡⎤
⎛⎞⎛⎞
⎪=−−+
⎢⎥
⎜⎟⎜⎟
⎪⎝⎠⎝⎠
⎣⎦
⎩
GG
G
MËt ®é khèi cña ®éng n¨ng : 22
00
11
v(
22
K
ef
)
ρρ
==+g
⇒ 22
0
1(2 )
2
K
effgg
ρ
=++
MËt ®é khèi cña thÕ n¨ng :
() ()
22
222
00
11 1
() (2
22 2
P S SS SS
ep cfg cffg
χχρ χρ
== −= −+
2
)
g
Mµ : 2
0
1
S
S
c
ρ
χ
= ⇒ 22
0
1(2
2
P
effg
ρ
=−+
)
g
MËt ®é khèi cña n¨ng l−îng sãng ©m : 22
0()
SKP
eee f g
ρ
=+= +
Vect¬ mËt ®é n¨ng th«ng : 0
v()(
Sx
pcfgfg
ρ
Π= = − +
G)e
G
G⇒ 22
0()
Sx
cf ge
ρ
Π= −
G
G
BiÓu thøc c©n b»ng n¨ng l−îng côc bé : 0
S
e
div t
Π
+=
∂
. Tr−êng hîp sãng ©m lan truyÒn
theo ph−¬ng Ox (mét chiÒu), ta cã: 0
S
e
x
t
∂
∂Π
+
=
∂∂
DÔ dµng kiÓm tra l¹i biÓu thøc c©n b»ng n¨ng l−îng côc bé :
Ta cã : 00
11
(2 2 ) 2 2 ( )
SS
SS
fg
cf gc fg f
xxx cc
ρρ
⎡⎤
∂Π ∂ ∂
=−=−−=−
⎢⎥
∂∂∂ ⎣⎦
0
g
ρ
+
(1)
Vµ : 0
2(' ')2( )
S
e
0
f
fgg fg
t
ρρ
∂=+=
∂+
(2)
Tõ (1) vµ (2) suy ra : 0
S
e
x
t
∂
∂
Π+=
∂∂
@ ¸p dông 4 : Ph¶n x¹ vµ truyÒn qua c¸c sãng ©m trªn bÒ mÆt tiÕp gi¸p gi÷a hai èng
dÉn: (Trang 112)
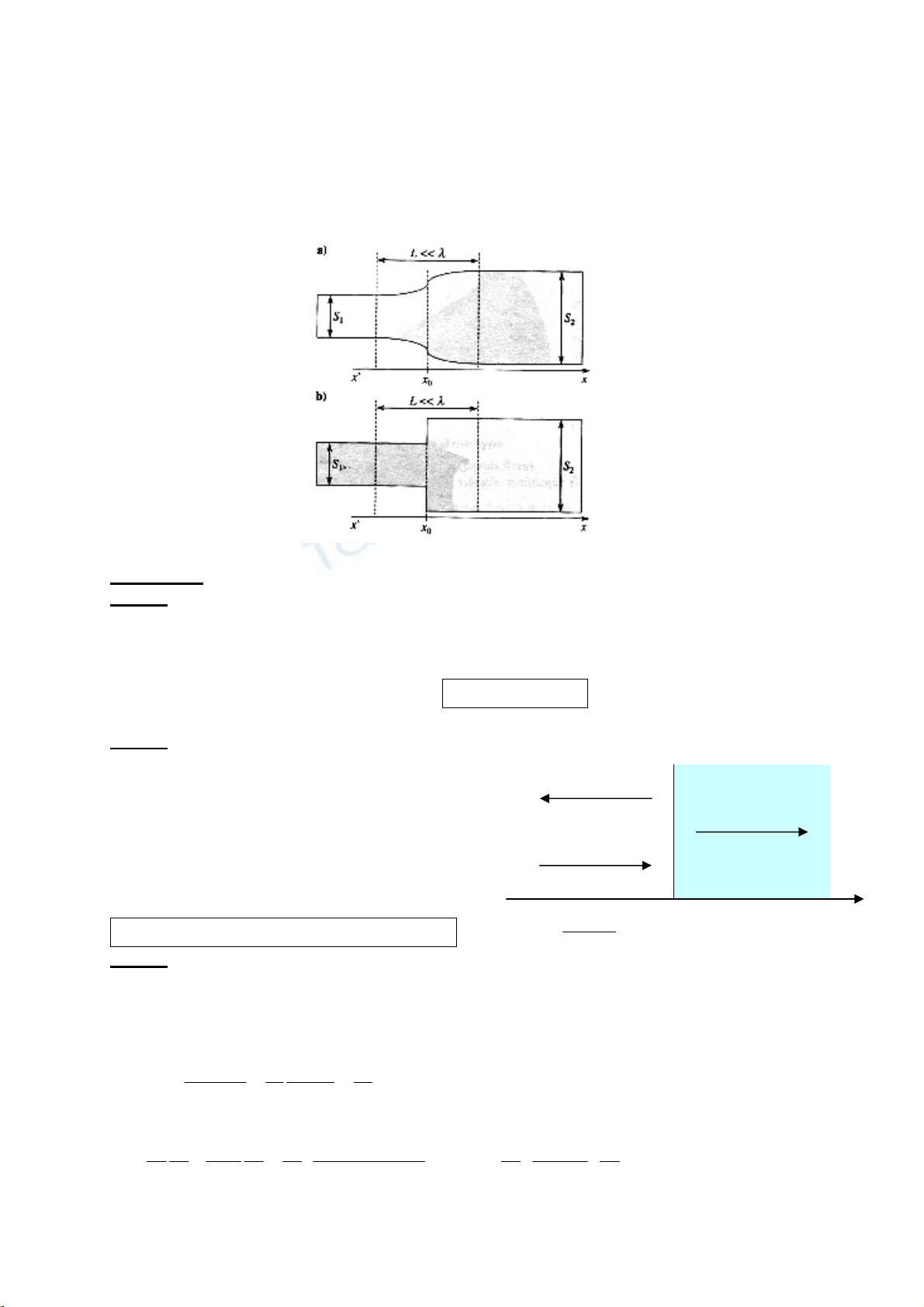
Kh¶o s¸t sù ph¶n x¹ vµ sù truyÒn qua cña c¸c sãng ©m ph¼ng trªn bÒ mÆt tiÕp gi¸p cña hai èng
dÉn cã tiÕt diÖn S1 vµ S2 (h×nh a vµ h×nh b).
1) Chøng minh r»ng cã sù liªn tôc cña ¸p suÊt t¹i x = x0 :
10 20
(,) (,)
p
xt pxt=
2) Chøng minh r»ng cã sù liªn tôc cña l−u l−îng khèi (l−u l−îng thÓ tÝch) trªn bÒ mÆt tiÕp gi¸p:
v1 0 1 1 0 v2 0 2 2 0
( ,) v( ,) ( ,) v( ,)D xt S xt D xt S xt===
Cho biÕt trë kh¸ng ©m cña mét èng dÉn cã tiÕt diÖn S ®−îc x¸c ®Þnh bëi tû sè : 0S
c
ZS
ρ
=
71
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
3) ViÕt biÓu thøc cña c¸c hÖ sè ph¶n x¹ vµ hÖ sè truyÒn qua vÒ biªn ®é ®èi víi l−u l−îng khèi
vµ ¸p suÊt d− theo c¸c trë kh¸ng ©m cña c¸c èng dÉn.
4) Tõ ®ã rót ra hÖ sè ph¶n x¹ R vµ hÖ sè truyÒn qua T vÒ n¨ng l−îng.
5) §¬n gi¶n c¸c biÓu thøc thu ®−îc khi c¸c èng dÉn chøa cïng mét chÊt l−u vµ cã diÖn tÝch
kh¸c nhau. X¸c ®Þnh T vµ R khi S2 → ∞. B×nh luËn kÕt qu¶ nhËn ®−îc.
@ Bµi gi¶i :
C©u 1 :
XÐt mét “pÝtt«ng” (mét líp chÊt l−u) cã khèi l−îng M, bÒ dµy kh«ng ®¸ng kÓ, n»m trªn bÒ mÆt
tiÕp gi¸p cña hai èng dÉn. D−íi t¸c dông cña ¸p suÊt d− p1(x0,t) vµ p2(x0,t), ph−¬ng tr×nh chuyÓn
®éng cña pÝtt«ng cã d¹ng : 10 20
() [ ( ,) - ( ,)]
M
at Sp x t p x t= trong ®ã a(t) lµ gia tèc cña pÝtt«ng.
Khi M → 0, do gia tèc a(t) lµ h÷u h¹n, nªn : 10 20
(,) = (,)
p
xt pxt
Nh− vËy, cã sù liªn tôc cña ¸p suÊt t¹i x = x0 (trªn bÒ mÆt tiÕp gi¸p gi÷a hai èng).
C©u 2 :
H×nh 5:
(
)
11
1( , )c
ρ
Sãng tíi
Sãng ph¶n x¹
Sãng truyÒn qua
()
22
2( , )c
ρ
x
0
x
x’
ChiÒu dµi L cña rèi lo¹n nhá cña chÊt l−u khi cã
sãng ©m truyÒn qua lµ bÐ h¬n nhiÒu so víi b−íc
sãng λ cña sãng ©m : L << λ, do ®ã cã thÓ bá qua
sù biÕn thiªn cña thÓ tÝch cña mét líp chÊt l−u
®ang chuyÓn ®éng do nh÷ng rèi lo¹n nhá nãi trªn
g©y ra.
Khi ®ã, ta thÊy l−u l−îng khèi trªn bÒ mÆt tiÕp
gi¸p cña hai èng dÉn lµ liªn tôc:
v1 0 1 1 0 v2 0 2 2 0
( ,) v( ,) ( ,) v( ,)D xt S xt D xt S xt===
C©u 3 :
§iÒu kiÖn biªn : 10 20
v1 0 v2 0
(,) = (,)
(,) (,)
p
xt pxt
Dxt Dxt
⎧
⎨=
⎩ ⇒
[
]
[]
1110 10 2220
110 10 220
(,) (,) = (,)(1)
(,) (,) = (,) (2)
cfxt gxt cfxt
Sfxt gxt Sfxt
ρρ
⎧−
⎪
⎨+
⎪
⎩
HÖ sè ph¶n x¹ vÒ biªn ®é ®èi víi l−u l−îng khèi :
,11
12
,1
v
() v
V phanxa phanxa
V
Vtoi toi
DSg
rD DS
== =
1
f
Tõ (1) vµ (2), suy ra :
22 222 2 211 122
1
111 111
222
Sf cf f S c S c
fSc Sc
ρρ
ρρ
⎡⎤
+
=+ =
⎢⎥
⎣⎦
ρ
⇒ 21 22
1
11
2
f
ZZS
f
Z
S
⎛⎞
+
=⎜⎟
⎝⎠
(3)
72
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Vµ : 2112122
1
11 1
-
2
f
cS S c
gcS
ρρ
ρ
⎡⎤
=⎢⎥
⎣⎦
⇒ 21 22
1
11
2
f
ZZS
g
Z
S
⎛⎞
−
=⎜⎟
⎝⎠
Suy ra : 12
12
12
()
V
Z
Z
rD
Z
Z
−
=+
T−¬ng tù, hÖ sè ph¶n x¹ vÒ biªn ®é ®èi víi ¸p suÊt d− :
11 1 1 1 2
12 12
11 1 1 1 2
() ( )
phanxa
V
toi
pcg g Z Z
rp rD
pcffZZ
ρ
ρ
−−
= = =− =− =−
+
(L−u ý dÊu (-) trong biÓu thøc cña ¸p suÊt d− ph¶n x¹).
HÖ sè truyÒn qua vÒ l−u l−îng khèi :
,22
12
,1 1
v
() v
V truyenqua truyenqua
V
Vtoi toi
DSS
DDS S
τ
== =
2
1
f
f
Tõ (3) suy ra : 21
112
21
2
f
ZS
f
ZZS
=+ ⇒ 1
12
12
2
()
V
Z
D
Z
Z
τ
=
+
T−¬ng tù, hÖ sè truyÒn qua vÒ biªn ®é ®èi víi ¸p suÊt d− :
222 22 1 1 1 1 1
12 12
111 11 1 2 2 2 1 2 2
22
() ( )
V
cf c Z S Z Z Z
pD
cf cZ ZS ZZ Z Z
ρ
ρ
ττ
ρρ
== = =
++
o HÖ sè ph¶n x¹ vµ hÖ sè truyÒn qua vÒ n¨ng l−îng :
1
1
phanxa x
toi x
Se
RSe
Π
=Π
GG
GG vµ 2
1
phanxa x
toi x
Se
TSe
Π
=Π
GG
GG
Víi :
2
111
.v
toi toi toi
pc
ρ
Π= = f
2
11 1
.v
phanxa phanxa phanxa
p
cg
ρ
Π= =−
2
22 2
.v
truyenqua truyenqua truyenqua
p
cf
ρ
Π= =
Suy ra :
2
11 1
2
11 1
cg
Rcf
ρ
ρ
= ⇒
2
12
12
ZZ
RZZ
⎛⎞
−
=⎜⎟
+
⎝⎠
()()
2
222
22 2 1 22 2 1 1 2 1
22
2
11 1 1 11 1 2 1
12 12
44cS g cS S Z Z Z
TcS f cS S Z
ZZ ZZ
ρρ
ρρ
⎛⎞
== =
⎜⎟ ++
⎝⎠
()
⇒ 12
2
12
4ZZ
ZZ
=+
T
Ta thÊy : R + T = 1
C©u 5 :
Khi èng dÉn chøa cïng mét chÊt l−u th× : ρ1 = ρ2
Ta cã : 2111
1222
/
/
2
1
Z
cS S
Z
cS S
ρ
ρ
==
⇒ 21
12 12
21
() (
V
SS
rD rp
SS
−
==−
+)
12
12 12
12 1
2
() (
V
SS
Dp
SS S
ττ
==
+)
2
21
21
SS
RSS
⎛⎞
−
=⎜⎟
+
⎝⎠
()
212
21
4SS
TSS
=+
Khi S2 → ∞ th× R → 1, T → 0. N¨ng l−îng sãng ©m bÞ ph¶n x¹ hoµn toµn vµ gÇn nh−
kh«ng truyÒn ®−îc qua bÒ mÆt tiÕp gi¸p gi÷a hai èng.
73
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Khi S2 >> S1 th×
()
212
21
41
SS
TSS
=<
+<
(v× 1
≈
) ⇒ Khi ®ã, n¨ng l−îng sãng ©m truyÒn qua bÒ
mÆt tiÕp gi¸p rÊt bÐ. V× vËy, khi nãi tr−íc ®¸m ®«ng, ta ph¶i dïng tay lµm loa hoÆc dïng loa th×
n¨ng l−îng sãng ©m truyÒn tõ miÖng truyÒn ra bªn ngoµi míi lín ®−îc.
@ Bµi tËp 1: Giã mang ©m thanh (Trang 129)
Nghiªn cøu mét dßng kh«ng khÝ cã vËn tèc kh«ng ®æi u0 (theo ph−¬ng chiÒu trôc Ox víi u0 > 0
t¹i mäi ®iÓm. Trong dßng ch¶y ®ã, cã mét sãng ©m ph¼ng ch¹y truyÒn theo ph−¬ng cña trôc
Ox.
1) H·y dïng c¸c ký hiÖu ®· häc, h·y viÕt ph−¬ng tr×nh lan truyÒn ¸p suÊt d− p(x,t) trong ph¹m
vi phÐp gÇn ®óng ©m häc.
2) Mét sãng ph¼ng ch¹y ®¬n s¾c, lan truyÒn trong dßng ch¶y. D−íi d¹ng phøc, p ®−îc viÕt nh−
sau: (
0itkx
ppe
ω
−
=)
. H·y t×m hÖ thøc t¸n x¹ cho mèi liªn hÖ gi÷a k vµ ω, vµ gi¶i thÝch kÕt qu¶
nhËn ®−îc. C©u “giã mang ©m thanh” nãi lªn ®iÒu g×?
Bµi gi¶i : C©u 1 :
VËn tèc cña mét phÇn tö chÊt l−u khi giã chuyÓn ®éng víi vËn tèc u0 :
víi
0v( , )ux+t0
v( , )
x
tu<<
Tõ ph−¬ng tr×nh b¶o toµn khèi l−îng :
()
0
(v)div u
t0
ρ
ρ
+
+=
G
G, suy ra :
()()
00
vvdiv u u grad
t0
ρ
ρρ
∂++++
∂
JJJJJG
GG GG =
L−u ý r»ng : ρ = ρ0 + µ víi ρ0 = h»ng sè; 0
u
G
b»ng h»ng sè, ta cã :
()
0
vvdiv u grad
t0
µ
ρµ
∂+++ =
∂
JJJJJG
GGG
Do 0
ρ
ρµ
=+ nªn :
() ()
00
vv vdiv div u grad grad
t0
µ
ρµ µµ
∂++++
∂=
J
JJJJG JJJJJG
GGG G
MÆt kh¸c, do 0
µ
ρ
<< vµ 0
vu<< nªn :
0
v<< vdiv div
µ
ρ
GG
vµ
0
v0grad u grad
µµ
<< =
JJJJJG JJJJJG
GG
Do ®ã : 00
v0div u grad
t
µ
ρµ
∂++
∂
JJJJJG
GG =
Tr−êng hîp truyÒn sãng mét chiÒu, ta cã : 00
v0
u
txx
µ
µ
ρ
∂
∂∂
+
+=
∂
∂∂
(1)
Ph−¬ng tr×nh Euler :
()
v
vvv
grad gradP f
t
ρ
∂
⎛⎞
+=−
⎜⎟
∂
⎝⎠
GJJJJJG JJJJJG+
G
GG trë thµnh :
()
000
(v) (v) (v)
uugradu grad
t
ρρ
∂+
⎛⎞
++ +=−
⎜⎟
∂
⎝⎠
GG JJJJJG JJJJJG
GG GG P
(Ghi chó :
Ph−¬ng tr×nh Euler
()
v
vvv
grad gradP f
t
ρ
∂
⎛⎞
+=−
⎜⎟
∂
⎝⎠
GJJJJJG JJJJJG+
G
GG víi v
G
ë ®©y b»ng
0vu+
GG
Bá qua lùc thÓ tÝch v
f
G
).
L−u ý r»ng : P = P0 + p vµ P0 = h»ng sè; 0
u
G
lµ h»ng sè, suy ra :
74
Baìi táûp Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
()
0
v(v) v
u grad grad p
t
ρρ
∂
⎛⎞
++ =−
⎜⎟
∂
⎝⎠
GJJJJJG JJJJJG
GG G
⇒ 0
v( )v+ (v )v
u grad grad grad p
t
ρρ ρ
∂+=
∂
GJJJJJG JJJJJG JJJJJG
GGGG
−
Trong phÐp gÇn ®óng ©m häc, ta cã : v
(v )v<<
grad t
∂
∂
G
J
JJJJG
G
G ; ®ång thêi l−u ý r»ng 0
vv
tt
ρρ
∂∂
≈
∂∂
GG
⇒ 000
v()v
u grad grad p
t
ρρ
∂+=−
∂
GJJJJJG JJJJJG
GG
Tr−êng hîp lan truyÒn theo mét chiÒu Ox, ta cã :
000
vvp
u
tx
ρρ
∂∂
+=−
∂∂
x
∂
∂
(2)
(Ghi chó :
vv
vv
(.grad)v
xx
xyz
yy
xyz
zz
xyz
uuu
v
v
x
y
z
x
yz
uuuu
x
yz
A
AA
uuu
x
yz
∂∂∂
⎧++
⎪∂∂∂
⎪∂∂∂
⎪
=++
⎨∂∂
⎪
⎪∂∂∂
++
⎪∂∂∂
⎩
JJJJG
GG
∂
)v
, do ®ã nÕu lan truyÒn theo mét chiÒu th×
trë thµnh
0
(ugrad
JJJJJG
GG
0
v
u
x
∂
∂)
Víi gi¶ thiÕt N§H: 02
1
Sp
c
µρχ
==p
trong ®ã : 0
2
1
S
c
ρ
χ
=, biÓu thøc (1) trë thµnh:
0
0
22
1v0
u
pp
ct xcx
ρ
∂∂∂
++=
∂∂∂
(3)
⇒
222
0
0
22 2
1v0
u
pp
ct xtcxt
ρ
∂∂∂
++
∂∂∂∂∂
=
(4)
Tõ biÓu thøc (2) suy ra :
22
000
2
vv
2
2
p
u
x
tx
ρρ
∂∂
+=−
∂∂ ∂ ∂
x
∂
(5)
Tõ biÓu thøc (3) suy ra :
222
0
0
222
1v
0
u
pp
cxt x cx
ρ
∂∂∂
++
∂∂ ∂ ∂2
=
(6)
Tõ (6) rót ra :
22
0
022 2
v1 u2
2
p
p
x
cxtcx
ρ
∂∂
=− −
∂∂∂
∂
∂
Tõ (4) rót ra :
22
0
022 2
v1 u2
p
p
x
tctcx
ρ
∂∂
=− −
∂∂ ∂ ∂∂
t
∂
Thay tÊt c¶ vµo (5), suy ra :
75