
TRẦN ĐỨC NGỌC - YÊN SƠN, ĐÔ LƢƠNG, NGHỆ AN - GV THPT TÂN KỲ I – ĐT : 0985128747
1
************************************************************
MỘT SỐ BÀI TOÁN GIẢI PT, HỆ PT MŨ VÀ LOGARIT
Bài số 1 :
a/ Giải hệ phương trình
Lời giải : Điều kiện
Hệ phƣơng trình tƣơng đƣơng với hệ :
Đặt: Ta có ( I )
Nhân hai phƣơng trình của hệ ( I ) vế theo vế , đƣợc: 3(3x+2y)(3x-2y) = (*)
Kết hợp (1) với (*) Ta có 15 = Do đó t = 1Thế vào hệ ( I ) đƣợc hpt :
Thỏa mãn điều kiện đã nêu .
Nên đây là nghiệm của hệ phƣơng trình
Lời giải 2: Điều kiện
Hệ phƣơng trình tƣơng đƣơng với hệ :
Nhân hai vế phƣơng trình (2) với và áp dụng = (Với mọi a,b,c
dƣơng a và b ) Ta đƣợc :
( Vì từ pt (1) suy ra 3x-2y = )
3x+2y = 5 (2’)
Kết hợp với phƣơng trình (1) Ta đƣợc hệ phƣơng trình : Thỏa
mãn điều kiện đã nêu Nên đây là nghiệm của hệ phƣơng trình đã cho
b/ Giải hệ phương trình :
Lời giải : Điều kiện
Hệ phƣơng trình tƣơng đƣơng với :

TRẦN ĐỨC NGỌC - YÊN SƠN, ĐÔ LƢƠNG, NGHỆ AN - GV THPT TÂN KỲ I – ĐT : 0985128747
2
Thỏa mãn điều kiện
Nên là nghiệm của hệ phƣơng trình đã cho.
Bài số 2 :
Giải hệ phương trình
Lời giải : Điều kiện xy .
= Suy ra: =
Phƣơng trình (1) trở thành : - - 2 = 0 Đặt t = Ta có t2 – t – 2 =
0 t = 2 ( Loại t = - 1 )
Nhƣ vậy: = 2 Do đó = 1 (1’) .
Hệ phƣơng trình đã cho tƣơng đƣơng với hệ phƣơng trình
-Hệ (II) có hai nghiệm : và Cả hai nghiệm này đều thỏa mãn
điều kiện xy Nên đây là hai nghiệm của hệ phƣơng trình đã cho.
Bài số 3 :
Tìm giá trị của tham số m để phương trình sau đây có 3 nghiệm phân biệt :
- - 2mx + m2 = 2 – x2
Lời giải : Viết phƣơng trình thành :
4. = 2. - (x – m)2 =
2. = (x – m)2 (*) (Chú ý : = )
Bài toán trở thành :Tìm giá trị của m để phƣơng trình (*) có 3 nghiệm phân biệt.
-Viết phƣơng trình (*) thành :
2. =

TRẦN ĐỨC NGỌC - YÊN SƠN, ĐÔ LƢƠNG, NGHỆ AN - GV THPT TÂN KỲ I – ĐT : 0985128747
3
(Đặt t = x – 1)
Nhận thấy : Phƣơng trình ( 1 ) và phƣơng trình ( 1’) đều không thể có hai nghiệm trái dấu (Do
các hệ số a , c cùng dấu ) Để phƣơng trình (*) có 3 nghiệm phân biệt thì :
Không thể xẩy ra các trường hợp :
*- Trong hai pt (1) và (1’) : một phương trình có hai nghiệm cùng dấu – cả 2 nghiệm thỏa mãn
điều kiện ; Phương trình kia có hai nghiệm trái dấu – một nghiệm thỏa mãn điều kiện và một
nghiệm bị loại
**- Hai phương trình (1) và (1’) đều có hai nghiệm phân biệt , đồng thời chúng có một nghiệm
chung
Do vậy mà phƣơng trình (*) có 3 nghiệm phân biệt chỉ khi một trong 2 trƣờng hợp sau xẩy ra:
-Trường hợp 1: pt (1) có hai nghiệm dƣơng phân biệt ,đồng thời pt ( 1’) có
nghiệm kép t0
Điều này xẩy ra m =
-Trường hợp 2: pt (1) có nghiệm kép dƣơng , đồng thời phƣơng trình (1’) có 2
nghiệm âm phân biệt
Điều này xẩy ra m =
Trả lời :Có hai giá trị của m để phƣơng trình đã cho có 3 nghiệm phân biệt là
m1 = và m2 =
(Bài kiểm tra Học Kỳ I năm học 2009-2010 Lớp 12 CB Trƣờng THPT Tân kỳ I
Tỉnh Nghệ an – Thầy Đặng Hữu Trung ra đề )
Bài số 4 : Giải và biện luận theo tham số m phƣơng trình sau :
(1)
Lời giải :Viết phƣơng trình thành dạng mới
Lời giải : (Cùng dạng với Bài số 3 ở trên).Ta có : =
x2 + 2mx + m = 0 (2)

TRẦN ĐỨC NGỌC - YÊN SƠN, ĐÔ LƢƠNG, NGHỆ AN - GV THPT TÂN KỲ I – ĐT : 0985128747
4
-Giải và biện luận phƣơng trình (1) Đƣa về giải và biện luận phƣơng trình (2).
*Nếu ’= m2-m < 0 Tức là 0 < m < 1 Thì phƣơng trình vô nghiệm
*Nếu ’= m2- m = 0 Tức là m1 = 1 m2 = 0 Thì phƣơng trình có nghiệm
Kép (m = 1nghiệm kép x = - 1 ; m = 0 nghiệm kép là x = 0 )
*Nếu ’= m2- m > 0 Tức là : m < 0 hoặc m > 1 thì phƣơng trình có hai
nghiệm phân biệt x1 = - m - và x1 = - m + ./.
Bài số 5 :
Giải phương trình : -
Lời giải : Điều kiện x
= Ta có =
và = = .
Do đó Phƣơng trình trở thành : = ( x2 – 1 ).Chia 2 vế cho
đƣợc phƣơng trình: = x2 – 1 (*)
Điều kiện x2 – 1 , kết hợp điều kiện x .Ta suy ra điều kiện x .
Với điều kiện x Lấy lôgarit cơ số 3 hai vế phƣơng trình (*),đƣợc phƣơng trình
tƣơng đƣơng : = = t (Đặt = t ) Thì có hpt:
x = 2 thỏa mãn điều kiện x .
Trả lời : Phƣơng trình có nghiệm x = 2
Bài số 6 :
Giải phương trình :
Lời giải : Lấy lôgarit cơ số 2 hai vế ,đƣợc = (x – 2)
(x – 2) = 0
Bài số 7 : Giải phương trình : 2.
Lời giải : Điều kiện
Đặt t = 2. Thì : (*) :
Thế (2) vào (1) suy ra Chia
hai vế phƣơng trình cho đƣợc :
Phƣơng trình này có nghiệm duy nhất t = - 1 (Nhẩm nghiệm ,Chứng minh
duy nhất – Dựa vào tính chất các hàm số liên tục ).Thế t = -1 vào hpt (*)
TRẦN ĐỨC NGỌC - YÊN SƠN, ĐÔ LƢƠNG, NGHỆ AN - GV THPT TÂN KỲ I – ĐT : 0985128747
5
Nhƣ vậy ta có : x = , k z là nghiệm của pt
Bài số 8 :
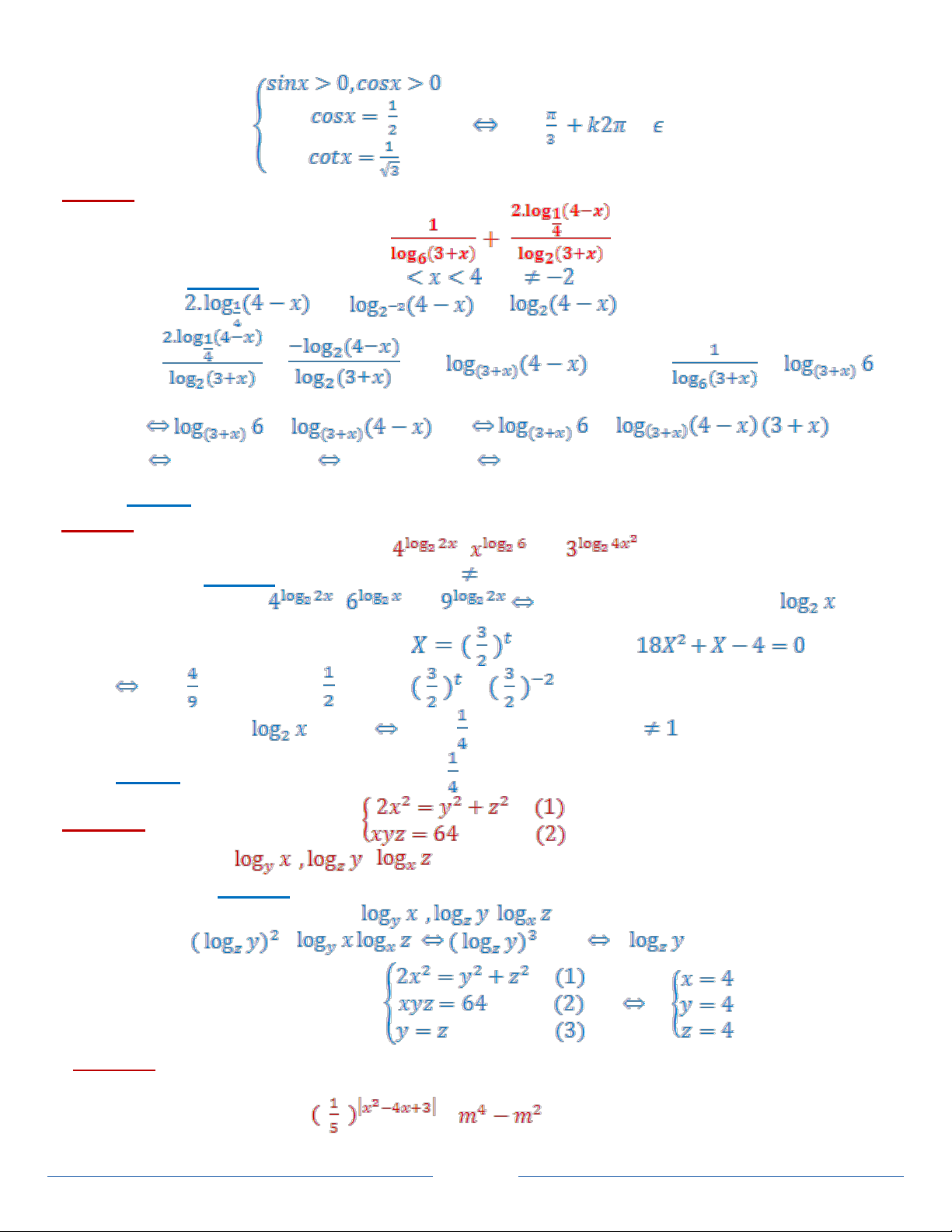
Giải phương trình : = 1 (*)
Lời giải : Điều kiện - 3 và x
Chú ý : = 2. = -
Nên = = - và lại có =
Do đó ta có :
(*) - = 1 =
6 = (4-x)(3+x) x2-7x -18 = 0 x = 9 ( Loại x = -2 )
Trả lời : Phƣơng trình có nghiệm x = 9 .
Bài số 9 :
Giải phƣơng trình : - = 2.
Lời giải : Điều kiện x > 0 , x 1 Phƣơng trình viết thành :
- = 2. 4.4t – 6t - 18.9t = 0 .với t = .Chia
hai vế phƣơng trình cho 4t rồi đặt > 0 đƣợc pt :
X = ( Loại X = - ) Vậy = , t = -2
Nhƣ vậy ta có: = - 2 x = (Thỏa mãn 0 < x ).
Trả lời : Phƣơng trình có nghiệm x =
Bài số 10 : Giaỉ hệ phƣơng trình
với điều kiện ,theo thứ tự đó lập thành cấp số nhân (3)
Lời giải : Điều kiện x , y , z đều dƣơng và khác 1
Theo giả thiết theo thứ tự đó lập thành cấp số nhân
suy ra: = = 1 = 1 suy ra y = z
Do đó ,ta có hệ phƣơng trình : là nghiệm hpt
Bài số 11 :
Với giá trị nào của tham số m thì phƣơng trình sau đây có 4 nghiệm phân biệt :
= + 1 (*)

























![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




