Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 117
CHÆÅNG 8
BIÃÚN ÂÄØI TÆÅNG ÂÆÅNG MAÛCH TUYÃÚN TÊNH
Pheïp biãún âäøi tæång âæång :
Ta âaî biãút viãûc xeït, tênh toaïn maûch âiãûn laì láûp vaì giaíi hãû phæång trçnh Kirhof 1, 2
maì säú phæång trçnh naìy tuìy thuäüc vaìo säú nuït, nhaïnh cuía maûch âiãûn. Säú phæång trçnh
caìng êt thç viãûc giaíi caìng nhanh, goün, âån giaín.
Vç säú phæång trçnh tuìy thuäüc säú nuït, nhaïnh cuía så âäö maûch nãn ta âàût váún âãö tçm
caïch dáùn ra mäüt så âäö khaïc êt nhaïnh, êt nuït hån nhæng tæång âæång våïi så âäö âaî coï,
nãn coï thãø giaíi maûch âiãûn tæång âæång âoï räöi suy ra âaïp æïng åí maûch âiãûn âaî coï. Viãûc
laìm nhæ váûy goüi laì biãún âäøi tæång âæång maûch âiãûn. Chè coï thãø dáùn ra âæåüc så âäö
tæång âæång khi viãûc biãún âäøi thoía maîn âiãöu kiãûn nháút âënh goüi laì âiãöu kiãûn biãún âäøi
tæång âæång. Thæåìng giæî nguyãn khäng âuûng chaûm mäüt säú nhaïnh hoàûc nuït cáön xeït
doìng, aïp, chè tçm caïch biãún âäøi nhæîng nhaïnh, nuït khaïc sao cho viãûc xeït doìng, aïp åí
nhaïnh xeït âæåüc tiãûn, goün nháút. Tæì âoï tháúy roî âiãöu kiãûn biãún âäøi tæång âæång laì : "
Nhæîng traûng thaïi doìng, aïp trãn nhæîng nhaïnh, nuït khäng bë biãún âäøi phaíi giæî nguyãn
giaï trë väún coï cuía noï".
Thoía maîn âiãöu kiãûn trãn thç :
Cäng suáút âæa vaìo mäùi bäü pháûn cuîng nhæ âæa vaìo táút caí nhæîng bäü pháûn khäng bë
biãún âäøi, giæî nguyãn giaï trë väún coï.
Do toaìn maûch thoía maîn âiãöu kiãûn 0Pk
=
∑
, nãn cäng suáút täøng âæa vaìo nhæîng bäü
pháûn bë biãún âäøi cuîng giæî nguyãn khäng âäøi.
Pheïp biãún âäøi thoía maîn âiãöu kiãûn âoï goüi laì pheïp biãún âäøi tæång âæång.
Caïc biãún âäøi tæång âæång thæåìng gàûp :
Váûn duûng nguyãn tàõc biãún âäøi tæång âæång ta coï âæåüc caïc så âäö tæång âæång
thæåìng gàûp nhæ sau :
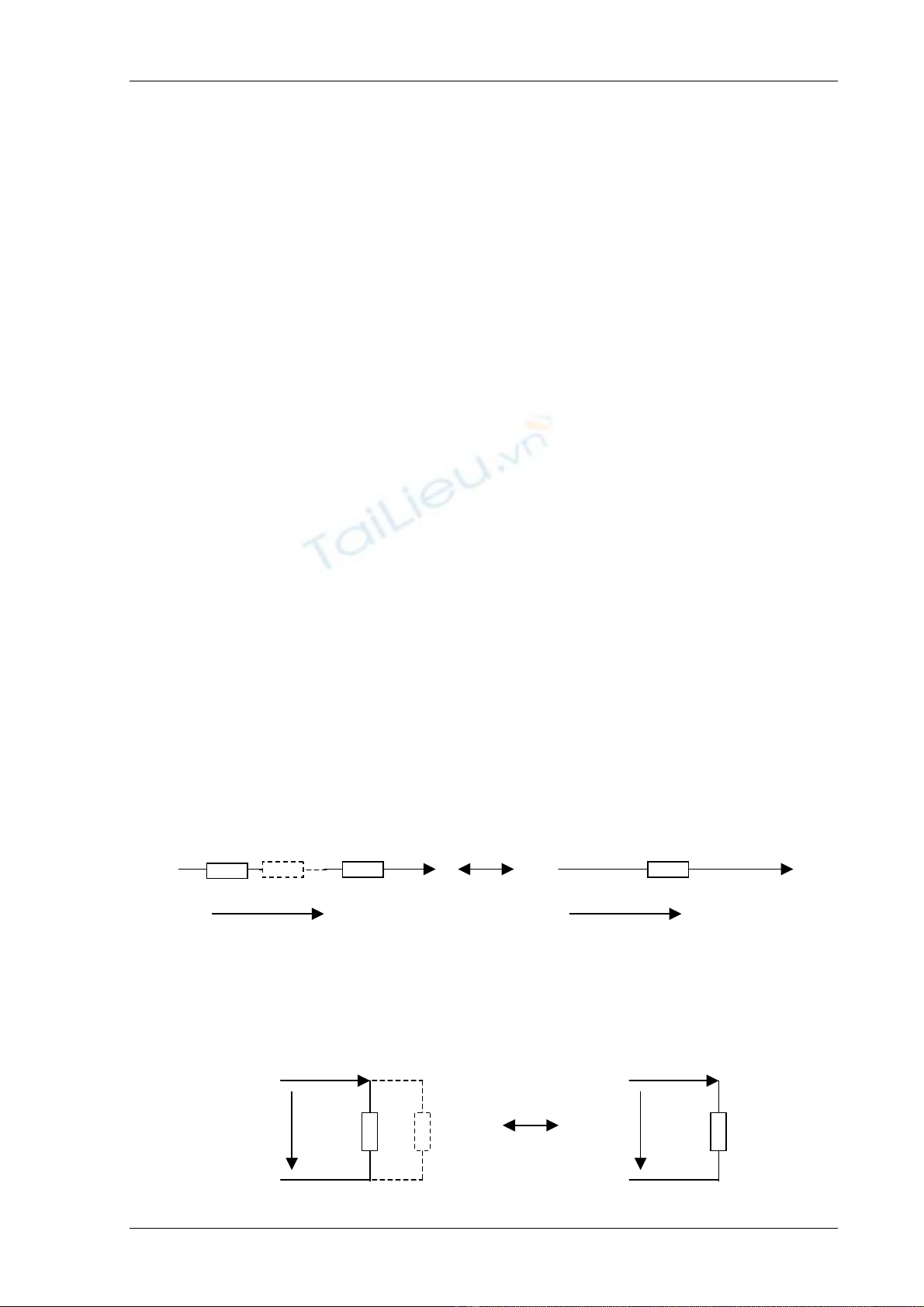
Maûch âiãûn gäöm caïc täøng tråí näúi tiãúp Zk tæång âæång våïi täøng tråí Ztâ = Z1 + Z2 + ...+
Zk = ΣZk (8-1).
U
.
I
.
U
.Ztâ
Zk
Z1
I
.
(
h.8.1
)
.
tâ
..
k21
.IZUI)Z...ZZ(U =↔+++=
Maûch âiãûn gäöm caïc nhaïnh coï täøng dáùn näúi song song nhau tæång âæång våïi täøng
dáùn ∑(8-2).
k
Y
I
.
U
.Y1 ...
(
h.8.2
)
I
.
U
.Ytâ
Yk
Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 118
.
tâ
..
k21
.UYIU)Y...YY(I =↔+++=
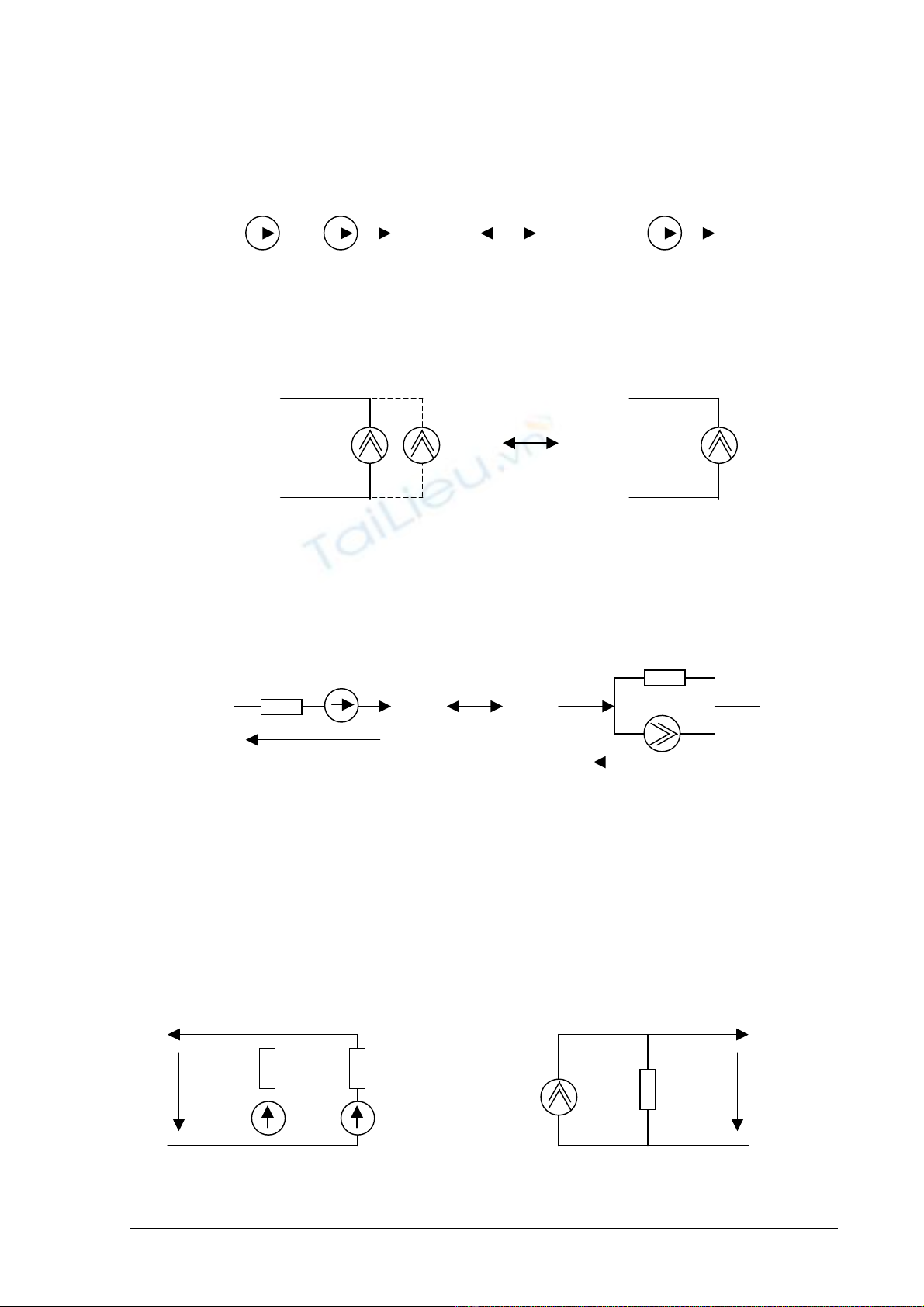
Mäüt nhaïnh gäöm caïc Sââ näúi tiãúp tæång âæång våïi 1 nhaïnh coï Sââ
(8-3).
k
.
2
.
1
.E...,,E,E
∑
=k
.
tâ
.EE
Ek
.
E1
.Etâ
.
(
h.8.3
)
Nhæîng nguäön doìng båm vaìo mäüt nuït tæång âæång våïi mäüt nguäön doìng
(8-4).
k
.
2
.
1
.J...,,J,J
∑
=k
.
tâ
.JJ
J1
.... Jk
.
(
h.8.4
)
Jtâ
.
Mäüt nhaïnh gäöm näúi tiãúp Z (nguäön Sââ - Så âäö Tãvãnin) tæång âæång mäüt så âäö
nguäön doìng näúi song song våïi Y (nguäön doìng âiãûn - Så âäö Norton) vaì ngæåüc laûi.
.
E
.
J
⎪
⎩
⎪
⎨
⎧
==
=
..
tâ
.
tâ
J.ZY/JE
Y/1Z , ⎪
⎩
⎪
⎨
⎧
==
=
Y.EZ/EJ
Z
/
1Y
..
tâ
.
tâ (8-5)
(
h.8.5
)
Z
Ytâ
Jtâ
.
U
.
I
.
I
.
E
.
U
.
Caïc nguäön aïp gäöm , Z
1
.
E1 näúi song song , Z
2
.
E2 ...våïi , Z
k
.
Ek tæång âæång våïi så
âäö nguäön doìng näúi song song täøng dáùn Y
tâ
.
Jtâ : ⎪
⎩
⎪
⎨
⎧
==
==
∑∑
∑
∑
kk
.
k
.
tâ
.
kktâ
YEJJ
Z/1YY (8-6).
I
.
(
h.8.6
)
U
. U
.
I
.
Ytâ
Zk
Z1
Jtâ
.
E1
. Ek
.
Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 119
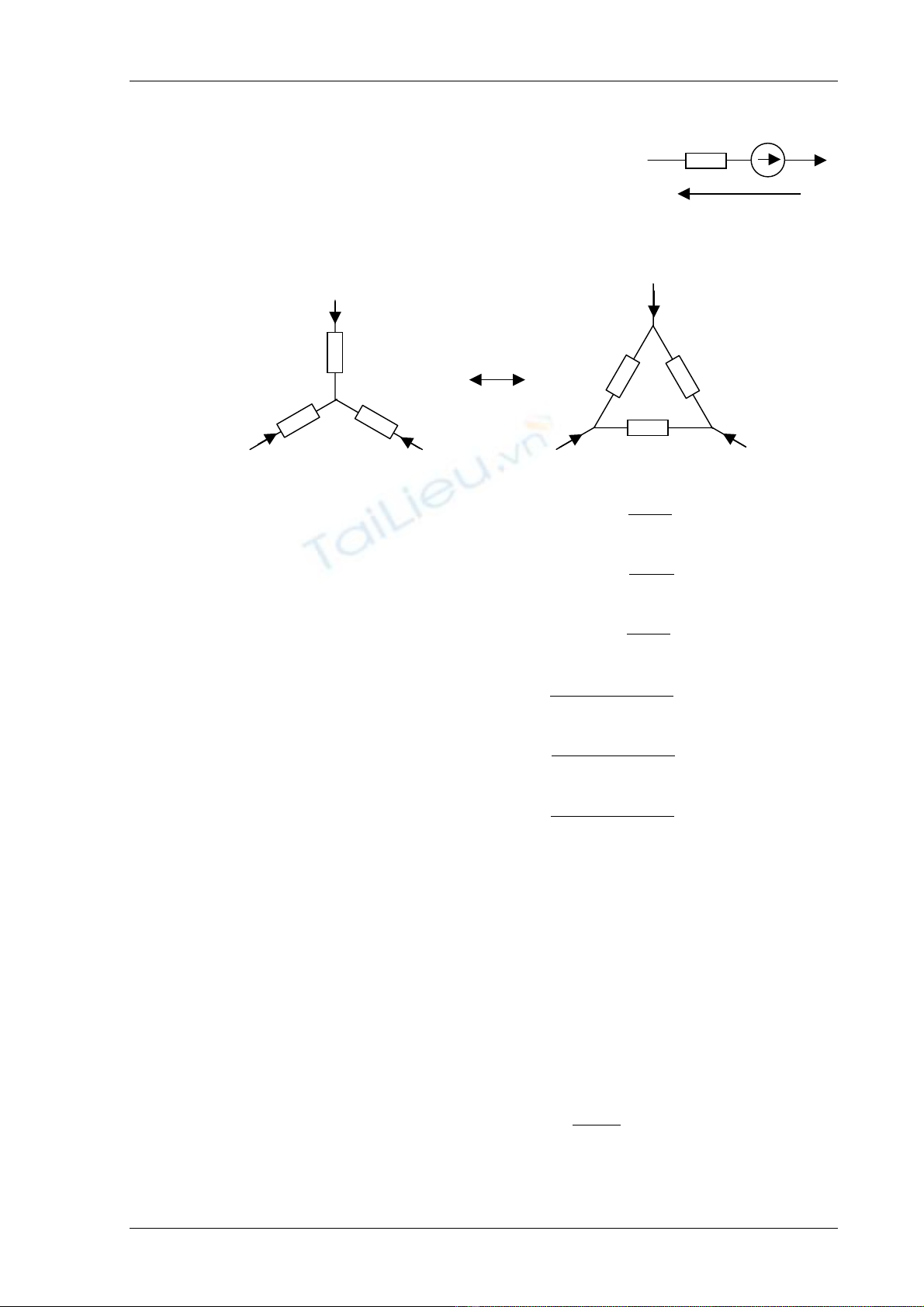
Tæì hçnh (h.8.6) tháúy coï thãø tçm mäüt så âäö tæång âæång
nguäön Sââ näúi tiãúp Z
tâ
.
E
kkktâtâ
.
tâ
.
tâtâ
Y/YY/JE
Y/1Z
tâ nhæ hçnh (h.8.7) våïi quan hãû :
(8-7).
⎪
⎩
⎪
⎨
⎧
==
=
∑∑ .
E
Ztâ Etâ
.
U
(
h.8.7
)
.
Biãún âäøi tæång âæång Y - ∆ :
3
.
I3
2
I2
.
I1
.
1
Z23
Z13
Z12
1
2 3
I1
Z3
Z2
Z1
I2
. I3
.
.
(
h.8.8
)
Biãún âäøi tæì Y sang ∆ theo cäng thæïc :
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
++=
++=
++=
2
13
1331
1
32
3223
3
21
2112
Z
ZZ
ZZZ
Z
ZZ
ZZZ
Z
ZZ
ZZZ
(8-8)
Biãún âäøi tæì ∆ sang Y theo cäng thæïc :
⎪
⎪
⎪
⎩
⎪
⎨ (8-9)
⎪
⎪
⎧
++
=
++
=
++
=
312312
1323
3
312312
2312
2
312312
1312
1
ZZZ
ZZ
Z
ZZZ
ZZ
Z
ZZZ
ZZ
Z
Thay tæång âæång mäüt så âäö hçnh sao khäng nguäön n caïnh bàòng mäüt så âäö âa giaïc
toaìn chènh n âènh.
Âa giaïc toaìn chènh laì mäüt graph coï n âènh vaì mäùi âènh âãöu coï nhæîng nhaïnh näúi
âuí (n-1) âènh khaïc. Suy ra âa giaïc coï n(n-1)/2 nhaïnh.
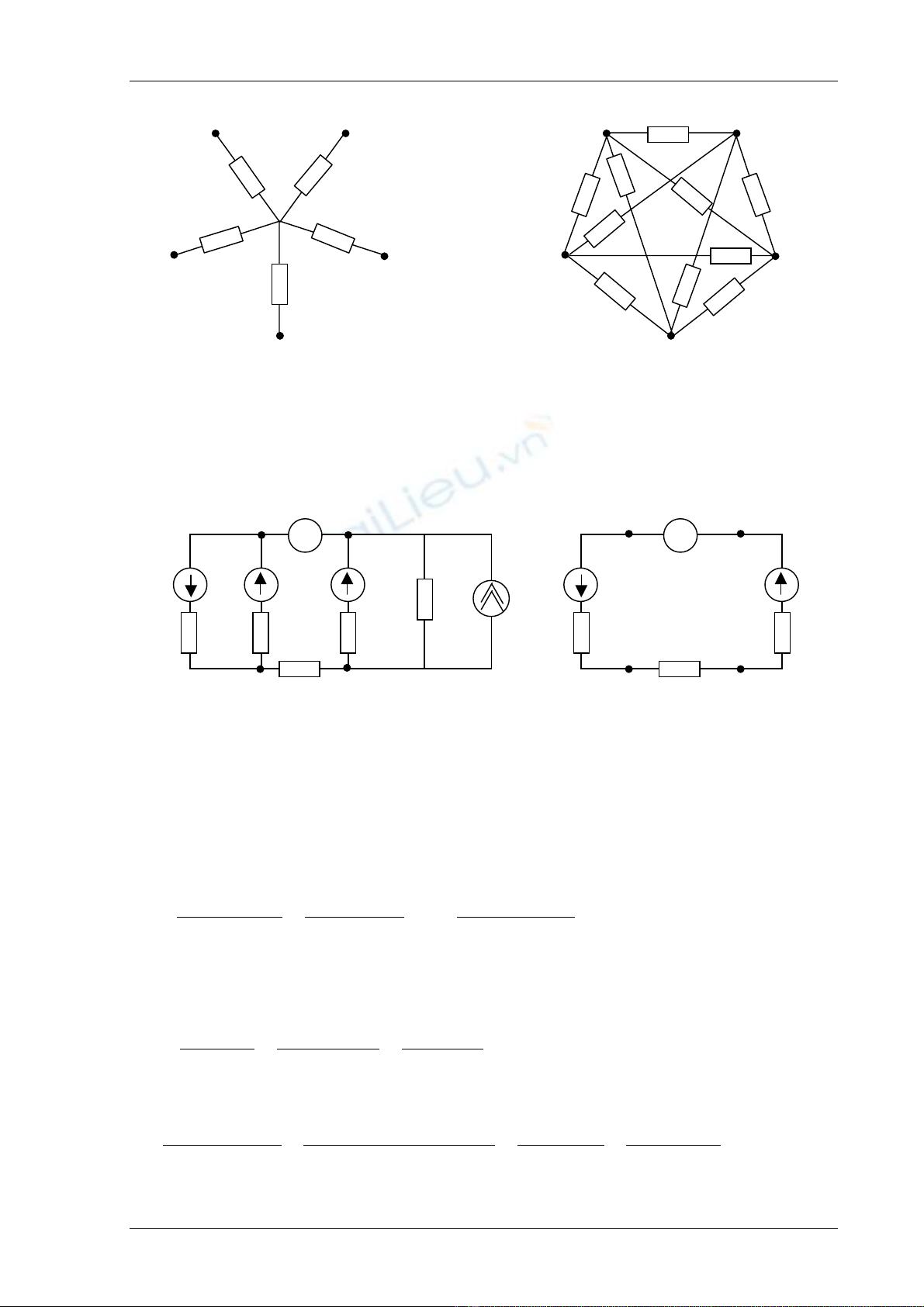
Vê duû : Så âäö hçnh sao 5 caïnh coï thãø âäøi thaình mäüt så âäö nguî giaïc toaìn chènh nhæ
hçnh (h.8.9).
Trong âoï Y1, ..., Yk laì täøng dáùn caïc nhaïnh hçnh sao, Z1, ..., Zk laì täøng tråí caïc
nhaïnh hçnh sao, Y12, ..., Y1k laì täøng dáùn caïc nhaïnh âa giaïc näúi caïc âènh ghi åí chè säú, Z12
,..., Z1k laì täøng tråí caïc nhaïnh âa giaïc tæång æïng.
Coï thãø chæïng minh ra cäng thæïc biãún âäøi : ∑
=n
1
k
lk
kl
Y
YY
Y (8-10).
Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn
Giaïo trçnh Cåí såí Kyî thuáût âiãûn I Trang 120
15
42
3
Z35
Z24
Z14
Z13
Z25
Z15
Z12
Z23 Z34
Z54
1
(a) Z3
Z2 Z4
Z5
Z1
3
2 4
5
(b)
(
h.8.9
)
Trong træåìng håüp täøng quaït baìi toaïn ngæåüc laûi : biãún âäøi hçnh âa giaïc thaình hçnh
sao n caïnh âàóng trë. Khi n > 3 laì khäng âæåüc vç säú täøng tråí (hoàûc täøng dáùn) cáön tçm cuía
caïc nhaïnh hçnh sao beï hån säú âiãöu kiãûn n(n-1)/2 maì chuïng phaíi thoía maîn. Nhæng khi
n=3 thç säú âiãöu kiãûn bàòng n(n-1)/2 = 3 do âoï luän luän coï thãø biãún âäøi Y - ∆.
Vê duû : Xaïc âënh chè säú cuía ampemeït trong maûch hçnh (h.8.10). Biãút :
A
J
.
E2
.
E1
.
Z4
Z2
Z1
a b
c d
Z5
E3
.
Z3
A
Zac
Eac
.
Z5
Ebd
.
Zbd
d
c
b
a
(
a
)
(
h.8.10
)
b
A10J,V120EEE,10jZ,20ZZ,10jZZ .
3
.
2
.
1
.
34251 ====Ω−=Ω==Ω==
Biãún âäøi caïc nhaïnh näúi song song giæîa hai nuït a, c vaì b, d âæa vãö så âäö tæång
âæång dãù daìng tênh doìng âiãûn qua ampemeït :
0
2121ac 63112,01,0j05,020
/
110j
/
1Z
/
1Z
/
1YYY 〈−=−=+=+=+= S.
nãn Ω+=〈=〈−== 8j46395,863112,0
/
1Y
/
1Z 00
acac .
)V(96j726,53120120
63112,0
6,116112,0
120
63112,0
05,01,0j
Y
YEYE
E0
0
0
0
ac
22
.
11
.
ac
.−=〈−=
〈−
〈−
=
〈−
−−
=
−
=
0
4343bd 63112,01,0j05,020
/
110j
/
1Z
/
1Z
/
1YYY 〈=+=+−=+=+=
nãn Ω−=〈−=〈== 8j46395,863112,0
/
1Y
/
1Z 00
bdbd
)V(32j13613139
63112,0
506,15
63112,0
101,0j.120
Y
JYE
E0
0
0
0
bd
.
33
.
bd
.−=〈−=
〈
〈
=
〈
+
=
+
=
Tæì så âäö hçnh (h.8.10b) tênh âæåüc doìng qua ampemeït :
)A(831,19
3,518,12
6,31244
10j8
128j208
)8j4(10j)8j4(
)32j136()96j72(
ZZZ
EE
I0
0
0
bd5ac
bd
.
ac
.
.〈−=
〈
〈−
=
+
−
=
−+++
−++
=
++
+
=
Træåìng Âaûi Hoüc Baïch Khoa - Khoa Âiãûn - Bäü män Thiãút bë âiãûn