Giáo trình Cấu trúc dữ liệu Trường THCN Công - Kỹ Nghệ Ðông Á
Trang 1
Chương V. CẤU TRÚC CÂY (TREE)
I. ĐỊNH NGHĨA VÀ MỘT SỐ KHÁI NIỆM
Cây là 1 cấu trúc phi tuyến, thiết lập trên 1 tập hữu hạn các phần tử mà ta gọi
là “nút”, trong đó có 1 nút đặt biệt được gọi là (noot), liên kết bởi 1 quan hệ phân
cấp, gọi là quan hệ cha – con.
Cây có thể được định nghĩa 1 cách đệ qui như sau :
1. Một nút là 1 cây. Nút đó cũng là gốc của cây ấy.
2. Nếu T1, T2,…,Tk là các cây với n1, n2 ,…,nk lần lượt là các gốc ; n là 1 nút
và n có quan hệ cha – con với n1, n2 ,…,nk thì lúc đó 1cây mới T sẽ được tạo lập
với n là gốc của nó. Nút được gọi là cha của n1, n2 ,…,nk ; ngược lại n1, n2 ,…,nk
được gọi là con của n. Các cây T1, T2,…,Tk được gọi là cây con (subtrees) của n.
Người ta quy ước : 1 cây không có nút nào được gọi là cây rỗng.
Trên hình vẽ, người ta biểu diễn cây với nút gốc ở trên và quan hệ cha – con
được thể hiện bởi 1 đoạn thẳng (giữa nút cha và nút con).
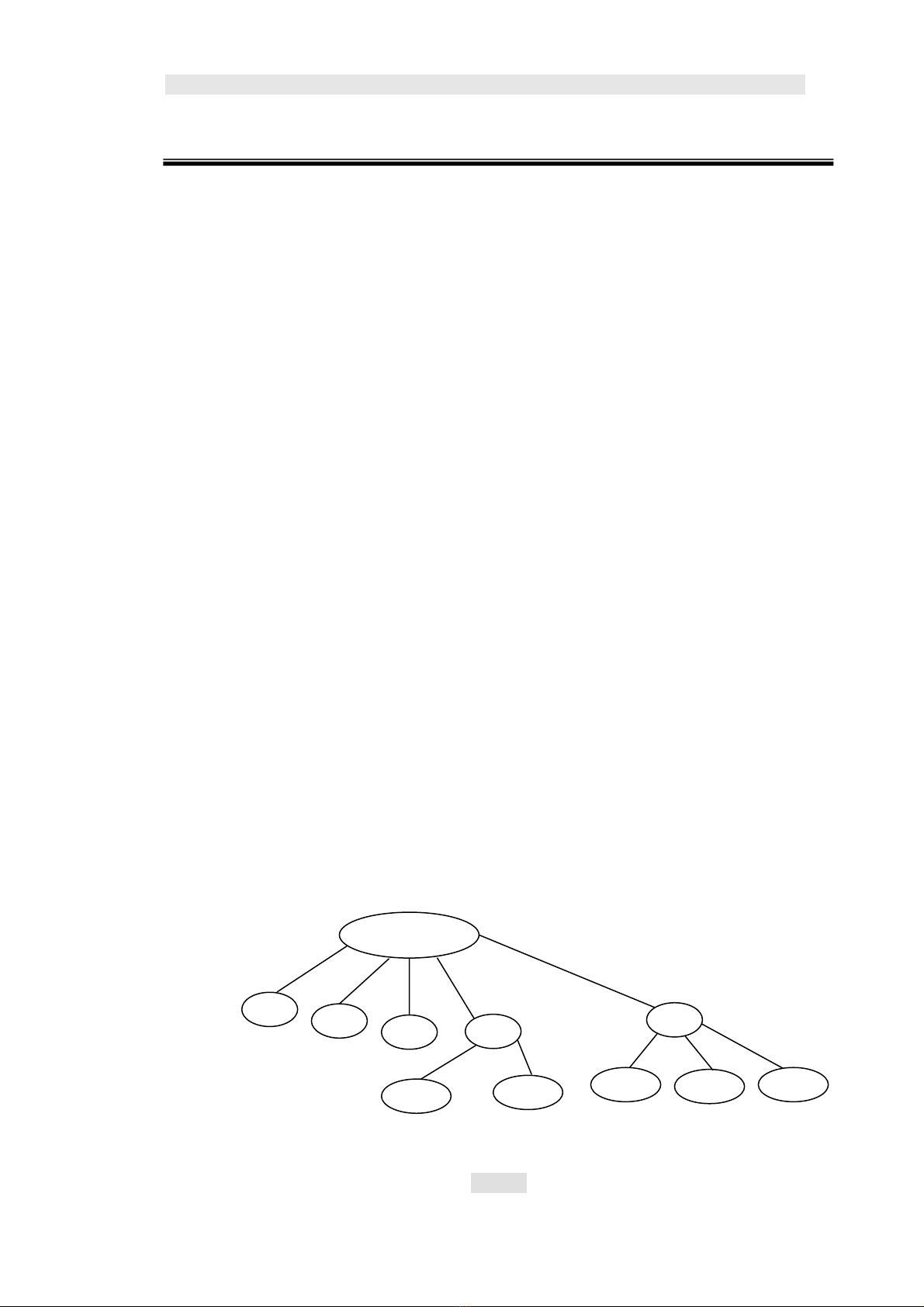
Ví dụ : Chương 1 của giáo trình có cấu trúc cây.
1. Giải thuật
1.1. Cấu trúc dữ liệu và giải thuật
1.2. Ngôn ngữ diễn đạt giải thuật
1.3. Thiết kế giải thuật
1.4. Đánh giá giải thuật
1.4.1. Đặt vấn đề
1.4.2. Thời gian thực hiện trung bình
1.5. Giải thuật đệ quy
1.5.1. Ví dụ về thủ tục đệ quy
1.5.2. Chú ý
Cây này có thể biển diễn như hình 5.1
Chương1
1.
1.
1.
1.
1.4.
1.4.
1.
1.5.
1.5.
1.5.
Hình 5.1

Giáo trình Cấu trúc dữ liệu Trường THCN Công - Kỹ Nghệ Ðông Á
Trang 2
Sau đây là 1 số khái niệm :
a) Số các con của 1 nút được
gọi là
cấp (degree) của 1 nút đó. Nút có cấp
bằng 0 gọi là lá (leaf) hay nút tận
cùng (termina node). Nút không phải
là lá được gọi là nút nhánh (branch
node).
Cấp cao nhất của nút trên cây được
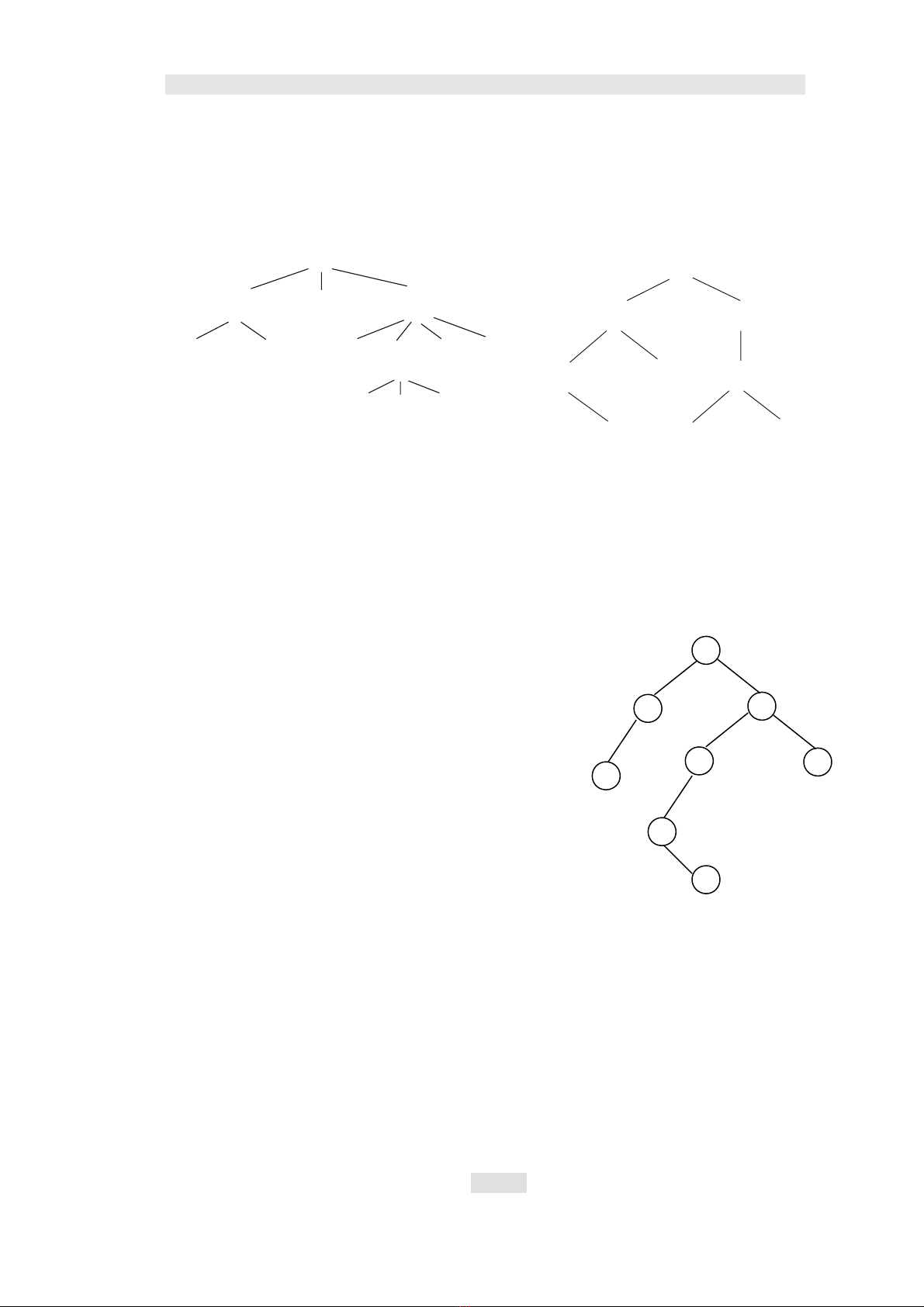
gọi là cấp của cây đó. Ví dụ : với cây
ở hình 5.2 (ở đây các chữ A, B,
C,…tựơng trưng cho phần thông tin
(dữ liệu) ứng với mỗi nút).
A là gốc ; B, C, D là con của A ; D là cha của G, H, I, J ; A có cấp bằng 3,
D có cấp bằng 4. Các nút như E, F, C, G, K,…là lá. Các nút như B, D, H…là các
nút nhánh. Cây trên có cấp bằng 4.
b) Gốc của cây có mức (level) bằng 1.
Nếu nút cha có mức là i thì nút con có mức là i + 1.
Như ở cây trên :
A có mức là 1 ;
B, C, D có mức là 2 ;
E, F, G, I, J có mức là 3 ;
K, L, M có mức là 4.
c) Chiều cao (height) hay chiều sâu (depth) của 1 cây là số mức lớn nhất
của nút có trên cây đó.
Cây ở hình 5.1 có chiều cao là 3
Cây ở hình 5.2 có chiều cao là 4
d) Nếu n1, n2 ,…,nk là dãy các nút mà ni là cha của ni+1 với 1≤ i ≤ k thì dãy
đó được gọi là đường đi (path) từ n1 đến nk.Độ dài của đuờng đi (path length)
bằng số nút trên đường đi đó trừ đi 1. Ví dụ với cây ở hình 5.2 : độ dài đường đi
từ A đến L bằng 3, độ dài đường đi từ D tới M.
e) Nếu thứ tự các cây con của 1 nút được coi trọng thì cây đang xét là cây
có thứ tự (ordered tree), ngược lại là cây không có thứ tự (unordered tree).
f) Đối với nút trên cây ngoài khái niệm cha, con, người ta còn có thể mở
sang các khái niệm khác theo quan hệ như trong gia tộc. Ví dụ như trong hình
5.2 . A, D, H … được gọi là tiền bối của L ; còn E, G, K… được gọi là hậu sinh
của A…; các nút G, H, I, J là các nút anh em v.v…
A
B
C
D
F
G
H
I
J
E
K
L
F
Hình 5.2
Giáo trình Cấu trúc dữ liệu Trường THCN Công - Kỹ Nghệ Ðông Á
Trang 3
Chú ý. Đôi lúc, để cho tiện, hình vẽ minh hoạ của cây sẽ được thể hiện đơn
giản : nút trên cây chỉ tượng trưng bằng chữ hoặc số.
Ví dụ như cây ở hình 5.2, có thể minh hoạ bởi 5.3. Hoặc cây mà mỗi nút
đều chứa 1 số như hình 5.4.
II. CÂY NHỊ PHÂN
1. Định nghĩa
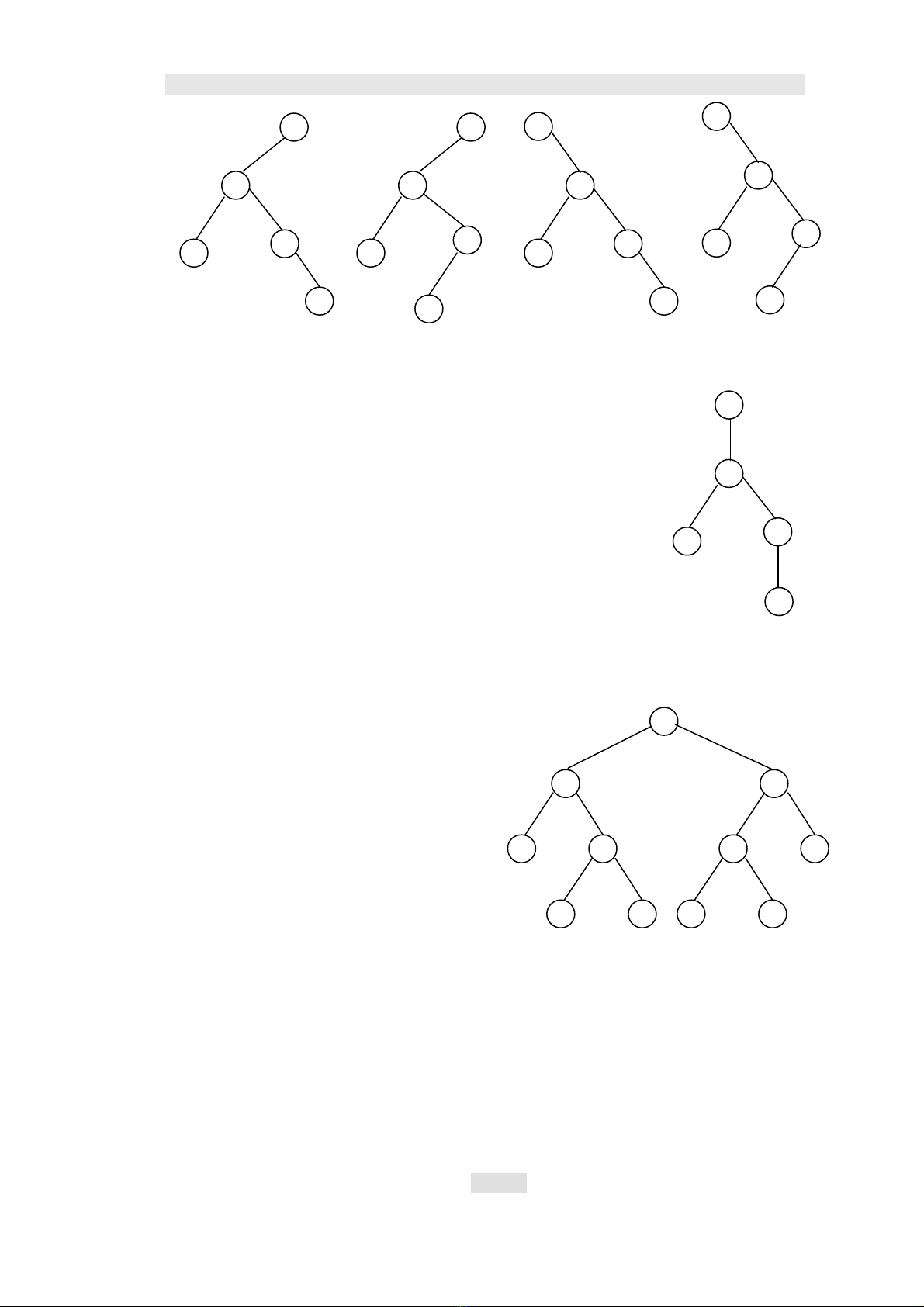
Cây nhị phân là 1 dạng quan trọng của cấu trúc cây.Nó có đặc điểm là : mọi
nút trên cây chỉ có tối đa là 2 con. Đối với cây con
của mỗi nút thì cũng phân biệt cây con trái (left
subtree) và cây con phải (right subtree).
Như vậy cây nhị phân là 1 cây có thứ tự. Ví
dụ : cây trên hình 5.5 là 1 cây nhị phân có A là nút
gốc, cây con trái của A có gốc là B, cây con phải
của A có gốc là C.
Các cây trên hình 5.6 là các cây nhị phân
khác nhau.
A
B
D
E
C
G
H
F
Hình 5.5
Hình 5.3
Hình 5.4
A
B
C
D
E
Ì
G
H
I
J
K
L
M
14
17
2
1
9
5
3
13
4
4
39
68
Giáo trình Cấu trúc dữ liệu Trường THCN Công - Kỹ Nghệ Ðông Á
Trang 4
A
B
C
D
E
Hình 5.7
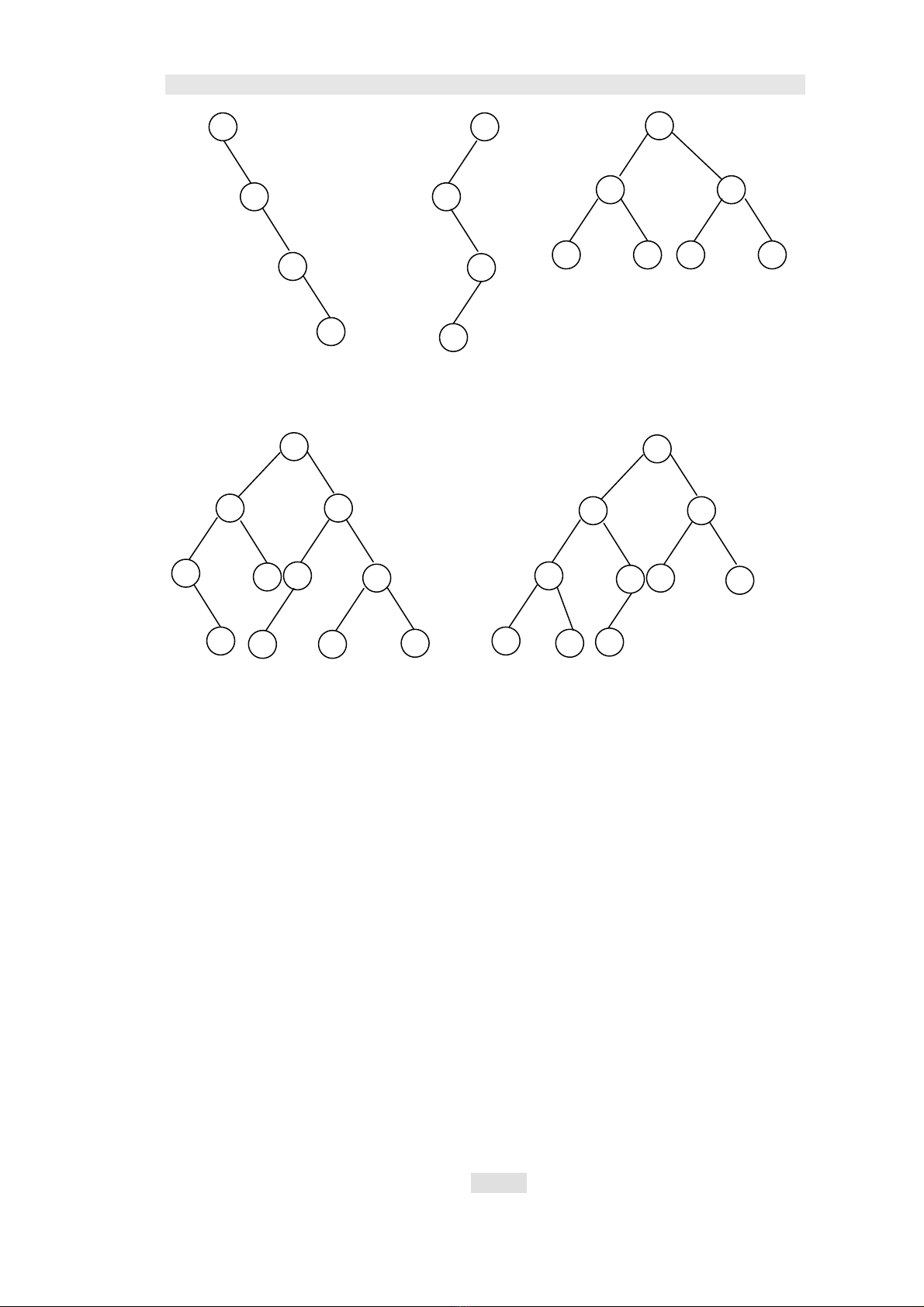
Chẳng hạn : cây a) khác cây b) vì với a) E là con phải
của D, còn với b) thì E lại là con trái của D, cây a) khác cây
c) vì với c) B không phải là con trái mà là con phải của A
Nếu không để ý tới thứ tự của cây con thì cả 4 cây nêu
trên, đều chỉ là 1, mà có thể minh hoạ bởi hình 5.7:
Có rất nhiều đối tượng có thể biểu diễn theo cấu trúc
cây nhị phân, chẳng hạn :
− Biểu thức số hạng với phép
toán 2 ngôi nếu coi toán tử là ứng
với gốc, toán hạng 1 ứng với cây
con trái, toán hạng 2 ứng với cây
con phải, thì có thể biểu diễn bởi
cây nhị phân.Chẳng hạn :
(x – 2 ∗ y) + (y / z) ↑ 3
Có thể biểu diễn như sau :
Cần chú ý tới một số dạng đặc biệt của cây nhị phân tương tự như ở hình
5.8.
Các cây như hình 5.8 a, b đựơc gọi là cây suy biến (degenerate linary tree),
trên đó, C trừ nút lá, các nút nhánh đều chỉ có 1 con.
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
a) b) c) d)
Hình 5.6
-
+
*
x
↑
3
/
y
2
z
y
Giáo trình Cấu trúc dữ liệu Trường THCN Công - Kỹ Nghệ Ðông Á
Trang 5
A
C
G
K
Hình 5.8d,e)
d)
e)
B
E
D
H
F
I
J
A
C
G
B
E
D
I
F
H
J
Cây ở hình 5.8c được gọi là cây đầy đủ (full tree), trên đó trừ nút lá các nút
nhánh đều có 2 con hay nói 1 cách khác : số nút ở mọi mức trên cây đều “đầy đủ”
cả.
Cây ở hình 5.8d có số nút đầy đủ ở mọi mức, trừ ở mức cuối cùng. Ta sẽ gọi
là cây gần đầy .
Nếu cây gần đầy mà ở mức cuối cùng các nút đều dạt về phía trái, như cây
hình 5.8e thì được gọi là cây hoàn chỉnh.
2. Tính chất
Bây giờ ta sẽ xét tới 1 vài tính chất đặc biệt của cây nhị phân, qua bổ đề sau
đây :
Bổ đề:
1) Số lượng tối đa của các nút ở mức i trên cây nhị phân là 2i-1 (i ≥ 1) .
2) Số lượng tối đa của các nút trên 1 cây nhị phân có chiều cao h là 2h – 1
(h≥ 1).
A
B
B
C
D
Hình 5.8a,b,c)
A
C
D
B
A
E
D
C
G
F
a)
b)
c)


























