www.vnmath.com
Bµi 1 : CH NG MINH M T S KHÔNG PH I LÀ S CHÍNHỨ Ộ Ố Ả Ố
PH NGƯƠ
Trong ch ng trình Toán l p 6, các em đã đ c h c v các bài toán liên quan t i phép chiaươ ớ ượ ọ ề ớ
h t c a m t s t nhiên cho m t s t nhiên khác 0 và đ c bi t là đ c gi i thi u v s chínhế ủ ộ ố ự ộ ố ự ặ ệ ượ ớ ệ ề ố
ph ng, đó là s t nhiên b ng bình ph ng c a m t s t nhiên (ch ng h n : 0 ; 1 ; 4 ; 9 ;16 ; 25 ;ươ ố ự ằ ươ ủ ộ ố ự ẳ ạ
121 ; 144 ; …).
K t h p các ki n th c trên, các em có th gi i quy t bài toán : Ch ng minh m t s khôngế ợ ế ứ ể ả ế ứ ộ ố
ph i là s chính ph ng. Đây cũng là m t cách c ng c các ki n th c mà các em đã đ c h c.ả ố ươ ộ ủ ố ế ứ ượ ọ
Nh ng bài toán này s làm tăng thêm lòng say mê môn toán cho các em. ữ ẽ
1. Nhìn ch s t n cùngữ ố ậ
Vì s chính ph ng b ng bình ph ng c a m t s t nhiên nên có th th y ngay ố ươ ằ ươ ủ ộ ố ự ể ấ s chính ph ngố ươ
ph i có ch s t n cùng là m t trong các ch s 0 ; 1 ; 4 ; 5 ; 6 ; 9.ả ữ ố ậ ộ ữ ố T đó các em có th gi iừ ể ả
đ c bài toán ki u sau đây : ượ ể
Bài toán 1 : Ch ng minh s : n = 2004ứ ố 2 + 20032 + 20022 - 20012 không ph i là s chínhả ố
ph ng. ươ
L i gi i :ờ ả D dàng th y ch s t n cùng c a các s 20042 ; 20032 ; 20022 ; 20012 l n l tễ ấ ữ ố ậ ủ ố ầ ượ
là 6 ; 9 ; 4 ; 1. Do đó s n có ch s t n cùng là 8 nên n không ph i là s chính ph ng. ố ữ ố ậ ả ố ươ
Chú ý : Nhi u khi s đã cho có ch s t n cùng là m t trong các s 0 ; 1 ; 4 ; 5 ; 6 ; 9 nh ngề ố ữ ố ậ ộ ố ư
v n không ph i là s chính ph ng. Khi đó các b n ph i l u ý thêm m t chút n a : ẫ ả ố ươ ạ ả ư ộ ữ
N u s chính ph ng chia h t cho s nguyên t p thì ph i chia h t cho pế ố ươ ế ố ố ả ế 2.
Bài toán 2 : Ch ng minh s 1234567890 không ph i là s chính ph ng. ứ ố ả ố ươ
L i gi i :ờ ả Th y ngay s 1234567890 chia h t cho 5 (vì ch s t n cùng là 0) nh ng khôngấ ố ế ữ ố ậ ư
chia h t cho 25 (vì hai ch s t n cùng là 90). Do đó s 1234567890 không ph i là s chính ph ng.ế ữ ố ậ ố ả ố ươ
Chú ý : Có th lý lu n 1234567890 chia h t cho 2 (vì ch s t n cùng là 0), nh ng khôngể ậ ế ữ ố ậ ư
chia h t cho 4 (vì hai ch s t n cùng là 90) nên 1234567890 không là s chính ph ng. ế ữ ố ậ ố ươ
Bài toán 3 : Ch ng minh r ng n u m t s có t ng các ch s là 2004 thì s đó không ph i làứ ằ ế ộ ố ổ ữ ố ố ả
s chính ph ng. ố ươ
L i gi i : Ta th y t ng các ch s c a s 2004 là 6 nên 2004 chia h t cho 3 mà không chiaờ ả ấ ổ ữ ố ủ ố ế
h t 9 nên s có t ng các ch s là 2004 cũng chia h t cho 3 mà không chia h t cho 9, do đó s nàyế ố ổ ữ ố ế ế ố
không ph i là s chính ph ng. ả ố ươ
2. Dùng tính ch t c a s dấ ủ ố ư
Ch ng h n các em g p bài toán sau đây : ẳ ạ ặ
Bài toán 4 : Ch ng minh m t s có t ng các ch s là 2006 không ph i là s chính ph ng. ứ ộ ố ổ ữ ố ả ố ươ
Ch c ch n các em s d b “choáng”. V y bài toán này ta s ph i nghĩ t i đi u gì ? Vì choắ ắ ẽ ễ ị ậ ở ẽ ả ớ ề
gi thi t v t ng các ch s nên ch c ch n các em ph i nghĩ t i phép chia cho 3 ho c cho 9. Nh ngả ế ề ổ ữ ố ắ ắ ả ớ ặ ư
l i không g p đi u “kì di u” nh bài toán 3. Th thì ta nói đ c đi u gì v s này ? Ch c ch n sạ ặ ề ệ ư ế ượ ề ề ố ắ ắ ố
này chia cho 3 ph i d 2. T đó ta có l i gi i. ả ư ừ ờ ả
L i gi i :ờ ả Vì s chính ph ng khi chia cho 3 ch có s d là 0 ho c 1ố ươ ỉ ố ư ặ mà thôi (coi nh bàiư
t p đ các em t ch ng minh !). Do t ng các ch s c a s đó là 2006 nên s đó chia cho 3 d 2.ậ ể ự ứ ổ ữ ố ủ ố ố ư
Ch ng t s đã cho không ph i là s chính ph ng. ứ ỏ ố ả ố ươ
T ng t các em có th t gi i quy t đ c 2 bài toán : ươ ự ể ự ả ế ượ
Bài toán 5 : Ch ng minh t ng các s t nhiên liên ti p t 1 đ n 2005 không ph i là s chínhứ ổ ố ự ế ừ ế ả ố
ph ng. ươ
Bài toán 6 : Ch ng minh s : n = 2004ứ ố 4 + 20043 + 20042 + 23 không là s chính ph ng. ố ươ
Bây gi các em theo dõi bài toán sau đ nghĩ t i m t “tình hu ng” m i. ờ ể ớ ộ ố ớ
Bài toán 7 : Ch ng minh s :ứ ố
n = 44 + 4444 + 444444 + 44444444 + 15 không là s chính ph ng.ố ươ
GV : NguyÔn Thanh H¶i - Trêng THCS Lª §×nh Kiªn 1
www.vnmath.com
Nh n xét :ậ N u xét n chia cho 3, các em s th y s d c a phép chia s là 1, th là khôngế ẽ ấ ố ư ủ ẽ ế
“b t ch c” đ c cách gi i c a các bài toán 3 ; 4 ; 5 ; 6. N u xét ch s t n cùng các em s th yắ ướ ượ ả ủ ế ữ ố ậ ẽ ấ
ch s t n cùng c a n là 9 nên không làm “t ng t ” đ c nh các bài toán 1 ; 2. S d c a phépữ ố ậ ủ ươ ự ượ ư ố ư ủ
chia n cho 4 là d th y nh t, đó chính là 3. M tễ ấ ấ ộ s chính ph ng khi chia cho 4 s cho s d nhố ươ ẽ ố ư ư
th nào nh ?ế ỉ Các em có th t ch ng minh và đ c k t qu : s d đó ch có th làể ự ứ ượ ế ả ố ư ỉ ể 0 ho c 1ặ. Như
v y là các em đã gi i xong bài toán 7. ậ ả
3. “K p” s gi a hai s chính ph ng “liên ti p”ẹ ố ữ ố ươ ế
Các em có th th y r ng : N u n là s t nhiên và s t nhiên k th a mãn nể ấ ằ ế ố ự ố ự ỏ 2 < k < (n + 1)2 thì
k không là s chính ph ng. T đó các em có th xét đ c các bài toán sau : ố ươ ừ ể ượ
Bài toán 8 : Ch ng minh s 4014025 không là s chính ph ng. ứ ố ố ươ
Nh n xét :ậ S này có hai ch s t n cùng là 25, chia cho 3 d 1, chia cho 4 cũng d 1. Th làố ữ ố ậ ư ư ế
t t c các cách làm tr c đ u không v n d ng đ c. Các em có th th y l i gi i theo m t h ngấ ả ướ ề ậ ụ ượ ể ấ ờ ả ộ ướ
khác.
L i gi i :ờ ả Ta có 20032 = 4012009 ; 20042 = 4016016 nên 20032 < 4014025 < 20042. Ch ng tứ ỏ
4014025 không là s chính ph ng. ố ươ
Bài toán 9 : Ch ng minh A = n(n + 1)(n + 2)(n + 3) không là s chính ph ng v i m i s tứ ố ươ ớ ọ ố ự
nhiên n khác 0.
Nh n xét :ậ Đ i v i các em đã làm quen v i d ng bi u th c này thì có th nh n ra A + 1 làố ớ ớ ạ ể ứ ể ậ
s chính ph ng (đây là bài toán quen thu c v i l p 8). Các em l p 6, l p 7 cũng có th ch u khóố ươ ộ ớ ớ ớ ớ ể ị
đ c l i gi i. ọ ờ ả
L i gi i :ờ ả Ta có :
A + 1 = n(n + 1)(n + 2)(n + 3) + 1 = (n2 + 3n)(n2 + 3n + 2) + 1 = (n2 + 3n)2 + 2(n2 + 3n) +1 = (n2
+ 3n +1)2.
M t khác : ặ
(n2 + 3n)2 < (n2 + 3n)2 + 2(n2 + 3n) = A.
Đi u này hi n nhiên đúng vì n ≥ 1. Ch ng t : (nề ể ứ ỏ 2 + 3n)2 < A < A + 1 = (n2 + 3n +1)2. => A không là
s chính ph ng. ố ươ
Các em có th rèn luy n b ng cách th gi i bài toán sau : ể ệ ằ ử ả
Bài toán 10 : Hãy tìm s t nhiên n sao cho A = nố ự 4 - 2n3 + 3n2 - 2n là s chính ph ng. ố ươ
G i ý : Nghĩ đ n (nợ ế 2 - n + 1)2.
Bài toán 11 : Ch ng minh s 23ứ ố 5 + 2312 + 232003 không là s chính ph ng. ố ươ
G i ý : Nghĩ đ n phép chia cho 3 ho c phép chia cho 4. ợ ế ặ
Bài toán 12 : Có 1000 m nh bìa hình ch nh t, trên m i m nh bìa đ c ghi m t s trong cácả ữ ậ ỗ ả ượ ộ ố
s t 2 đ n 1001 sao cho không có hai m nh nào ghi s gi ng nhau. Ch ng minh r ng : Không thố ừ ế ả ố ố ứ ằ ể
ghép t t c các m nh bìa này li n nhau đ đ c m t s chính ph ng. ấ ả ả ề ể ượ ộ ố ươ
Bài toán 13 : Ch ng minh r ng : T ng các bình ph ng c a b n s t nhiên liên ti p khôngứ ằ ổ ươ ủ ố ố ự ế
th là s chính ph ng. ể ố ươ
G i ý : Nghĩ t i phép chia cho 4. ợ ớ
Bài toán 14 : Ch ng minh r ng s 333ứ ằ ố 333 + 555555 + 777777 không là s chính ph ng. ố ươ
G i ý : Nghĩ đ n phép chia cho … m t ch c (?) ợ ế ộ ụ
Bài toán 15 : Lúc đ u có hai m nh bìa, m t c u bé tinh ngh ch c c m m t m nh bìa lên l iầ ả ộ ậ ị ứ ầ ộ ả ạ
xé ra làm b n m nh. C u ta mong r ng c làm nh v y đ n m t lúc nào đó s đ c s m nh bìa làố ả ậ ằ ứ ư ậ ế ộ ẽ ượ ố ả
m t s chính ph ng. C u ta có th c hi n đ c mong mu n đó không ? ộ ố ươ ậ ự ệ ượ ố
Đ k t thúc bài vi t này, tôi mu n chúc các em h c th t gi i môn toán ngay t đ u b c THCS vàể ế ế ố ọ ậ ỏ ừ ầ ậ
cho tôi đ c nói riêng v i các quý th y cô : nguyên t c chung đ ch ng minh m t s t nhiên khôngượ ớ ầ ắ ể ứ ộ ố ự
là s chính ph ng, đó là d a vào m t trong các đi u ki n c n đ m t s là s chính ph ng (màố ươ ự ộ ề ệ ầ ể ộ ố ố ươ
nh các quý th y cô đã bi t : m i đi u ki n c n trên đ i là dùng đ … ph đ nh !). T đó các quýư ầ ế ọ ề ệ ầ ờ ể ủ ị ừ
th y cô có th sáng t o thêm nhi u bài toán thú v khác. ầ ể ạ ề ị
GV : NguyÔn Thanh H¶i - Trêng THCS Lª §×nh Kiªn 2
www.vnmath.com
Bµi 2 : CH NG MINH M T S LÀ S CHÍNH PH NGỨ Ộ Ố Ố ƯƠ
Các b n đã đ c gi i thi u các ph ng pháp ch ng minh m t s không ph i là s chínhạ ượ ớ ệ ươ ứ ộ ố ả ố
ph ng trong TTT2 s 9. Bài vi t này, tôi mu n gi i thi u v i các b n bài toán ch ng minh m t sươ ố ế ố ớ ệ ớ ạ ứ ộ ố
là s chính ph ng. ố ươ
Ph ng pháp 1 : D a vào đ nh nghĩa. ươ ự ị
Ta bi t r ng, s chính ph ng là bình ph ng c a m t s t nhiên. D a vào đ nh nghĩa này,ế ằ ố ươ ươ ủ ộ ố ự ự ị
ta có th đ nh h ng gi i quy t các bài toán. ể ị ướ ả ế
Bài toán 1 : Ch ng minh : V i m i s t nhiên n thì aứ ớ ọ ố ự n = n(n + 1)(n + 2)(n + 3) + 1 là số
chính ph ng. ươ
L i gi i :ờ ả Ta có :
an = n(n + 1) (n + 2) (n + 3) + 1
= (n2 + 3n) (n2 + 3n + 2) + 1
= (n2 + 3n)2 + 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
V i n là s t nhiên thì nớ ố ự 2 + 3n + 1 cũng là s t nhiên, theo đ nh nghĩa, aố ự ị n là s chính ph ng. ố ươ
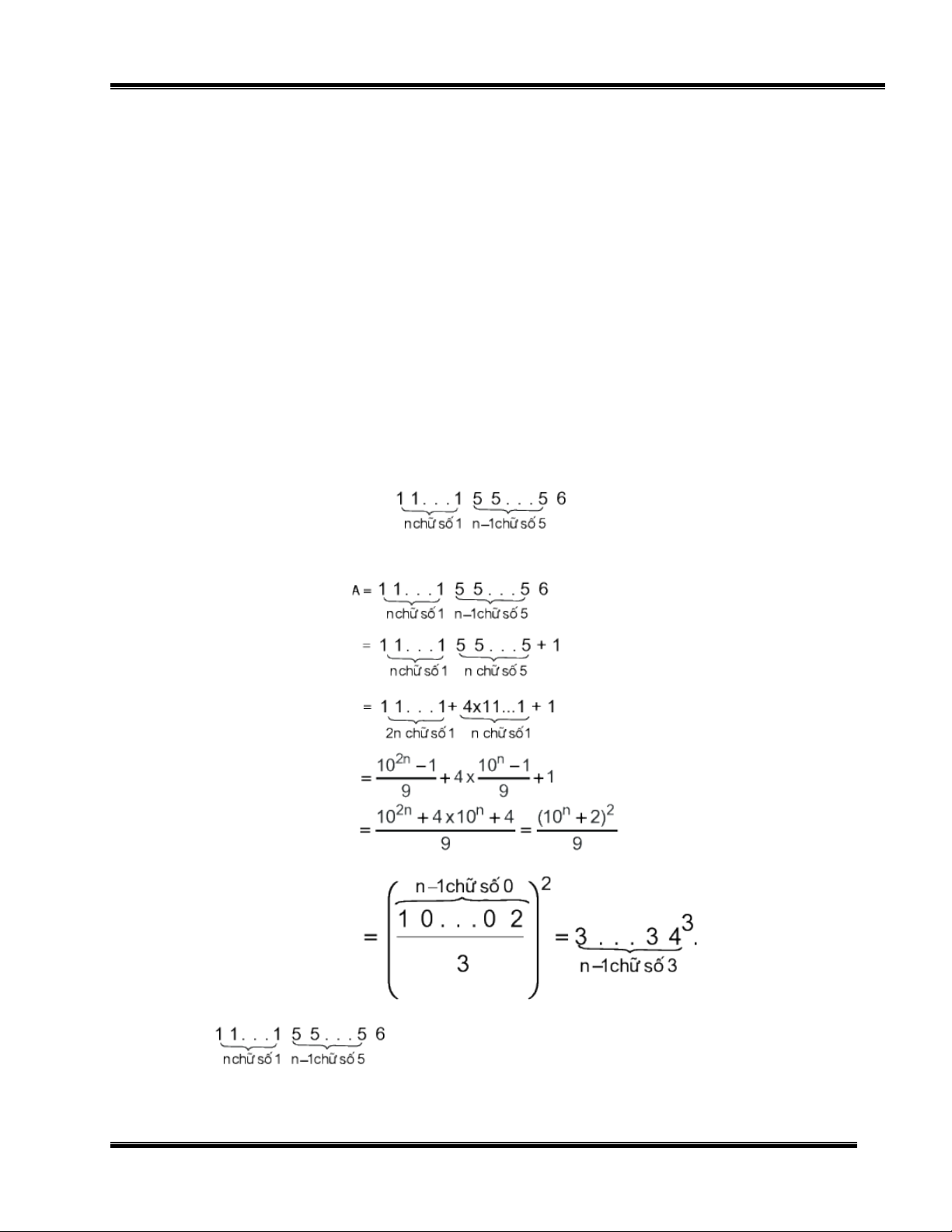
Bài toán 2 : Ch ng minh s : ứ ố là s chính ph ng. ố ươ
L i gi i :ờ ả
Ta có :
V y : ậlà s chính ph ng. ố ươ
Ph ng pháp 2 : D a vào tính ch t đ c bi t.ươ ự ấ ặ ệ
Ta có th ch ng minh m t tính ch t r t đ c bi t : “N u a, b là hai s t nhiên nguyên tể ứ ộ ấ ấ ặ ệ ế ố ự ố
cùng nhau và a.b là m t s chính ph ng thì a và b đ u là các s chính ph ng”.ộ ố ươ ề ố ươ
GV : NguyÔn Thanh H¶i - Trêng THCS Lª §×nh Kiªn 3
www.vnmath.com
Bài toán 3 : Ch ng minh r ng : N u m, n là các s t nhiên th a mãn 3mứ ằ ế ố ự ỏ 2 + m = 4n2 + n thì m
- n và 4m + 4n + 1 đ u là s chính ph ng.ề ố ươ
L i gi i :ờ ả
Ta có : 3m2 + m = 4n2 + n
t ng đ ng v i 4(mươ ươ ớ 2 - n2) + (m - n) = m2
hay là (m - n)(4m + 4n + 1) = m2 (*)
G i d là c chung l n nh t c a m - n và 4m + 4n + 1 thì (4m + 4n + 1) + 4(m - n) chia h t cho d =>ọ ướ ớ ấ ủ ế
8m + 1 chí h t cho d. ế
M t khác, t (*) ta có : mặ ừ 2 chia h t cho dế2 => m chia h t cho d. ế
T 8m + 1 chia h t cho d và m chia h t cho d ta có 1 chia h t cho d => d = 1. ừ ế ế ế
V y m - n và 4m + 4n + 1 là các s t nhiên nguyên t cùng nhau, th a mãn (*) nên chúng đ u là cácậ ố ự ố ỏ ề
s chính ph ng. Cu i cùng xin g i t i các b n m t s bài toán thú v v s chính ph ng :ố ươ ố ử ớ ạ ộ ố ị ề ố ươ
1) Ch ng minh các s sau đây là s chính ph ng : ứ ố ố ươ
2) Cho các s nguyên d ng a, b, c đôi m t nguyên t cùng nhau, th a mãn : 1/a + 1/b = 1/c. Hãy choố ươ ộ ố ỏ
bi t a + b có là s chính ph ng hay không ? ế ố ươ
3) Ch ng minh r ng, v i m i s t nhiên n thì 3ứ ằ ớ ọ ố ự n + 4 không là s chính ph ng. ố ươ
4) Tìm s t nhiên n đ nố ự ể 2 + 2n + 2004 là s chính ph ng.ố ươ
5) Ch ng minh : N u : ứ ế và n là hai s t nhiên thì a là s chính ph ng. ố ự ố ươ
Bµi 3 : TÌM CH S T N CÙNGỮ Ố Ậ
Tìm ch s t n cùng c a m t s t nhiên là d ng toán hay. Đa s các tài li u v d ng toánữ ố ậ ủ ộ ố ự ạ ố ệ ề ạ
này đ u s d ng khái ni m đ ng d , m t khái ni m tr u t ng và không có trong ch ng trình. Vìề ử ụ ệ ồ ư ộ ệ ừ ượ ươ
th có không ít h c sinh, đ c bi t là các b n l p 6 và l p 7 khó có th hi u và ti p thu đ c. ế ọ ặ ệ ạ ớ ớ ể ể ế ượ
Qua bài vi t này, tôi xin trình bày v i các b n m t s tính ch t và ph ng pháp gi i bài toán “tìmế ớ ạ ộ ố ấ ươ ả
ch s t n cùng”, ch s d ng ki n th c THCS.ữ ố ậ ỉ ử ụ ế ứ
Chúng ta xu t phát t tính ch t sau : ấ ừ ấ
Tính ch t 1 :ấ
a) Các s có ch s t n cùng là 0, 1, 5, 6 khi nâng lên lũy th a b c b t kì thì ch s t n cùngố ữ ố ậ ừ ậ ấ ữ ố ậ
v n không thay đ i. ẫ ổ
b) Các s có ch s t n cùng là 4, 9 khi nâng lên lũy th a b c l thì ch s t n cùng v nố ữ ố ậ ừ ậ ẻ ữ ố ậ ẫ
không thay đ i. ổ
c) Các s có ch s t n cùng là 3, 7, 9 khi nâng lên lũy th a b c 4n (n thu c N) thì ch số ữ ố ậ ừ ậ ộ ữ ố
t n cùng là 1. ậ
d) Các s có ch s t n cùng là 2, 4, 8 khi nâng lên lũy th a b c 4n (n thu c N) thì ch số ữ ố ậ ừ ậ ộ ữ ố
t n cùng là 6.ậ
Vi c ch ng minh tính ch t trên không khó, xin dành cho b n đ c. Nh v y, mu n tìm ch s t nệ ứ ấ ạ ọ ư ậ ố ữ ố ậ
cùng c a s t nhiên x = aủ ố ự m, tr c h t ta xác đ nh ch s t n cùng c a a. ướ ế ị ữ ố ậ ủ
- N u ch s t n cùng c a a là 0, 1, 5, 6 thì x cũng có ch s t n cùng là 0, 1, 5, 6. ế ữ ố ậ ủ ữ ố ậ
- N u ch s t n cùng c a a là 3, 7, 9, vì aế ữ ố ậ ủ m = a4n + r = a4n.ar v i r = 0, 1, 2, 3 nên t tính ch t 1c =>ớ ừ ấ
ch s t n cùng c a x chính là ch s t n cùng c a aữ ố ậ ủ ữ ố ậ ủ r.
- N u ch s t n cùng c a a là 2, 4, 8, cũng nh tr ng h p trên, t tính ch t 1d => ch s t n cùngế ữ ố ậ ủ ư ườ ợ ừ ấ ữ ố ậ
c a x chính là ch s t n cùng c a 6.aủ ữ ố ậ ủ r.
GV : NguyÔn Thanh H¶i - Trêng THCS Lª §×nh Kiªn 4
www.vnmath.com
Bài toán 1 : Tìm ch s t n cùng c a các s : ữ ố ậ ủ ố
a) 799 b) 141414 c) 4567
L i gi i : ờ ả
a) Tr c h t, ta tìm s d c a phép chia 99 cho 4 : ướ ế ố ư ủ
99 - 1 = (9 - 1)(98 + 97 + … + 9 + 1) chia h t cho 4 ế
=> 99 = 4k + 1 (k thu c N) => 7ộ99 = 74k + 1 = 74k.7
Do 74k có ch s t n cùng là 1 (theo tính ch t 1c) => 7ữ ố ậ ấ 99 có ch s t n cùng là 7.ữ ố ậ
b) D th y 14ễ ấ 14 = 4k (k thu c N) => theo tính ch t 1d thì 14ộ ấ 1414 = 144k có ch s t n cùng là 6. ữ ố ậ
c) Ta có 567 - 1 chia h t cho 4 => 5ế67 = 4k + 1 (k thu c N) ộ
=> 4567 = 44k + 1 = 44k.4, theo tính ch t 1d, 4ấ4k có ch s t n cùng là 6 nên 4ữ ố ậ 567 có ch s t n cùng là 4. ữ ố ậ
Tính ch t sau đ c => t tính ch t 1. ấ ượ ừ ấ
Tính ch t 2 : ấM t s t nhiên b t kì, khi nâng lên lũy th a b c 4n + 1 (n thu c N) thì ch sộ ố ự ấ ừ ậ ộ ữ ố
t n cùng v n không thay đ i.ậ ẫ ổ
Ch s t n cùng c a m t t ng các lũy th a đ c xác đ nh b ng cách tính t ng các ch s t n cùngữ ố ậ ủ ộ ổ ừ ượ ị ằ ổ ữ ố ậ
c a t ng lũy th a trong t ng. ủ ừ ừ ổ
Bài toán 2 : Tìm ch s t n cùng c a t ng S = 2ữ ố ậ ủ ổ 1 + 35 + 49 + … + 20048009.
L i gi i : ờ ả
Nh n xét :ậ M i lũy th a trong S đ u có s mũ khi chia cho 4 thì d 1 (các lũy th a đ u có d ng nọ ừ ề ố ư ừ ề ạ 4(n -
2) + 1, n thu c {2, 3, …, 2004}). ộ
Theo tính ch t 2, m i lũy th a trong S và các c s t ng ng đ u có ch s t n cùng gi ng nhau,ấ ọ ừ ơ ố ươ ứ ề ữ ố ậ ố
b ng ch s t n cùng c a t ng : ằ ữ ố ậ ủ ổ
(2 + 3 + … + 9) + 199.(1 + 2 + … + 9) + 1 + 2 + 3 + 4 = 200(1 + 2 + … + 9) + 9 = 9009.
V y ch s t n cùng c a t ng S là 9. ậ ữ ố ậ ủ ổ
T tính ch t 1 ti p t c => tính ch t 3. ừ ấ ế ụ ấ
Tính ch t 3 :ấ
a) S có ch s t n cùng là 3 khi nâng lên lũy th a b c 4n + 3 s có ch s t n cùng là 7 ;ố ữ ố ậ ừ ậ ẽ ữ ố ậ
s có ch s t n cùng là 7 khi nâng lên lũy th a b c 4n + 3 s có ch s t n cùng là 3. ố ữ ố ậ ừ ậ ẽ ữ ố ậ
b) S có ch s t n cùng là 2 khi nâng lên lũy th a b c 4n + 3 s có ch s t n cùng là 8 ;ố ữ ố ậ ừ ậ ẽ ữ ố ậ
s có ch s t n cùng là 8 khi nâng lên lũy th a b c 4n + 3 s có ch s t n cùng là 2. ố ữ ố ậ ừ ậ ẽ ữ ố ậ
c) Các s có ch s t n cùng là 0, 1, 4, 5, 6, 9, khi nâng lên lũy th a b c 4n + 3 s khôngố ữ ố ậ ừ ậ ẽ
thay đ i ch s t n cùng. ổ ữ ố ậ
Bài toán 3 : Tìm ch s t n cùng c a t ng T = 2ữ ố ậ ủ ổ 3 + 37 + 411 + … + 20048011.
L i gi i : ờ ả
Nh n xét :ậ M i lũy th a trong T đ u có s mũ khi chia cho 4 thì d 3 (các lũy th a đ u có d ng nọ ừ ề ố ư ừ ề ạ 4(n -
2) + 3, n thu c {2, 3, …, 2004}). ộ
Theo tính ch t 3 thì 2ấ3 có ch s t n cùng là 8 ; 3ữ ố ậ 7 có ch s t n cùng là 7 ; 4ữ ố ậ 11 có ch s t n cùng làữ ố ậ
4 ; …
Nh v y, t ng T có ch s t n cùng b ng ch s t n cùng c a t ng : (8 + 7 + 4 + 5 + 6 + 3 + 2 + 9)ư ậ ổ ữ ố ậ ằ ữ ố ậ ủ ổ
+ 199.(1 + 8 + 7 + 4 + 5 + 6 + 3 + 2 + 9) + 1 + 8 + 7 + 4 = 200(1 + 8 + 7 + 4 + 5 + 6 + 3 + 2 + 9) + 8 +
7 + 4 = 9019.
V y ch s t n cùng c a t ng T là 9. ậ ữ ố ậ ủ ổ
* Trong m t s bài toán khác, vi c tìm ch s t n cùng d n đ n l i gi i khá đ c đáo. ộ ố ệ ữ ố ậ ẫ ế ờ ả ộ
Bài toán 4 : T n t i hay không s t nhiên n sao cho nồ ạ ố ự 2 + n + 1 chia h t cho 1995ế2000.
L i gi i :ờ ả 19952000 t n cùng b i ch s 5 nên chia h t cho 5. Vì v y, ta đ t v n đ là li u nậ ở ữ ố ế ậ ặ ấ ề ệ 2
+ n + 1 có chia h t cho 5 không ? ế
Ta có n2 + n = n(n + 1), là tích c a hai s t nhiên liên ti p nên ch s t n cùng c a nủ ố ự ế ữ ố ậ ủ 2 + n ch có thỉ ể
là 0 ; 2 ; 6 => n2 + n + 1 ch có th t n cùng là 1 ; 3 ; 7 => nỉ ể ậ 2 + n + 1 không chia h t cho 5. ế
V y không t n t i s t nhiên n sao cho nậ ồ ạ ố ự 2 + n + 1 chia h t cho 1995ế2000.
GV : NguyÔn Thanh H¶i - Trêng THCS Lª §×nh Kiªn 5