CH NG I. Đ I C NG V XÁC SU TƯƠ Ạ ƯƠ Ề Ấ
§1:Bi n c và quan h gi a các bi n cế ố ệ ữ ế ố
1. Phép th và bi n c .ử ế ố
2. Phân lo i bi n cạ ế ố : g m 3 lo iồ ạ
-Bi n c ch c ch n:ế ố ắ ắ
-Bi n c không th có hay không th x y ra:ế ố ể ể ả
-Bi n c ng u nhiên: A, B, C… ế ố ẫ
3. So sánh các bi n cế ố.
Đ nh nghĩa 1.1:ị (A n m trong B hay A kéo theo B) n u ằ ế
A x y ra thì B x y ra.Vâyả ả
Ω
∅
A B
⊂
⇔
A B
A B B A
⊂
= ⇔⊂
Khoa Khoa H c và Máy Tính ọ1Xác Su t Th ng Kê. Ch ng 1 ấ ố ươ
@Copyright 2010
Đ nh nghĩa 1.2:ị A đ c goi la bi n c s c p ươ ế ố ơ ấ
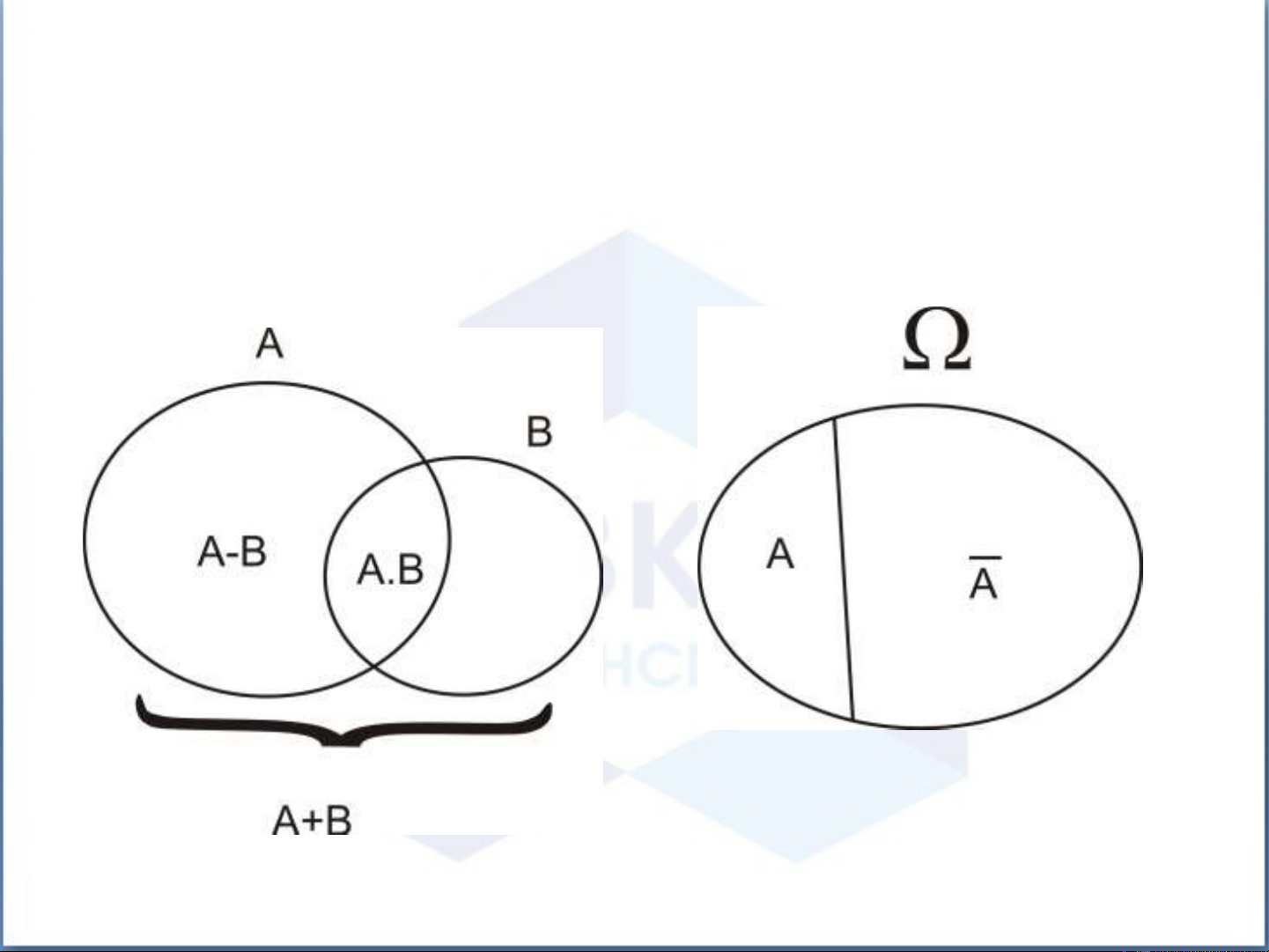
4. Các phép toán trên bi n c (hình 1.1 và 1.2 ):ế ố
x y ra khi và ch khi A x y ra ả ỉ ả và B x y ra.ả
x y ra khi và ch khi A x y ra ả ỉ ả ho cặ B x y ra.ả
x y ra khi và ch khi A x y ra và B không x y ra.ả ỉ ả ả
x y ra khi và ch khi A không x y ra.ả ỉ ả
A B A B+ = ∪
, .B A B A
⇔ ∃ ⊂ ≠
.A B A B= ∩
A B
−
A A= Ω −
Khoa Khoa H c và Máy Tính ọ2Xác Su t Th ng Kê. Ch ng 1 ấ ố ươ
@Copyright 2010
Khoa Khoa H c và Máy Tính ọXác Su t Th ng Kê. Ch ng 1ấ ố ươ
@Copyright 2010
3
•Hình 1.1 Hình 1.2
Khoa Khoa H c và Máy Tính ọXác Su t Th ng Kê. Ch ng 1ấ ố ươ
@Copyright 2010
4
•Các phép toán c a bi n c có tính ch t gi ng các phép toán ủ ế ố ấ ố
c a t p h p, trong đó có các tính ch t đ i ng u:ủ ậ ợ ấ ố ẫ
Ngôn ng bi u di nữ ể ễ : t ng = có ít nh t m t ;tích = t t c đ u.ổ ấ ộ ấ ả ề
(A = có ít nh t 1 ph n t có tính ch t x) suy ra (không A = t t ấ ầ ử ấ ấ
c đ u không có tính ch t x).ả ề ấ
Ví d 1.1:ụ (A = có ít nh t 1 ng i không b lùn) suy ra( không A ấ ườ ị
= t t c đ u lùn).ấ ả ề
Đ nh nghĩa 1.3:ị bi n c A và B đ c g i là xung kh c v i nhau ế ố ượ ọ ắ ớ
n u ế
,
i i i i
i i
i i
A A A A= =
∑ ∑
∏ ∏
.A B = ∅
§2: Các đ nh nghĩa xác su t.ị ấ
•1. Đ nh nghĩa c đi n v xác su tị ổ ể ề ấ
•Đ nh nghĩa 2.1ị: gi s trong m i phép th các k t c c là ả ử ỗ ử ế ụ
đ ng kh năng và có t t c n k t c c nh v y. Kí hi u m là ồ ả ấ ả ế ụ ư ậ ệ
s các k t c c thu n l i cho bi n c A. Khi ây xác su t c a ố ế ụ ậ ợ ế ố ấ ủ
bi n c A là:ế ố
•Ví d 2.1ụ: Trong 1 h p co 6 bi tr ng, 4 bi đen.L y ng u nhiên ộ ắ ấ ẫ
ra 5 bi. Tính xác su t đ l y đ c đúng 3 bi tr ng.ấ ể ấ ươ ắ
•Gi i ả( phân ph i siêu b i)ố ộ
( ) m
An
Ρ =
3 2
6 4
5
10
.C C
C
Ρ=
Khoa Khoa H c và Máy Tính ọ5Xác Su t Th ng Kê. Ch ng 1 ấ ố ươ
@Copyright 2010