
[SAMI-HUST]Viện Toán ứng dụng và Tin học, ĐHBK Hà Nội
Chương 1: Sự kiện ngẫu nhiên và phép tính xác
suất
Trần Minh Toàn (1)
Hà Nội, tháng 8 năm 2012
(1)Email: toantm24@gmail.com
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 1 / 52
Giải tích kết hợp Quy tắc nhân
1.1 Quy tắc nhân
Quy tắc nhân
Nếu có mcách chọn đối tượng x, và sau đó ứng với mỗi cách chọn xnhư thế có ncách
chọn đối tượng y, khi đó có m×ncách chọn đối tượng "xvà y".
Tổng quát: Nếu có m1cách chọn đối tượng x1, với mỗi cách chọn đối tượng x1ta có
m2cách chọn đối tượng x2, . . . , với mỗi cách chọn x1, x2,...,xn−1như thế có mn
cách chọn xn. Khi đó có m1×m2× · · · × mncách chọn đối tượng “x1, x2, . . . và xn”.
Chú ý 1.1
Có thể phát biểu quy tắc nhân theo cách sau: Một công việc được chia làm ngiai đoạn:
giai đoạn thứ nhất có m1cách giải quyết,
giai đoạn thứ 2 có m2cách giải quyết,
. . .
giai đoạn thứ ncó mncách giải quyết.
Khi đó có m1×m2. . . ×mncách giải quyết công việc trên.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 3 / 52
Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Chỉnh hợp lặp
Bài toán
Ta có một tập hợp gồm nphần tử, từ nphần tử này ta sẽ chọn ra kphần tử. Tuỳ vào
điều kiện chọn các phần tử như thế nào (có thứ tự, có lặp) thì số cách chọn kphần tử
cũng có sự khác nhau.
Định nghĩa 1.1
Chỉnh hợp lặp chập kcủa nphần tử là một nhóm có thứ tự gồm kphần tử chọn từ n
phần tử đã cho, trong đó mỗi phần tử có thể được chọn nhiều lần. Ký hiệu số chỉnh hợp
lặp chập kcủa nphần tử bởi ˜
Ak
n.
Công thức tính
˜
Ak
n=nk.(1.1)
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 4 / 52
Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Chỉnh hợp lặp
Ví dụ 1
Xếp 5 cuốn sách vào 3 ngăn. Hỏi có bao nhiêu cách xếp?
Giải:
Mỗi lần xếp một cuốn sách lên là tương đương với việc chọn một trong 3ngăn để cho
sách vào. Mỗi ngăn có thể được chọn nhiều lần. Do đó số cách xếp 5cuốn sách vào 3
ngăn là một chỉnh hợp lặp chập 5của 3phần tử. Vậy số cách xếp là: ˜
A5
3= 35= 243.
Ví dụ 2
Từ 5chữ số 1,2,3,4,5lập được bao nhiêu số có 3chữ số?
Giải:
Mỗi số được lập nên là một cách lấy 3chữ số có thứ tự và có thể giống nhau từ 5chữ
số đã cho. Do đó số các số có 3chữ số được lập nên là: ˜
A3
5= 53= 125.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 5 / 52

Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Chỉnh hợp
Định nghĩa 1.2
Chỉnh hợp chập kcủa nphần tử là một nhóm gồm kphần tử có thứ tự và khác nhau
chọn từ nphần tử đã cho (điều kiện: k≤n). Ký hiệu số chỉnh hợp chập kcủa nphần
tử bởi Ak
n.
Công thức tính
Ak
n=n(n−1) . . . (n−k+ 1) = n!
(n−k)! .(1.2)
Ví dụ 3
Một buổi họp gồm 10 người tham dự, hỏi có mấy cách chọn 1 chủ toạ và 1 thư ký?
Giải:
Ta thấy 2người được chọn làm chủ toạ và thư ký là một cặp (A, B)có thứ tự và khác
nhau được chọn từ 10 người dự họp. Do đó số cách chọn là A2
10 = 10.9 = 90 (cách).
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 6 / 52
Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Hoán vị
Định nghĩa 1.3
Hoán vị của n phần tử là một nhóm có thứ tự có nphần tử gồm đủ mặt nphần tử đã
cho. Ký hiệu số hoán vị của nphần tử bởi Pn.
Chú ý 1.2
Hoán vị là một trường hợp đặc biệt của chỉnh hợp khi k=n(Pn=An
n).
Công thức tính
Pn=n!.(1.3)
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 7 / 52
Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Tổ hợp
Định nghĩa 1.4
Tổ hợp chập kcủa nphần tử (k≤n)là một nhóm không phân biệt thứ tự gồm kphần
tử khác nhau chọn từ nphần tử đã cho. Ký hiệu số tổ hợp chập kcủa nphần tử là Ck
n
Công thức tính
Ck
n=Ak
n
k!=n!
k!(n−k)! =n(n−1) . . . (n−k+ 1)
k!.(1.4)
Chú ý 1.3
Qui ước 0! = 1;
Ck
n=Cn−k
n;
Ck
n=Ck−1
n−1+Ck
n−1.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 8 / 52
Giải tích kết hợp Giải tích kết hợp
Giải tích kết hợp
Tổ hợp
Ví dụ 4
Mỗi đề thi gồm 3câu hỏi lấy trong 25 câu hỏi cho trước. Hỏi có thể lập được bao nhiêu
đề thi có nội dung khác nhau?
Giải:
Số đề thi có thể lập nên là: C3
25 =25.24.23
3! = 2300.
Ví dụ 5
Khai triển nhị thức Newton
(a+b)n=
n
X
k=0
Ck
nan−kbk=C0
nan+C1
nan−1b+· · · +Cn−1
nabn−1+Cn
nbn,
trong đó a, b ∈Rvà n∈N.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 9 / 52

Sự kiện và các phép toán Phép thử và sự kiện
Phép thử và sự kiện
Muốn biết đồng xu ra mặt nào thì tung đồng xu lên, hành động tung đồng xu là
một phép thử.
Muốn biết bắn như thế nào thì phải thực hiện bắn vào bia, hành động bắn súng
vào bia là một phép thử.
. . .
Định nghĩa 2.1
Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó được
gọi là một phép thử. Các kết quả có thể xảy ra của phép thử gọi là sự kiện.
Ví dụ 6
Gieo một con xúc xắc để quan sát số chấm xuất hiện (đây là một phép thử). Các kết
quả sau đều là các sự kiện:
“Xuất hiện mặt kchấm ”, k= 0,1, .., 6
“Xuất hiện mặt chẵn”
“Xuất hiện mặt có số chấm không vượt quá 2”
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 11 / 52
Sự kiện và các phép toán Phép thử và sự kiện
Phép thử và sự kiện
Như vậy sự kiện chỉ có thể xảy ra nếu ta thực hiện phép thử.
Sự kiện sơ cấp: Là sự kiện không thể phân tích được nữa
Sự kiện chắc chắn: Là sự kiện luôn xảy ra trong phép thử, ký hiệu là Ω
Sự kiện không thể: Là sự kiện không bao giờ xảy ra khi thực hiện phép thử. Ký hiệu là
∅.
Sự kiện ngẫu nhiên: Là sự kiện có thể xảy ra cũng có thể không xảy ra khi thực hiện
phép thử.
Phép thử ngẫu nhiên: Phép thử mà các kết quả của nó là các sự kiện ngẫu nhiên.
Để thuận tiện, các sự kiện thường được ký hiệu bằng chữ in hoa: A, B, C, . . .
Ví dụ 7
Gieo một con xúc xắc, khi đó
Ω= “Gieo được mặt có số chấm ≤6và ≥1” là sự kiện chắc chắn;
∅= “Gieo được mặt 7chấm” là sự kiện không thể;
A= “Gieo được mặt chẵn” là sự kiện ngẫu nhiên.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 12 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
Giả sử Avà Blà hai sự kiện trong cùng một phép thử.
Quan hệ kéo theo
Sự kiện Ađược gọi là kéo theo sự kiện B, ký hiệu A⊂B(hoặc A⇒B), nếu Axảy ra
thì Bxảy ra.
Quan hệ tương đương
Hai sự kiện Avà Bđược gọi là tương đương với nhau nếu A⊂Bvà B⊂Avà ký hiệu
là A=B.
Sự kiện tổng
Sự kiện Cđược gọi là tổng của 2sự kiện Avà B, ký hiệu là C=A+B, nếu Cxảy ra
khi và chỉ khi ít nhất một trong 2sự kiện Avà Bxảy ra.
Ví dụ 8
Hai người thợ săn cùng bắn một con thú. Nếu gọi Alà sự kiện người thứ nhất bắn trúng
con thú và Blà sự kiện người thứ 2 bắn trúng con thú, khi đó C=A+Blà sự kiện
con thú bị bắn trúng.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 13 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
Chú ý 2.1
A1+A2+· · · +Anlà sự kiện xảy ra khi có ít nhất một trong nsự kiện đó xảy ra
Mọi sự kiện ngẫu nhiên đều có thể biểu diễn dưới dạng tổng của một số sự kiện sơ
cấp nào đó.
Sự kiện chắc chắn Ωlà tổng của mọi sự kiện sơ cấp có thể. Do đó Ωcòn được gọi
là không gian các sự kiện sơ cấp.
Ví dụ 9
Tung một con xúc xắc. Ta có 6sự kiện sơ cấp Ai(i= 1,6), trong đó Ailà sự kiện xuất
hiện mặt ichấm i= 1,2,...,6.
A= “Xuất hiện mặt có số chấm chẵn”, ta suy ra A=A2+A4+A6
B= “Xuất hiện mặt có số chấm không vượt quá 3”, ta suy ra B=A1+A2+A3.
Khi đó C=A+B=A1+A2+A3+A4+A6.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 14 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
Sự kiện tích
Sự kiện Cđược gọi là tích của 2 sự kiện Avà B, ký hiệu C=A.B (hoặc AB),
nếu Cxảy ra khi và chỉ khi cả Avà Bcùng xảy ra.
Tích của nsự kiện A1.A2. . . Anlà sự kiện xảy ra khi cả nsự kiện cùng xảy ra.
Ví dụ 10
Hai người thợ săn cùng bắn một con thú. Nếu gọi Alà sự kiện người thứ nhất bắn trượt
con thú và Blà sự kiện người thứ 2bắn trượt con thú, khi đó C=A.B là sự kiện con
thú không bị bắn trúng.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 15 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
Sự kiện đối lập
Sự kiện đối lập với sự kiện A, ký hiệu là A, là sự kiện xảy ra khi Akhông xảy ra. Ta có
Ví dụ 11
Gieo một con xúc xắc một lần, khi đó
A= “Gieo được mặt chẵn” suy ra A= “Gieo được mặt lẻ”
A= “Gieo được mặt 1 chấm” suy ra A= “Gieo không được mặt 1 chấm”
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 16 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
Sự kiện hiệu
Hiệu của 2 sự kiện Avà B, ký hiệu là A−B, là sự kiện xảy ra khi và chỉ khi Axảy ra
nhưng Bkhông xảy ra. Thông thường người ta ít sử dụng sự kiện hiệu, mà thường biến
đổi nó thành sự kiện tích như sau: A−B=A.B.
Hai sự kiện xung khắc
Hai sự kiện Avà Bđược gọi là xung khắc với nhau nếu chúng không đồng thời xảy ra
trong một phép thử. Avà Bxung khắc khi và chỉ khi A.B =∅.
Ví dụ 12
Một xạ thủ bắn 1 viên đạn vào bia. Gọi Alà sự kiện xạ thủ đó bắn trúng vòng 8và Blà
sự kiện xạ thủ đó bắn trúng vòng 10. Khi đó ta thấy ngay AB =∅tức là A, B là 2 sự
kiện xung khắc với nhau.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 17 / 52
Sự kiện và các phép toán Quan hệ và phép toán của các sự kiện
Quan hệ và phép toán của các sự kiện
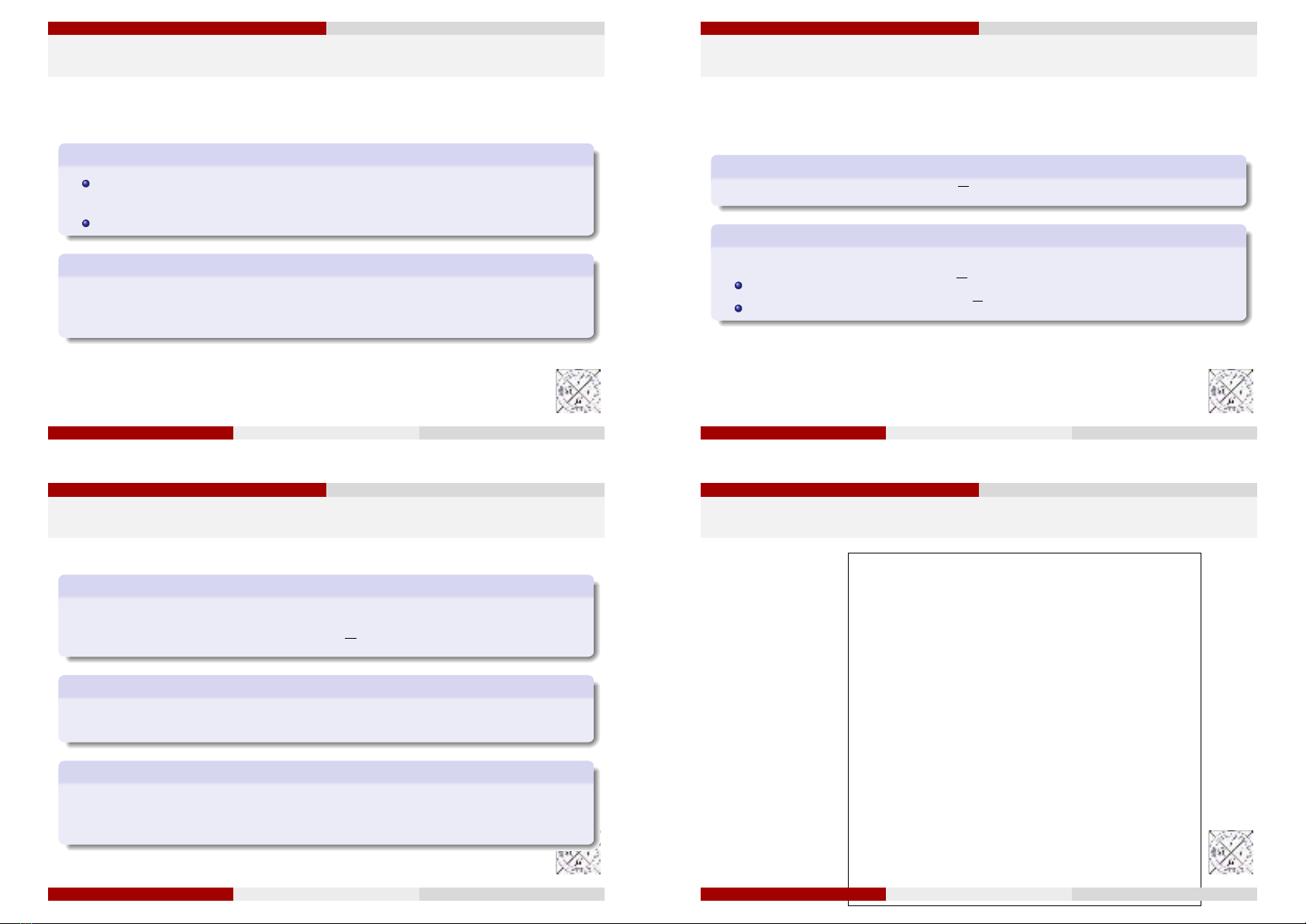
Picture1.png
Hình 1: Sơ đồ Venn thể hiện các phép toán sự kiện
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 18 / 52
Các định nghĩa xác suất Xác suất của một sự kiện
Xác suất của một sự kiện
Định nghĩa 3.1
Xác suất của một sự kiện là một số nằm giữa 0và 1, số này đo lường khả năng xuất hiện
của sự kiện đó khi phép thử được thực hiện. Ký hiệu xác suất của sự kiện Alà P(A).
Một số tính chất cơ bản
0≤P(A)≤1;
P(Ω) = 1; P(∅) = 0;
P(A) + PA= 1.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 20 / 52
Các định nghĩa xác suất Định nghĩa xác suất theo cổ điển
Định nghĩa xác suất theo cổ điển
Định nghĩa 3.2
Xét một phép thử có hữu hạn kết quả có thể xảy ra (có nkết quả), đồng thời các kết
quả này là đồng khả năng xuất hiện; trong đó có mkết quả thuận lợi cho sự kiện A.
Khi đó:
P(A) = m
n=Số trường hợp thuận lợi cho A
Số trường hợp có thể xảy ra .(3.1)
Ví dụ 13
Một người gọi điện thoại nhưng lại quên 2chữ số cuối của số điện thoại cần gọi mà chỉ
nhớ là 2chữ số đó khác nhau. Tìm xác suất để người đó chọn ngẫu nhiên 1số để gọi thì
trúng số cần gọi.
Giải:
Gọi A= “Người đó chọn ngẫu nhiên 1 số gọi thì trúng số cần gọi”.
Số các kết quả có thể xảy ra khi chọn 2chữ số cuối là: n=A2
10 = 90;
Số kết quả thuận lợi cho việc chọn được đúng số cần gọi là m= 1;
Vậy P(A) = m
n=1
90 .
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 21 / 52
Các định nghĩa xác suất Định nghĩa xác suất theo cổ điển
Định nghĩa xác suất theo cổ điển
Ví dụ 14
Trong hộp có 4viên bi trắng và 6viên bi đỏ cùng kích cỡ. Lấy ngẫu nhiên đồng thời ra
2viên bi. Tính xác suất xảy ra sự kiện:
1A= “Được 2 viên bi trắng”;
2B= “Được ít nhất 1 viên bi đỏ”.
Giải:
Số cách lấy ra 2bi từ hộp là n=C2
10 = 45.
1Số cách lấy được 2bi trắng là C2
4= 6. Vậy P(A) = 6
45 =2
15 .
2Ta có B="không có bi đỏ nào", suy ra B=A. Do đó
P(B) = 1 −P(B) = 1 −P(A) = 1 −2
15 =13
15 .
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 22 / 52
Các định nghĩa xác suất Định nghĩa xác suất theo quan điểm hình học
Định nghĩa xác suất theo quan điểm hình học
Định nghĩa 3.3
Giả sử tập hợp vô hạn các kết quả đồng khả năng của một phép thử có thể biểu thị bởi
một miền hình học Ωcó độ đo (độ dài, diện tích, thể tích, . . . ) hữu hạn khác 0, còn tập
các kết quả thuận lợi cho sự kiện Alà một miền A. Khi đó xác suất của sự kiện Ađược
xác định bởi:
P(A) = Độ đo của miền A
Độ đo của miền Ω.(3.2)
Khái niệm đồng khả năng trên Ωcó nghĩa là điểm gieo có thể rơi vào bất kỳ điểm nào
của Ωvà xác suất để nó rơi vào một miền con nào đó của Ωtỉ lệ với độ đo của miền ấy.
Trần Minh Toàn () Xác suất thống kê Hà Nội, tháng 8 năm 2012 23 / 52

























![Quyển ghi Xác suất và Thống kê [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251030/anh26012006/135x160/68811762164229.jpg)
