CHÖÔNG 3
PHEÙP TÍNH VI PHAÂN CUÛA HAØM SOÁ
§3.1. KHAÙI NIEÄM ÑAÏO HAØM VAØ VI PHAÂN
1. ÑAÏO HAØM
Cho haøm soá
:fD
vaø x laø ñieåm trong cuûa D, nghóa laø coù
laân caän
( , )V x x
cuûa x chöùa trong D. Neáu tæ soá
( ) ( )f s f x
sx
coù giôùi haïn khi
sx
thì giaù trò cuûa giôùi haïn naøy ñöôïc goïi laø ñaïo
haøm cuûa f taïi x vaø ñöôïc kyù hieäu laø
()fx
, nghóa laø,
0
( ) ( ) ( ) ( )
( ) lim lim .
h
sx
f s f x f x h f x
fx s x h
Ta cuõng hay vieát
( ) ( ) ( ) ( ) ( )f x f x h f x f s f x
vaø
( ) ,x s x x h x
do ñoù
Neáu ñaët
()y f x
thì
()fx
coøn ñöôïc kyù hieäu laø
dy
dx
hoaëc
x
Dy
.
Neáu hai giôùi haïn sau ñaây toàn taïi
12
( ) ( ) ( ) ( )
lim vaø lim
sx sx
f s f x f s f x
kk
s x s x
thì hai giaù trò k1 vaø k2 laàn löôït ñöôïc goïi laø ñaïo haøm beân traùi vaø ñaïo
haøm beân phaûi cuûa f taïi x. Dó nhieân raèng f coù ñaïo haøm taïi x khi vaø chæ
khi f coù ñaïo haøm hai beân taïi x, ñoàng thôøi giaù trò ñaïo haøm hai beân
baèng nhau.
Tröôøng hôïp moïi ñieåm thuoäc D ñeàu laø ñieåm trong cuûa D thì ta
noùi D laø taäp hôïp môû trong , vaø luùc ñoù neáu f coù ñaïo haøm taïi moïi
ñieåm x thuoäc D thì ta coù ñaïo haøm baäc nhaát
:
( ),
fD
x f x
vaø khi haøm soá
f
cuõng coù ñaïo haøm thì ta coù ñaïo haøm baäc hai cuûa f laø
:
( ) ( ) ( ),
fD
x f x f x
luùc ñoù
()fx
cuõng ñöôïc vieát laø
2
2
dy
dx
hoaëc
2
x
Dy
(neáu ñaët
()y f x
).
Sv caàn döï caùc giôø giaûng & thöïc haønh treân lôùp ñeå hieåu toùm taét noäi dung
2
Toång quaùt, ta coù ñònh nghóa ñaïo haøm baäc n cuûa f theo kieåu qui naïp
1
( 1) ( ) 1
1
( ) ( ) ( ) hoaëc hoaëc ( ).
nn
n n n n
x x x
nn
d y d d y
f x f x D y D D y
dx
dx dx
2. YÙ NGHÓA ÑAÏO HAØM & ÑÒNH NGHÓA SÖÏ KHAÛ VI
Giaû söû haøm soá
:fD
coù ñaïo haøm taïi x.
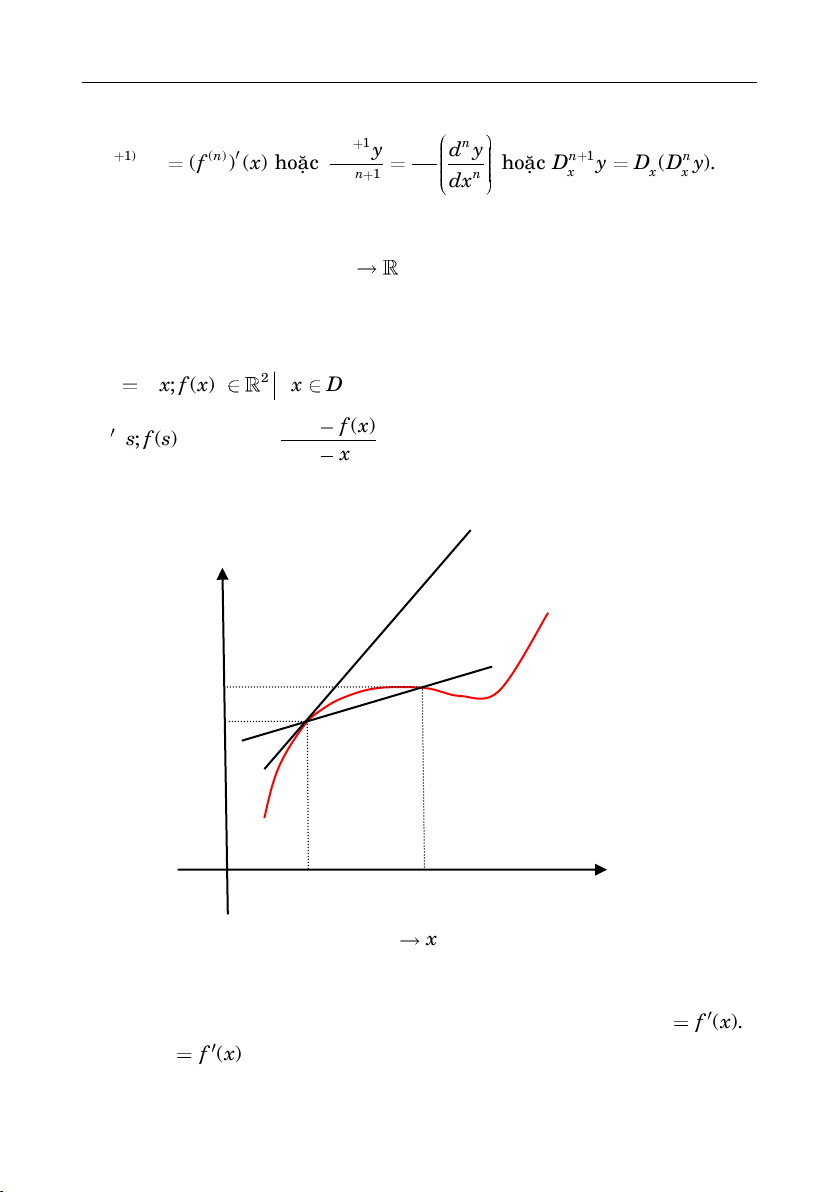
a) Khaùi nieäm tieáp tuyeán
Goïi (C) laø ñoà thò cuûa haøm soá f, nghóa laø
2
( ) ; ( )C x f x x D
. Xeùt caùc ñieåm thuoäc (C) laø
; ( )M x f x
vaø
; ( )M s f s
thì tæ soá
( ) ( )f s f x
sx
laø heä soá goùc caùt tuyeán MM’ cuûa ñöôøng
cong (C), töùc laø giaù trò tan cuûa goùc löôïng giaùc hôïp bôûi tia Ox vôùi tia
MM’:
Theo ñònh nghóa ñaïo haøm, khi
sx
thì M’ tieán veà M treân (C), heä soá
goùc cuûa caùt tuyeán MM’ tieán veà moät giaù trò giôùi haïn k, cuõng coù nghóa
laø caùt tuyeán MM’ di chuyeån ñeán moät vò trí giôùi haïn Mt maø ta goïi laø
tieáp tuyeán taïi M cuûa (C). Heä soá goùc cuûa tieáp tuyeán chính laø
( ).k f x
Giaù trò
()k f x
cuõng noùi leân ñoä doác cuûa (C) taïi M, hoaëc ñoä bieán
f(s)
f(x)
M’
M
t
x
s
x
O
y
Daøn baøi toùm taét noäi dung moân Giaûi Tích Haøm Moät Bieán
3
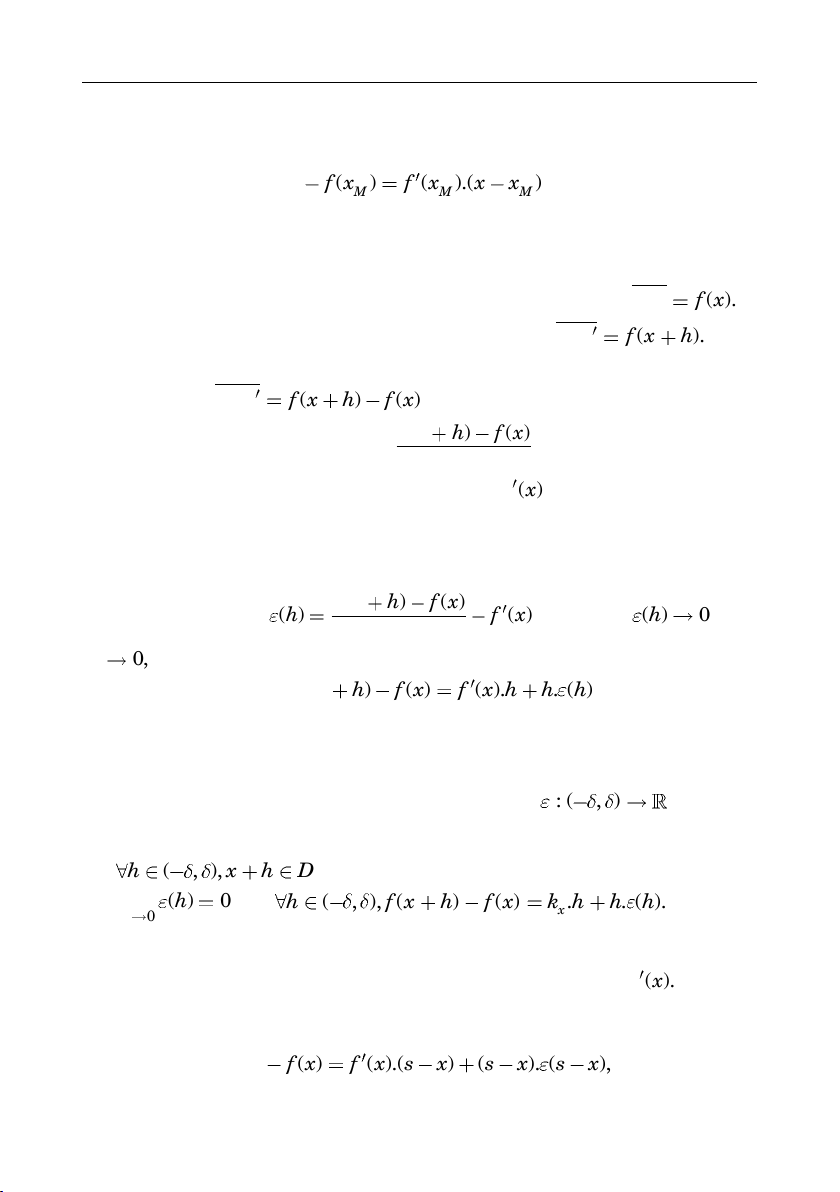
thieân cuûa haøm soá f taïi x. Do ñoù, tieáp tuyeán Mt cuûa (C) taïi ñieåm
; ( )
MM
M x f x
coù phöông trình laø
( ) : ( ) ( ).( )
M M M
Mt y f x f x x x
.
b) Khaùi nieäm vaän toác töùc thôøi
Trong cô hoïc, giaû söû moät ñoäng töû chuyeån ñoäng thaúng treân truïc
x’Ox sao cho taïi thôøi ñieåm x, ñoäng töû ôû vò trí M ñònh bôûi
( ).OM f x
Taïi thôøi ñieåm x + h, ñoäng töû ôû vò trí M’ ñònh bôûi
( ).OM f x h
Vaäy
trong khoaûng thôøi gian h, ñoäng töû di chuyeån ñöôïc quaõng ñöôøng coù ñoä
daøi ñaïi soá laø
( ) ( )MM f x h f x
vaø vaän toác trung bình cuûa ñoäng
töû trong khoaûng thôøi gian ñoù laø
( ) ( )f x h f x
h
. Khi h tieán veà 0, vaän
toác trung bình tieán veà moät giaù trò giôùi haïn
()fx
maø ta goïi laø vaän toác
töùc thôøi cuûa ñoäng töû taïi thôøi ñieåm x.
c) Khaùi nieäm khaû vi vaø vi phaân
Neáu ta ñaët
( ) ( )
( ) ( )
f x h f x
h f x
h
thì ta coù
( ) 0h
khi
0,h
ñoàng thôøi
( ) ( ) ( ). . ( )f x h f x f x h h h
(1)
Töø ñaúng thöùc (1), ta coù khaùi nieäm khaû vi sau ñaây
Ñònh nghóa. Haøm soá f ñöôïc goïi laø khaû vi taïi x, vôùi x laø ñieåm trong
cuûa taäp xaùc ñònh D, coù nghóa laø toàn taïi haøm soá
: ( , )
vaø moät
soá thöïc kx thoûa hai ñieàu sau:
(i)
( , ),h x h D
(ii)
0
lim ( ) 0
hh
vaø
( , ), ( ) ( ) . . ( ).
x
h f x h f x k h h h
Deã thaáy raèng f khaû vi taïi x töông ñöông vôùi f coù ñaïo haøm taïi
x. Hôn nöõa, khi f khaû vi taïi x thì soá kx trong (ii) cuõng laø
( ).fx
Ñaúng thöùc (1) coù theå ñöôïc vieát laïi döôùi daïng
( ) ( ) ( ).( ) ( ). ( ),f s f x f x s x s x s x
Sv caàn döï caùc giôø giaûng & thöïc haønh treân lôùp ñeå hieåu toùm taét noäi dung
4
trong ñoù
( ) 0sx
khi
.sx
Neáu kyù hieäu
,x s x
ñöôïc goïi laø
soá gia cuûa x, vaø kyù hieäu
( ) ( ),y f s f x
ñöôïc goïi laø soá gia cuûa
()y f x
thì ñaúng thöùc treân ñöôïc vieát laïi nhö sau
( ). . ( ).y f x x x x
Khi soá gia x “raát laø nhoû” thì ta thaáy
( ). ,y f x x
vaø yù
nghóa cuûa söï xaáp xæ naøy ñöôïc kyù hieäu bôûi ñaúng thöùc
()dy f x dx
, kyù
hieäu dy ñöôïc goïi laø vi phaân cuûa haøm soá
()y f x
taïi x. Ñaúng thöùc
()dy f x dx
cuõng giaûi thích cho yù nghóa cuûa kyù hieäu
dy
dx
ñeå chæ ñaïo
haøm cuûa
()y f x
taïi ñieåm x, noùi caùch khaùc
0
lim ( ).
x
dy y fx
dx x
Baøi taäp
1. Duøng ñònh nghóa ñaïo haøm, chöùng minh raèng
a) Neáu
2
( ) thì ( ) 2 ;f x x f x x
b) Neáu
32
( ) thì ( ) 3 ;f x x f x x
c) Neáu
1
( ) thì ( ) (vôùi 0);
2
f x x f x x
x
d) Neáu
3
32
1
( ) thì ( ) (vôùi 0).
3
f x x f x x
x
2. Söû duïng ñònh nghóa ñaïo haøm vaø chaáp nhaän keát quaû
0
sin
lim 1,
u
u
u
haõy chöùng minh ñaïo haøm cuûa sin laø cos; ñaïo haøm
cuûa cos laø
sin
.
3. Khaûo saùt ñaïo haøm beân traùi vaø beân phaûi taïi x = 2 cuûa haøm soá f
ñònh bôûi
( ) 2 3.f x x
4. Khaûo saùt ñaïo haøm beân traùi vaø beân phaûi taïi x = 1 cuûa haøm soá f
ñònh bôûi
2
( ) 2 1 .f x x x x
Daøn baøi toùm taét noäi dung moân Giaûi Tích Haøm Moät Bieán
5
5. Khaûo saùt söï khaû vi taïi x = 0 cuûa haøm soá
:f
ñònh bôûi
1
sin khi 0,
()
0 khi 0.
xx
fx x
x
6. Cho haøm soá
:f
ñònh bôûi
21
sin khi 0,
()
0 khi 0.
xx
fx x
x
Chöùng minh f coù ñaïo haøm taïi x = 0 vaø tính
( ).fx
7. Cho haøm soá
:f
ñònh bôûi
31
sin khi 0,
()
0 khi 0.
xx
fx x
x
Chöùng minh f coù ñaïo haøm caáp hai taïi x = 0.