Chuyên đề 3: TỨ GIÁC – HÌNH THANG – HÌNH THANG CÂN

Chia sẻ: Lotus_3 Lotus_3 | Ngày: | Loại File: PDF | Số trang:12

Thêm vào BST

Báo xấu

606
lượt xem 54
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng. A, B, C, D là các đỉnh ; AB, BC, CD, DA là các cạnh. Ta chỉ xét tứ giác đơn trong đó các cạnh chỉ có thể cắt nhau tại các đỉnh. Trong tứ giác đơn ABCD, ta phân biệt : hai đỉnh kề nhau (cùng nằm trên một cạnh ) với hai đỉnh đối nhau(không kề nhau(xuất phat từ một đỉnh) với hai cạnh đối (không kề nhau)....

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chuyên đề 3: TỨ GIÁC – HÌNH THANG – HÌNH THANG CÂN

Chuyên đề 3: TỨ GIÁC – HÌNH THANG – HÌNH THANG CÂN *) Khái niệ m chung về tứ giác: +) Định nghĩa : a) Tứ giác ABCD là hình gồ m bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng. A, B, C, D là các đỉnh ; AB, BC, CD, DA là các cạnh. Ta chỉ xét tứ giác đơn trong đó các cạnh chỉ có thể cắt nhau tại các đỉnh. Trong tứ giác đơn ABCD, ta phân biệt : hai đỉnh kề nhau (cùng nằm trên một cạnh ) với hai đỉnh đối nhau(không kề nhau(xuất phat từ một đỉnh) với hai cạnh đối (không kề nhau). Đường chéo của tứ giác là đoạn thẳng nối hai đỉnh đối nhau. Trong tập hợp , các điểm của mặt phẳng chứa một tứ giác đơn, ta phân biệt điể m thuộc tứ giác, điẻ m trong tứ giác, điểm ngoài tứ giác. b) ABCD là tứ giác lồi  ABCD luôn thuộc nửa mặt phẳng với bờ là đường A thẳng chứa bất kỳ cạnh nào của nó. B Tứ giác (đơn) không lồi là tứ giác lõm. D C Trong hình, ABCD là tứ giác lồi
1. Định lí: Tổng các gọc trong tứ giác bằng 3600 . *) Tìm hiểu sâu về tứ giác giác lồi: Định lí : Trong một tứ giác lồi , hai đường chéo cắt nhau. Đảo lại, nếu một tứ giác có hai đường chéo cắt nhau thì đó là một tứ giác lồi. ABCD lồi  ABCD có hai đường chéo cắt nhau. Để chứng minh định lí, cần nhớ lại mấy định lí sau đây: Tia Oz nằm trong gọc xOy  tia Oz cắt đoạn thẳng MN, với (I) M  Oz, N Oy Néu tia Oz nằ m trong xOy thì Oz và Oy nằm trong nửa mặt (II) phẳng bờ chứa Oy; Oz và O x nằm trong nửa mặt phẳng bờ chứa Oy. 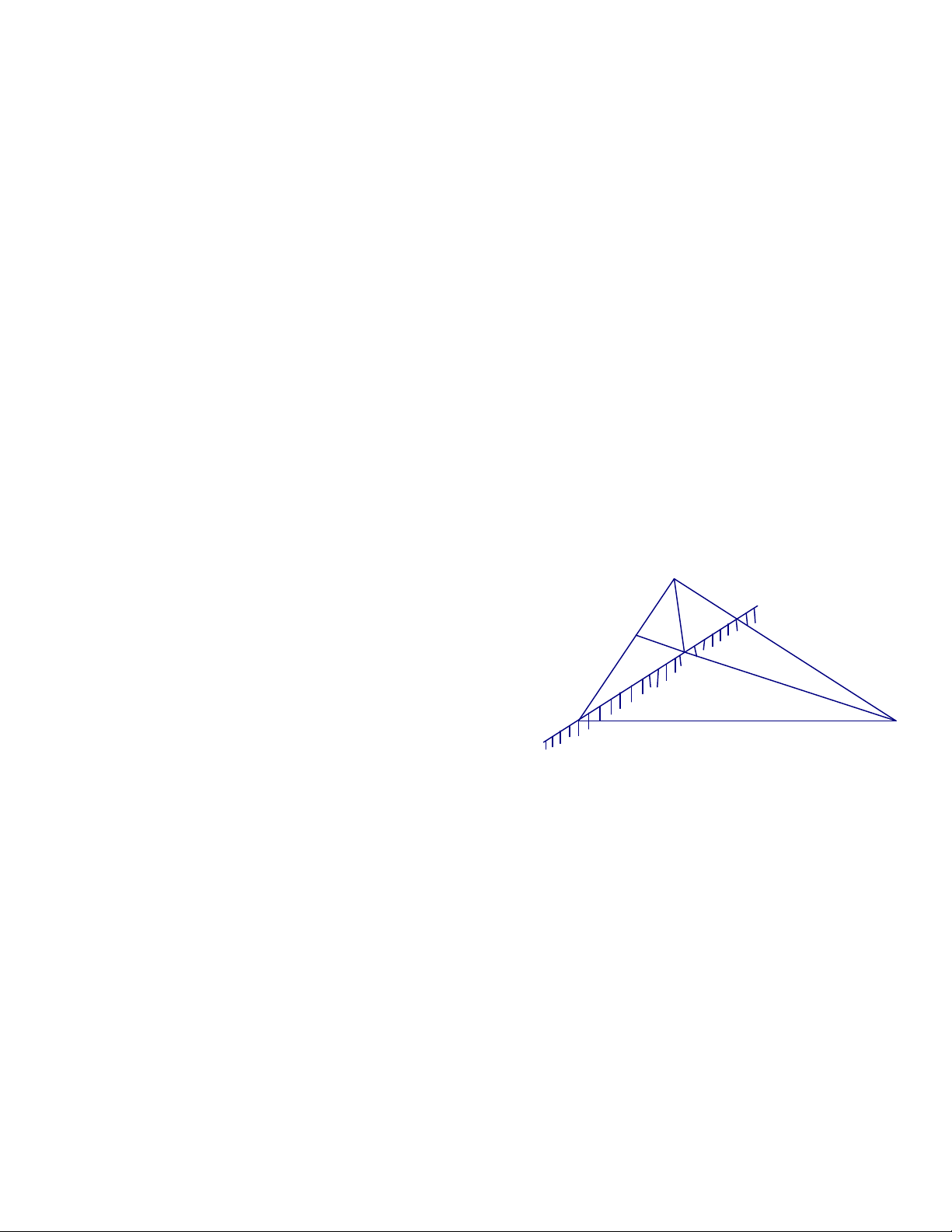(III) Cho tam giác ABC a) Các trung tuyến xuất phát từ các điểm A và C cắt nhau tại điểm M. Tứ giác ABCM là lồi hay không lồi? Vì sao?
b) M là một điểm tuỳ ý thuộc miền trong của tam giác ABC( không thẳng hàng với hai đỉnh nào của tam giác). Với vị trí nào của điểm M thì ABCM là tứ giác lồi? c) M và N là hai điểm tuỳ ý thuộc miền trong của tam giác ABC( và không thẳng hàng với đỉnh nào của tam giác). Chứng minh rằng trong năm điể m A, B, M, N, C bao giờ cũng chọn ra được bốn điểm là đỉnh của một tứ giác lồi. B Giải a) ABCM không lồi (lõm), vì B và C nằm ở hai M nửa mặt phẳng đối nhau có bờ chứa AM (h .2a) A C b) Kết quả ở câu a/ cũng đúng khi M là điểm bất kì thuộc miền trong của tam giác ABC. Nếu M thuộc miền ngoài của ABC thì có hai trường hợp : - M ở trong góc đối đỉnh của một góc của tam giác. trong h .2b, M ở trong góc đối đỉnh của góc B . Dễ thấy rằng lúc đó đỉng B lại là điểm thuộc miền trong của tam giác MAC, do đó AMCB không lồi(lõm).
- M ở trong một góc của tam giác. trong hình 2b, M’ nằm trong góc A. Do đó AM’ là tia trong của góc A, mà A và M’ nằm ở hai phía của cạnh BC, cho nên đoạn Am’ cắt đoạn thẳng BC và ABM’C là tứ giác lồi. Tóm lại, trong h .2b, các miền được gạch chéo là tập hợp các điểm M mà MABC là tứ giác lõm. Các miền khác (để trắng ) là tập hợp các điểm M mà M, A, B, C là các j M đỉnh của tứ giác lồi. B M' A C
c) Đường thẳng đi qua hai điể m M và N bao giờ cũng không cắt một cạnh của tam giác ABC. Trong h .2c, đường thẳng MN không cắt AC. Tứ B giác MNCA là tứ giác lồi(điể m N thuộc miền ngoài M N của tam giác MAC và nằm trong góc MAC). C A H .2a CÁC VÍ DỤ : Ví d ụ 1 : Chứng minh rằng trong một tứ giác lồi tổng độ dài các cạnh(chu vi) lớn hơn tổng độ dài các đường chéo và nhỏ hơn hai lần tổng độ dài các đường chéo. *) Nhận xét : Đây là bài toán về chứng minh bất đẳng thức về các độ dài. nên kẻ thêm các đường phụ, xét các tam giác để áp dụng mệnh đề :” Trong một tam giác, toỏng độ dài hai cạnh lớn hơn độ dài cạnh thứ ba”. Giải B C o D A
Cho tứ giác ABCD(h. 7). Ta phải chứng minh : AC + BD < AB + BC + CD + DA < 2( AC + BD) 1) Chứng minh AC + BD < AB + BC + CD + DA Ta có : (bất đẳng thức trong  ABC) AC < AB +BC AC < AD + DC (bất đẳng thức trong  ADC) BD < BC + CD (bất đẳng thức trong  BCD) BD < BA + AD (bất đẳng thức trong  BAD) Từ đó : 2( AC + BD) < 2(AB +BC + CD + DA) AC + BD < AB + BC + CD + DA 2) Chứng minh AB + BC + CD + DA < 2( AC + BD). Trong tam giác ABO và CDO, ta có : AB < BO + OA (1) CD < CO + OD (2) Cộng (1) và (2) ta có : AB + CD < BO + OD + CO + OA AB + CD < BD + AC (3)
Tương tự, trong tam giác BCO và ADO, ta có : AD + BC < BD + AC (4) Từ (3) và (4) ta được : (đpcm) AB + BC + CD + DA < 2( AC + BD). *) Nhận xét: 1) Từ mỗi bất đẳng thức (3) và (4) ta thấy vế trái là tổng của hai cạnh của tứ giác, còn vế phải là tổng của hai đường chéo. Vậy có thể phát biểu mệnh đề : “ Trong một tứ giác giác lồi, tổng của hai cạnh đối nhỏ hơn tổng của hai đường chéo”. 2) Nếu tứ giác ABCD không lồi, thì hai bất đẳng thức trong bài 7 có còn đúng không ? vì sao? Ví d ụ 2 : Cho một tứ giác lồi ABCD, Tronh đó AB + BD không lớn hơn AC + C CD. B Chứng minh rằng : AB < AC. O D Giải Gọi giao điể m của AC và BD là O A Trong tam giác AOB, ta có :
AB < AO + OB (1) Trong tam giác COD, ta có : CD < CO + OD (2) Từ (1) và (2) ta có : AB + CD < BO + OD + CO + OA AB + CD < AC + BD (3) Theo giả thiết : AB + BD  AC + CD (4) Từ (3) và (4) suy ra AB < AC.(đpcm) Ví d ụ 3 : Cho tứ giác lồi ABCD. Gọi P và Q là trung điểm của hai cạnh AD và BC. Chứng minh rằng : DC  AB PQ  2 Gợ i ý : B ở đây có bất đẳng thức giữa độ dài các đoạn A thẳng , nên kẻ đường phụ để có các hình tam Q P F C D
giác, lại có trung điểm của các cạnh, nên nhgĩ đến việc áp dụng định lí về đường trung bình trong tam giác. Giải Tứ giác ABCD GT PA = PD, QB = QC DC  AB KL PQ  2 CM : Ta kẻ thêm đường chéo AC và lấy trung điểm F của AC. Trong tam giác ACD, PF là đường trung bình, do đó : DC PF = 2 Trong tam giác ACD, PF là đường trung bình. do đó : AB QF = 2 Nếu P,Q và F không thẳng hàng thì trong tam giác PQF ta có: DC  AB PQ < PF + QF = 2 Nếu P, Q, và F thẳng hàng thì F là điểm nằm giữa của hai đoạn thẳng PQ và ta có :
DC  AB PQ = PF + QF = 2 Như vậy trong mọi trường hợp, ta có : DC  AB PQ  . ( đpcm) 2 Nhận xét : Có thể thấy ngay rằng : P, Q, F thẳng hàng AB//CD.  Do đó ta chứng minh được rằng : DC  AB PQ  . 2 Trong đó dấu = xảy ra khi và chỉ khi AB//CD. Như vậy, qua việc giải bài toán trên, ta chứng minh cùng một lúc hai định lí: CD  AB (1) Nếu ABCD là hình thang (AB//CD) thì PQ = 2 (2) Nếu ABCD không là hình thang (AB//CD) thì PQ  CD  AB DC  AB và PQ < 2 2
CÁC BÀI TẬP : Bài tập 1: Cho A, B, C, D là bốn đỉnh của một tứ giác lồi,E là một điể m thuộc miền trong của ttam giác OCD, với O là giao điểm của hai đoạn thẳng AC và BD. Chỉ ra tứ giác lồi nhận bốn trong năm điểm A, B, C, D, E. Bài tập 2: Chứng minh rằng từ năm điểm bất kì trong mặt phẳng(không có ba điểm nào thẳng hàng) Bao giờ cũng chọn được bốn điể m là các đỉnh của một tứ giác lồi. Bài tập 3: Chứng minh rằng trong một tứ giác lồi có các góc không bằng nhau thì có ít nhất một góc tù. Bài tập 4:
Cho tứ giác lồi ABCD, hai cạnh AD và BC kéo dài gặp nhau tại E, hai cạnh AB và CD kéo dài gặp nhau tại M. Kẻ hai phân giác của hai góc CED và BMC cắt nhau tại K. tính góc EKM theo các góc trong của tứ giác ABCD.