Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Ch−¬ng II:
D¢Y RUNG - ph−¬ng tr×nh Dal¨mbE
§1. Dao ®éng ngang cña ®©y - Ph−¬ng tr×nh §al¨mbe:
1) Quan s¸t sù lan truyÒn biÕn d¹ng däc theo d©y:
Mét sîi d©y, mét ®Çu g¾n vµo t−êng, ®Çu kia ®−îc kÐo c¨ng bëi nguêi quan s¸t (H×nh 2). Khi
ng−êi quan s¸t t¹o mét biÕn d¹ng ë ®Çu d©y, biÕn d¹ng nµy sÏ ch¹y däc theo d©y tõ ®iÓm nµy sang
®iÓm kh¸c, t¹o nªn mét sãng lan truyÒn däc theo d©y, t−¬ng tù nh− sãng biÕn d¹ng lan truyÒn
trong chuçi v« h¹n c¸c dao ®éng tö liªn kÕt.
a) Sãng ngang vµ sãng däc:
XÐt mét sãng lan truyÒn trong mét chuçi v« h¹n c¸c dao ®éng tö liªn kÕt vµ mét sãng lan truyÒn
trªn d©y. Hai sãng nµy lan truyÒn theo ph−¬ng Ox (gäi lµ ph−¬ng truyÒn sãng). Tuy nhiªn, vËt
dao ®éng trong chuçi dao ®éng tö chuyÓn ®éng theo ph−¬ng song song víi Ox, cßn dÞch chuyÓn
cña mét ®iÓm trªn d©y theo ph−¬ng vu«ng gãc víi Ox.
Sãng ngang: lµ sãng mµ c¸c phÇn tö cña m«i tr−êng chuyÓn ®éng trong mÆt ph¼ng vu«ng gãc
víi ph−¬ng truyÒn sãng. VÝ dô, sãng trªn d©y ®µn c¨ng th¼ng...
a) Sãng ngang b) Sãng däc
H×nh 1
Ph−¬n
g
tru
y
Òn sãn
g
Ph−¬ng truyÒn sãng
Sãng däc: lµ sãng mµ ph−¬ng dao ®éng cña c¸c phÇn tö cña m«i tr−êng trïng víi ph−¬ng
truyÒn sãng. VÝ dô, sãng ©m trong kh«ng khÝ, sãng biÕn d¹ng truyÒn trong chuçi c¸c dao ®éng tö
liªn kÕt...
b) ChiÒu truyÒn sãng - Sãng ch¹y :
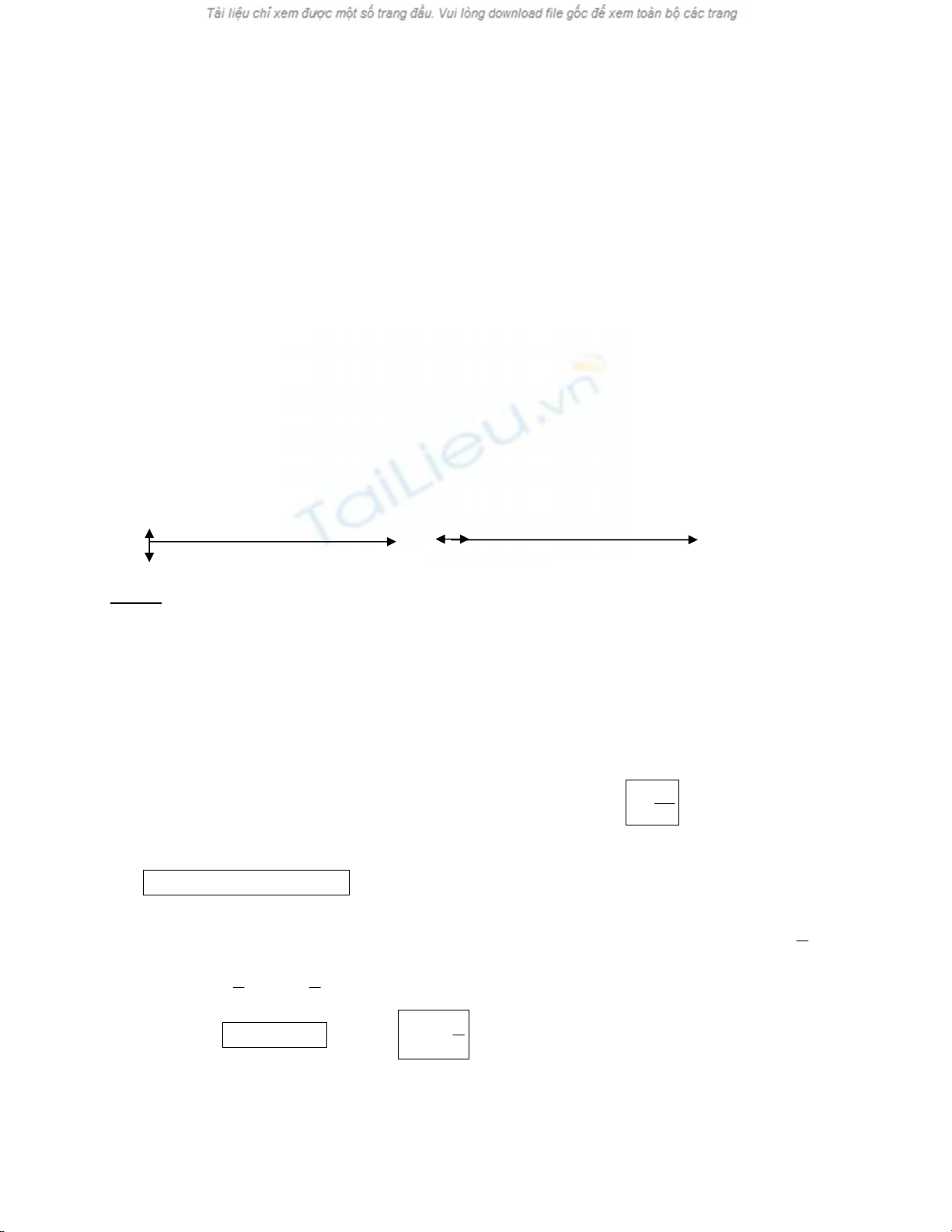
Quan s¸t sù lan truyÒn cña sãng trªn d©y t¹i nh÷ng thêi ®iÓm kÕ tiÕp nhau t0, t1= t0 +∆t, t2 = t0
+2∆t, ..., tn= t0 + n∆t (H×nh 2). Ta thÊy r»ng, biÕn d¹ng cña d©y t¹i c¸c thêi ®iÓm kh¸c nhau lµ nh−
nhau, nh−ng trong kho¶ng thêi gian ∆t, biÕn d¹ng truyÒn ®i ®−îc mét kho¶ng ∆x tØ lÖ víi ∆t:
∆x = c. ∆t ⇒ Sãng biÕn d¹ng ®· lan truyÒn däc theo d©y víi vËn tèc
x
ct
∆
=
∆
kh«ng ®æi theo chiÒu
x t¨ng (c ®−îc gäi lµ vËn tèc truyÒn sãng)
DÞch chuyÓn ψ(x,t) cña d©y t¹i (x + c∆t, t + ∆t) vµ t¹i (x,t) lµ nh− nhau:
(., )(,)
x
ctt t xt
ψ
ψ
+∆ +∆=
Khi sãng trªn d©y lan truyÒn theo ph−¬ng chiÒu Ox, dÞch chuyÓn cña mét ®iÓm M täa ®é x
trªn d©y t¹i thêi ®iÓm t sÏ gièng nh− dÞch chuyÓn cña ®iÓm O (x = 0) t¹i thêi ®iÓm
x
utc
=− ⇒
(,) (0, ) ( )
x
x
xt t f t
cc
ψ
=−=−
⇒ Hµm ψ(x,t) chØ phô thuéc vµo biÕn sè duy nhÊt :
(,) ()
x
tfu
ψ
= (1) víi
x
utc
=
− .
§©y lµ sãng ch¹y theo ph−¬ng Ox theo chiÒu x t¨ng.
46
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
• Ta cã :
22
22
f
f
x
x
xx
ψ
∂
⎛⎞
∂⎜⎟
∂∂ ∂
⎝⎠
==
∂∂ ∂
. Mµ : 1
..
ffuf
x
ux u c
∂∂∂∂
⎛⎞
=
=−
⎜⎟
∂∂∂∂
⎝⎠
⇒
2 2
222
11
..
11 1
ff f
f
cu x cu
x
xcucuc
ψ
∂∂ ∂
⎛⎞⎛⎞⎛⎞
∂− ∂ ∂−
⎜⎟⎜⎟⎜⎟
∂∂
∂∂ ∂
⎝⎠⎝⎠⎝⎠
==−=− =
∂∂ ∂ ∂ u
∂
(a)
MÆt kh¸c:
2
2
f
fu
uu
∂
⎛⎞
∂⎜⎟
∂∂
⎝⎠
=
∂∂
víi .
f
ft f
utut
∂∂∂∂
==
∂∂∂∂
⇒22
22
fff
ff
tut
uu t tt
2
2
t
ψ
∂∂∂
⎛⎞ ⎛⎞ ⎛⎞
∂∂∂
⎜⎟ ⎜⎟ ⎜⎟
∂
∂∂
∂∂ ∂
⎝⎠ ⎝⎠ ⎝⎠
=====
∂
∂∂∂∂∂
(b)
Tõ (a) vµ (b), suy ra : 22
222
1
x
ct
ψ
ψ
∂∂
=
∂
∂ ⇒Hµm sãng (,) ((,))
x
tfuxt
ψ
=
lµ mét nghiÖm cña ph−¬ng
tr×nh truyÒn sãng §al¨mbe.
• TiÕp tôc quan s¸t (H×nh 3) ⇒ BiÕn d¹ng khi ®Õn t−êng, sÏ t¹o nªn mét sãng ph¶n x¹ lan truyÒn
víi vËn tèc c cña sãng tíi, nh−ng theo chiÒu x gi¶m vµ cã d¹ng: (,) (v)
x
tg
ψ
=
víi v
x
tc
=+ .
§©y lµ sãng ch¹y theo ph−¬ng Ox theo chiÒu x gi¶m.
• T−¬ng tù, hµm sãng (,) (v(,))
x
tgxt
ψ
=lµ mét nghiÖm cña ph−¬ng tr×nh truyÒn sãng §al¨mbe.
H×nh 2 H×nh 3
47
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
2) Ph−¬ng tr×nh chuyÓn ®éng cña d©y:
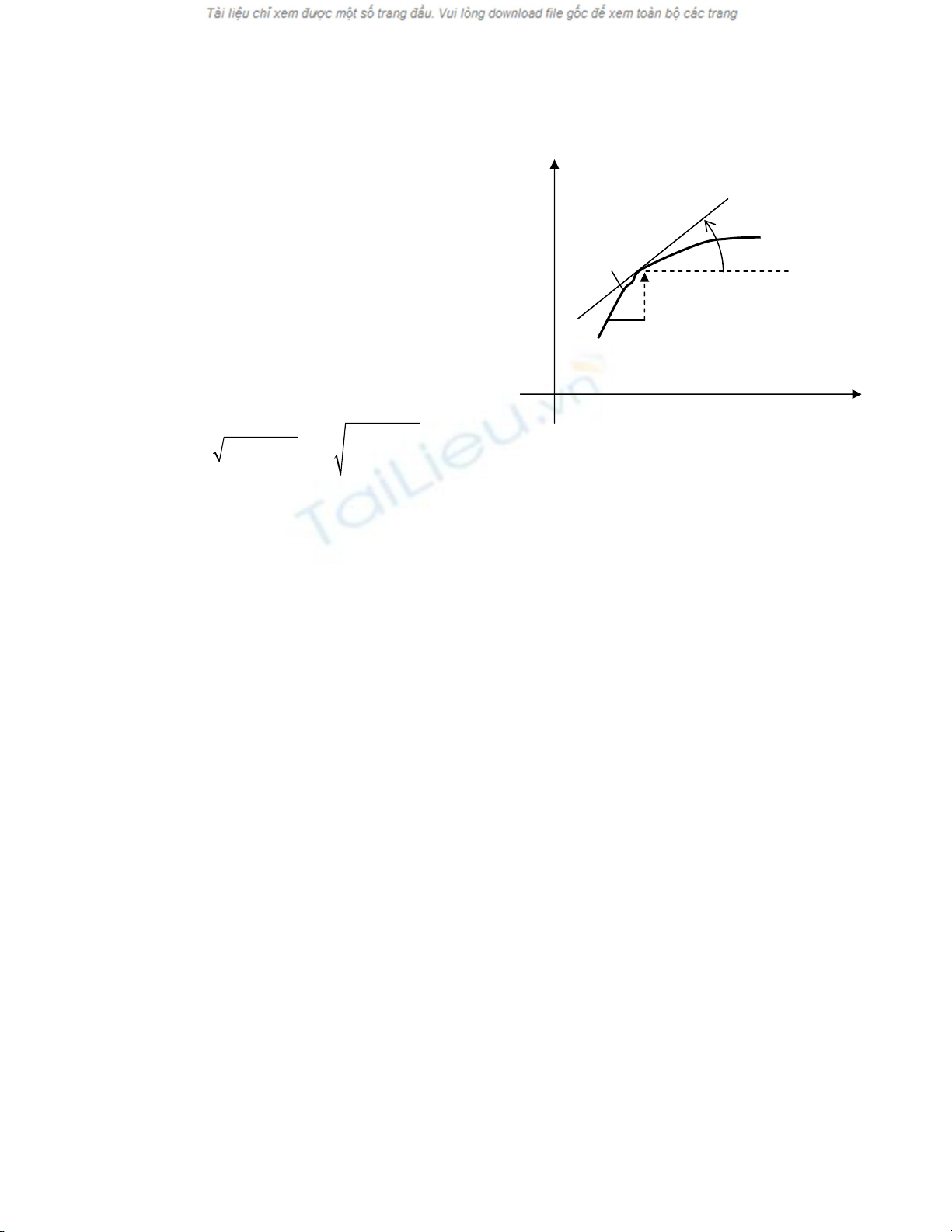
a) M« t¶ c¸c chuyÓn ®éng ngang nhá : y
• XÐt mét sîi d©y c¨ng th¼ng n»m theo ph−¬ng trôc
Ox. Khi gâ lªn d©y, d©y sÏ rung ®éng. §Ó ®¬n gi¶n
chØ xÐt chuyÓn ®éng cña sîi d©y trong mÆt ph¼ng
xOy.
Gäi : ψ(x,t) lµ dÞch chuyÓn theo ph−¬ng Oy cña d©y
t¹i hoµnh ®é x, t¹i thêi ®iÓm t (dÞch chuyÓn ngang);
α(x,t) gãc gi÷a tiÕp tuyÕn víi d©y t¹i hoµnh ®é x, t¹i
thêi ®iÓm t so víi trôc Ox n»m ngang.
D©y rung víi biªn ®é bÐ Cã thÓ xem nh− d©y vÉn
th¼ng Gãc nghiªng α(x,t) cña d©y rÊt bÐ:
⇒
⇒
(,)
(,) (,)
x
x
t
xt tg xt x
ψ
αα
∂
⎡⎤
≈=
⎢⎥
∂
⎣⎦
Hoµnh ®é cong s ®o däc theo d©y cung nghiÖm ®óng
hÖ thøc:
2
22 1d
ds dx d dx dx
dx
ψ
ψ
⎛⎞
=+=+ ≈
⎜⎟
⎝⎠ tøc lµ
hoµnh ®é cong s cã thÓ coi nh− b»ng hoµnh ®é ngang x ChuyÓn ®éng cña mét ®iÓm trªn d©y
theo ph−¬ng Ox n»m ngang cã thÓ bá qua ⇒ Sãng lan truyÒn trªn d©y cã thÓ xem nh− lµ c¸c
sãng ngang.
⇒
M
dx
ds
d
ψ
(,)
x
t
ψ
(,)
x
t
α
H×nh 4
x
O x
b) Lùc c¨ng d©y :
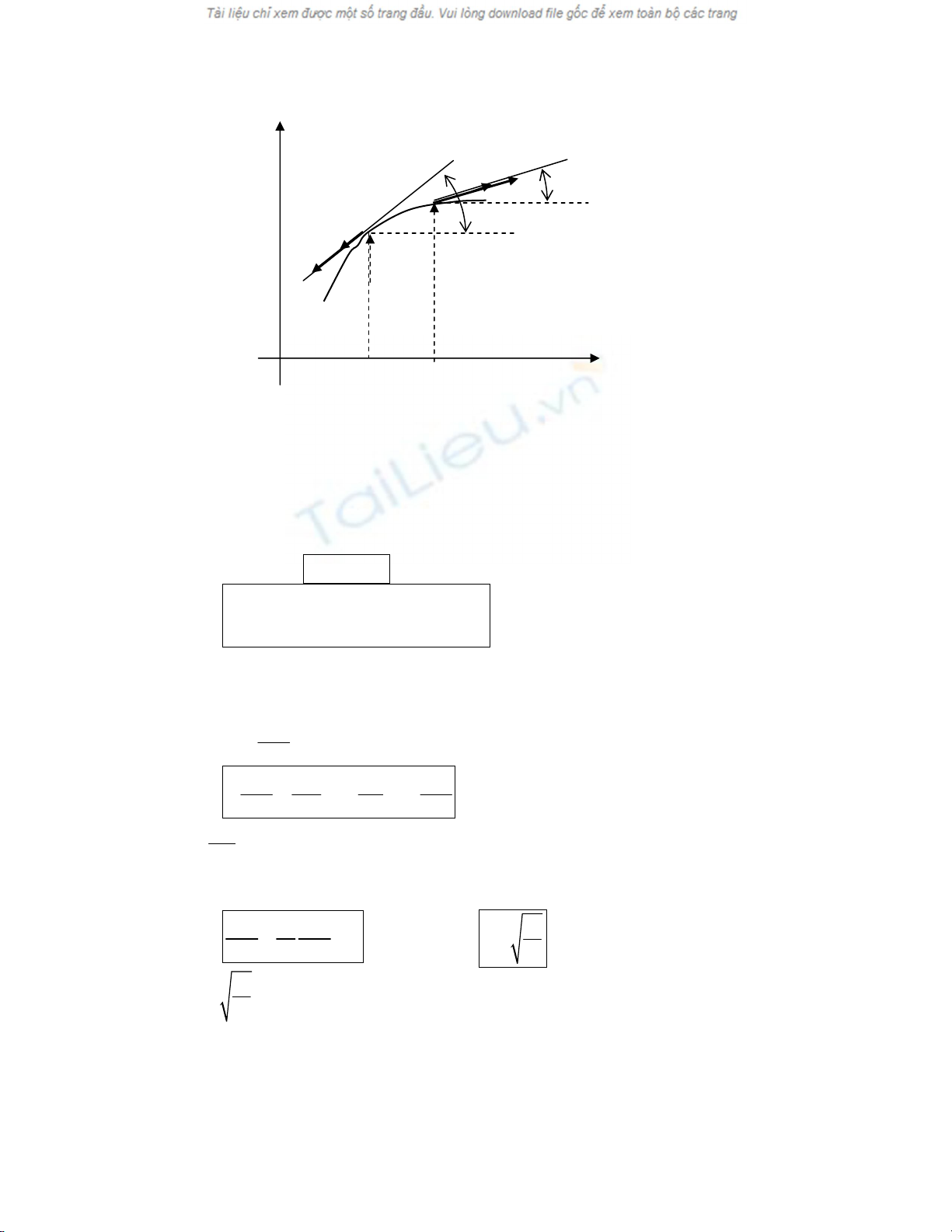
XÐt c¸c lùc t¸c dông lªn ph©n tè d©y cã chiÒu dµi dx, n»m gi÷a x vµ x + dx (H×nh 5).
Gäi T(x,t) lµ gi¸ trÞ lùc c¨ng d©y t¹i mét ®iÓm cã hoµnh ®é x, t¹i thêi ®iÓm t.
Bá qua träng l−îng cña d©y. Gi¶ sö bá qua ®é cøng xo¾n cña d©y ⇒ D©y kh«ng chÞu t¸c dông cña
momen xo¾n; c¸c lùc t¸c dông lªn d©y h−íng theo tiÕp tuyÕn víi d©y.
Gäi (,)
F
xt
: lùc c¨ng t¸c dông t¹i thêi ®iÓm t, tõ phÇn d©y cã täa ®é > x lªn phÇn d©y cã täa ®é
< x. PhÇn d©y cã täa ®é nhá h¬n x t¸c ®éng lªn ph©n tè d©y dx mét lùc:
11
(,) (,)
F
Fxt Txtu=− =
PhÇn d©y cã täa ®é lín h¬n x+dx t¸c ®éng lªn ph©n tè dx mét lùc:
22
(,)(,)FFxdxtTxdxtu=+ + = +
víi vµ lµ vect¬ ®¬n vÞ cña tiÕp tuyÕn víi d©y t¹i x vµ x + dx t¹i thêi ®iÓm t.
1
u
2
u
C¸c thµnh phÇn cña vµ trªn c¸c trôc Ox vµ Oy:
1
F
2
F
Trªn Ox: Trªn Oy :
1
2
(,)
(,
x
x
FTxt
FTxdxt
≈−
⎧
⎨≈+
⎩)
1
2
(,) (,). (,)
( ,) ( ,). ( ,)
yy
yy
FFxtTxtxt
F
Fxdxt Txdxt x dxt
α
α
=− ≈−
⎧
⎪
⎨
=+≈+ +
⎪
⎩
(L−u ý : cosα ≈ 1, sin ≈ α).
48
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
y
O x
x
M
(,)
x
t
ψ
(,)
x
t
α
1
F
1
u
(,)
x
dx t
ψ
+
(,)
x
dx t
α
+
2
F
2
u
x + dx
H×nh 5
¸p dông ®Þnh luËt Newton II cho ph©n tè d©y dx, vµ chiÕu lªn Ox :
(,)(,)Tx dxt Txt+− =0
)
t T=
⇒
(,)(,Tx dxt Txt+=
⇒ T¹i thêi ®iÓm t, lùc c¨ng d©y T b»ng h»ng sè däc theo d©y.
MÆc kh¸c, chiÒu dµi cña d©y xem nh− kh«ng ®æi lùc c¨ng nãi trªn lu«n b»ng lùc c¨ng T⇒0 khi
d©y kh«ng chuyÓn ®éng: Tx 0
(,)
10
20
(,) .(,)
(,).(,)
yy
yy
FFxtTxt
F
Fxdxt T xdxt
α
α
=− =−
⎧
⎪
⎨=+= +
⎪
⎩
Tõ ®ã suy ra: (2)
c) Ph−¬ng tr×nh chuyÓn ®éng ngang :
Gäi µ lµ khèi l−îng mét ®¬n vÞ chiÒu dµi d©y. ¸p dông ®Þnh luËt Newton II cho ph©n tè d©y dx
(khèi l−îng µ .dx) vµ chiÕu lªn Oy:
[]
2
21 0
2(,)(,).
(,)(,
yyy y
dx F F F x dx t F x t T )
x
dx t x t
t
ψ
µαα
∂=+= + − = +−
∂
Suy ra:
22
00
22
y
FTT
tx x x
ψ
αψ
µ
∂
∂∂
== =
∂∂ ∂ ∂
∂
(3)
(L−u ý :
x
ψ
α
∂
=∂).
3) Ph−¬ng tr×nh truyÒn sãng:
Tõ ph−¬ng tr×nh (3), suy ®−îc ph−¬ng tr×nh truyÒn sãng §al¨mbe:
22
222
10
x
ct
ψψ
∂∂
−
∂∂
=
(4) víi: 0
T
c
µ
=
§¹i l−îng 0
T
c
µ
=, cã thø nguyªn cña vËn tèc vµ ®Æc tr−ng cña sù truyÒn sãng trªn d©y.
4) C¸c ph−¬ng tr×nh liªn kÕt:
49
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Ph−¬ng tr×nh truyÒn sãng (4) ®−îc suy tõ hai ph−¬ng tr×nh sau ®©y liªn kÕt Fy(x,t) vµ ψ(x,t):
2
2
00
1y
y
F
tx
FT T
x
ψ
µ
ψ
α
∂
⎧∂=
⎪
⎪∂∂
⎨∂
⎪==
⎪∂
⎩
(5)
Víi (,)
v( , )
x
t
xt t
ψ
∂
=∂ lµ vËn tèc dÞch chuyÓn ngang, ph−¬ng tr×nh (5) trë thµnh :
0
((,)
v(x,t) 1
(- ( , )) v( , )
y
y
)
F
xt
t
Fxt
x
x
t
T
tx
µ
∂−
⎧∂=−
⎪∂∂
⎪
⎨∂∂
⎪=−
⎪∂∂
⎩
(6)
HÖ ph−¬ng tr×nh (6), liªn kÕt biÕn ®æi cña vËn tèc ngang v(x,t) vµ thµnh phÇn ngang (,)
y
F
xt cña
lùc c¨ng d©y , ®−îc gäi lµ c¸c ph−¬ng tr×nh liªn kÕt. (,)Fxt
Nh− vËy, mét biÕn d¹ng cña sîi d©y lµm xuÊt hiÖn mét lùc (,)
y
F
xt , b¶n th©n lùc ®ã cã thÓ kÐo
theo mét vËn tèc dÞch chuyÓn... ChÝnh mèi liªn kÕt nµy lµ c¬ së cña hiÖn t−îng lan truyÒn sãng
trªn sîi d©y.
§2. NghiÖm sãng ph¼ng ch¹y cña ph−¬ng tr×nh §al¨mbe :
• Trªn ®©y, ta ®· biÕt r»ng c¸c sãng () ( )
x
fu ft c
=
− vµ (v) = g( )
x
gt
c
+
lµ c¸c nghiÖm cña
ph−¬ng tr×nh §al¨mbe mét chiÒu
22
222
10
xct
ψψ
∂∂
−
=
∂∂
. Cã thÓ quan s¸t ®−îc sù lan truyÒn cña hai
sãng nµy trªn d©y.
• Ng−êi ta chøng minh r»ng nghiÖm tæng qu¸t cña ph−¬ng tr×nh §al¨mbe ®−îc viÕt d−íi d¹ng
tæng cña hai nghiÖm f(u) vµ g(v):
(,) (,) () (v)
x
tuvfug
ψ
ψ
==+
víi: (,) x
uuxt tc
=
=− vµ vv(,) x
xt t c
=
=+ (7)
NghiÖm ()
x
ft c
− m« t¶ sãng ph¼ng ch¹y lan truyÒn víi vËn tèc c theo ph−¬ng Ox theo chiÒu x
t¨ng. NghiÖm ()
x
gt c
+ m« t¶ sãng ph¼ng ch¹y lan truyÒn víi vËn tèc c theo ph−¬ng Ox theo chiÒu
x gi¶m.
§3. NghiÖm sãng ph¼ng ch¹y ®¬n s¾c cña ph−¬ng tr×nh §al¨mbe:
1) NghiÖm h×nh sin cña ph−¬ng tr×nh §al¨mbe:
Cã thÓ t×m nghiÖm cña ph−¬ng tr×nh Dalembert phô thuéc vµo thêi gian theo d¹ng h×nh sin.
Sö dông ký hiÖu phøc, nghiÖm h×nh sin cã d¹ng: (,) ()it
x
txe
ω
ψϕ
= (2)
TÝnh
2
2
x
ψ
∂
∂;
2
2
t
ψ
∂
∂(3) vµ thay vµo ph−¬ng tr×nh truyÒn sãng, suy sa:
22
22
() () 0
xx
xc
ϕωϕ
∂+=
∂
(2 ) NghiÖm sãng ph¼ng ch¹y h×nh sin cã d¹ng : + D¹ng thùc : 0
(,) cos( )xt t kx
ψ
ψω ϕ
=
−+
+ D¹ng phøc : ()
0
(,)xt itkx
e
ω
ψ
ψ
=− víi 00
i
e
ϕ
ψ
ψ
=, trong ®ã k cã thÓ d−¬ng hay ©m. Do ®ã, cã thÓ viÕt :
0
(,) ikx i t
x
tee
ω
ψ
ψ
−
= hay (,) ()it
x
txe
ω
ψ
ϕ
= víi 0
() ikx
x
e
ϕψ
−
=)
50