1
Px!phangiakhue
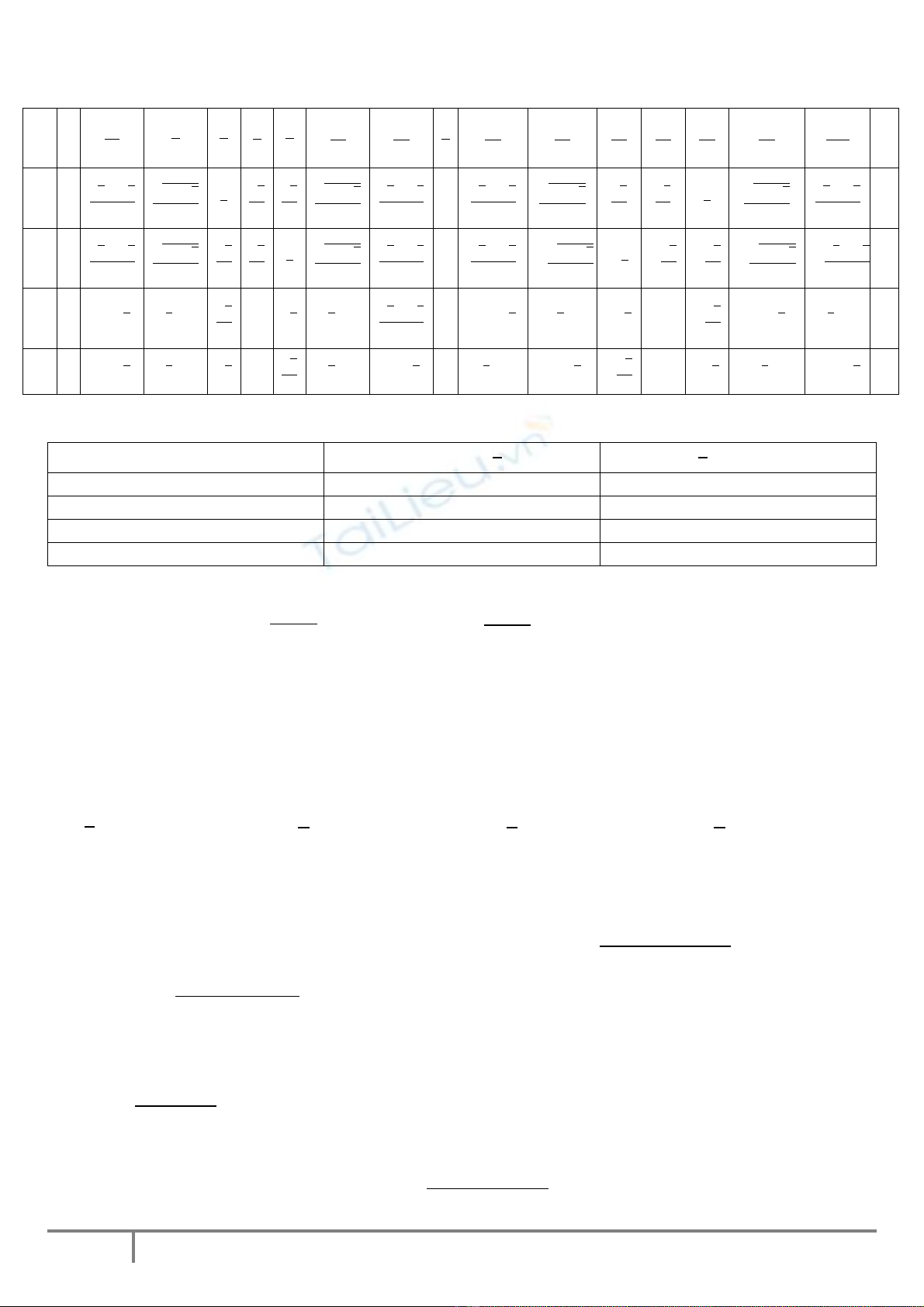
GÓC VÀ CUNG LƯỢNG GIÁC
0













sin
0
√
6
−
√
2
4
2
−
√
2
2
1
2
√
2
2
√
3
2
2
+
√
2
2
√
6
+
√
2
4
1
√
6
+
√
2
4
2
+
√
2
2
√
3
2
√
2
2
1
2
2
−
√
2
2
√
6
−
√
2
4
0
cos
1
√
6
+
√
2
4
2
+
√
2
2
√
3
2
√
2
2
1
2
2
−
√
2
2
√
6
−
√
2
4
0
√
2
−
√
6
4
−
2
−
√
2
2
−
1
2
−
√
2
2
−
√
3
2
−
2
+
√
2
2
−
√
6
+
√
2
4
-1
tan
0
2
−
√
3
√
2
−
1
√
3
3
1
√
3
√
2
+
1
√
6
−
√
2
4
|
−
2
−
√
3
−
√
2
−
1
−
√
3
-1
−
√
3
3
1
−
√
2
√
3
−
2
0
cot
|
2
+
√
3
√
2
+
1
√
3
1
√
3
3
√
2
−
1
2
−
√
3
0
√
3
−
2
1
−
√
2
−
√
3
3
-1
−
√
3
−
√
2
−
1
−
2
−
√
3
|
Dấu của các giá trị lượng giác:
0 < α <
< α < π
c
osα
+
-
s
inα
+
+
tanα
+
-
cotα
+
-
Các đẳng thức lượng giác cơ bản:
sin
2
+ cos
2
= 1
tan.cot = 1 1
cos
2
=1+
tan
2
1
sin
=1+cot
Hàm số lượng giác của cung đối nhau
:
sin −!= −sin cos −!= cos tan −!= −tan cot −!= −cot
Hàm số lượng giác của các cung bù nhau:
sin "−!
= sin
cos "−!
=
−cos
tan "−!
=
−tan
cot "−!
=
−cot
Hàm số lượng giác của cung phụ nhau:
sin "
2−!= cos
cos "
2−!
=
sin
tan "
2−!
=
cot
cot "
2−!
=
tan
CÔNG THỨC LƯỢNG GIÁC
Công thức cộng:
sin ± $!
=
sincos$± cossin$
cos ± $!
=
coscos$∓ sinsin$
tan ± $!= tan ± tan$
1∓tan.tan$
cot ±$!=±cotcot$−1
cot±cot$
Công thức nhân đôi:
sin2 =2sin.cos
tan2 = 2tan
1−tan
cos2 = cos
−sin
=2cos
−1=1−2sin
Công thức nhân ba:
cos3 =4cos
&
−3cos tan3 = 3tan−tan
&
1−3tan
sin3= 3sin−4sin
&
2
Px!phangiakhue
Công thức biến đổi tích thành tổng:
cos.cos$=1
2'cos +$!+cos −$!(
sin.sin$=1
2'cos −$!−cos +$!(
sin.cos$=1
2'sin +$!+sin −$!(
cos.sin$=1
2'sin +$!−sin −$!(
Công thức biến đổi tổng thành tích:
cos+cos$=2cos+$
2cos−$
2
cos−cos$=−2sin+$
2sin−$
2
sin+sin$=2sin+$
2cos−$
2
sin−sin$=2cos+$
2sin−$
2
tan+tan$=sin +$!
cos.cos$
cot+cot$=sin +$!
sin.sin$
tan−tan$=sin −$!
cos.cos$
cot−cot$=sin $−!
sin.sin$
Công thức hạ bậc:
sin
=1−cos2
2
cos
=1+cos2
2
sin
&
=3sin−sin3
4
cos
&
=3cos+cos3
4
Công thức rút gọn:
asin)+*cos)=√+
+*
sin )+! ,ớ- cot=
.
/
= √+
+*
cos )−! ,ớ- tan=
/
.
asin)−*cos)=+
+*
sin )−! ,ớ- cot=*
+
=√+
+*
cos )+! ,ớ- tan=
/
.
Hệ quả:
sin+cos=√2sin0+"
41=√2cos0−"
41
sin−cos=√2sin0−"
41=−√2cos0+"
41
tan+cot= 2
sin2
tan−cot=−2cot2
Công thức tính sinα, cosα, tanα theo
2=234
5
sin= 26
1+6
cos=1−6
1+6
tan= 26
1−6
HỆ THỨC LƯỢNG TRONG TAM GIÁC
Định lý hàm số cosin:
+
=*
+7
−2*7cos8
*
=+
+7
−2+7cos9 7
=+
+*
−2+*cos:
3
Px!phangiakhue
Định lý hàm số sin:
+
sin8=*
sin9=7
sin:=2;
Định lý đường trung tuyến
:
*
+7
=2<
/
++
2
+
+7
=2<
.
+*
2
+
+*
=2<
=
+7
2
Định lý đường phân giác:
Phân giác trong
>
?
=2*7cos8
2
*+7 = 2*7@ @−+!
*+7
>
A
=2+7cos9
2
++7 = 2+7@ @−*!
++7
>
B
=2+*cos:
2
++* = 2+*@ @−7!
++*
Phân giác ngoài
>′
?
=2*7cos8
2
|*−7|
>′
A
=2+7cos9
2
|+−7|
>′
B
=2+*cos:
2
|+−*|
Định lý hình chiếu:
a = b.
cos
C + c.
cos
B
b = c.
cos
A + a.
cos
C
c = a.
cos
B + b.
cos
A
Công thức về diện tích:
E=
F
*7sin8=
F
+7sin9=
F
+*sin:
E= +*7
4;
E=@G=@ @−+!tan8
2=@ @−*!tan9
2=@ @−7!tan:
2
E=@ @−+! @−*! @−7!
E=1
2+ℎ
/
=1
2*ℎ
.
=1
27ℎ
=
E=2;
sin8sin9sin:
E=+
sin9sin:
2sin8 =*
sin8sin:
2sin9 =7
sin8sin9
2sin:
E=G
/
@−+!=G
.
@−*!=G
=
@−7!
E=3
4@
I
@
I
−<
/
! @
I
−<
.
! @
I
−<
=
! Jớ- @
I
=1
2 <
/
+<
.
+<
=
!
E=ℎ
/
ℎ
.
4.1
K@
I
@
I
−ℎ
/
! @
I
−ℎ
.
! @
I
−ℎ
/
ℎ
.
ℎ
=
! Jớ- @
I
=1
2Lℎ
/
+ℎ
.
+ℎ
/
ℎ
.
ℎ
=
M
Cho A’, B’, C’ là chân các đường phân giác:
E
?IAIBI
=E 2+*7
++*! *+7! 7++!
Cho H
A
, H
B
, H
C
là chân các đường cao:
E
N
O
N
P
N
Q
=Ecos8cos9cos:
4
Px!phangiakhue
Công thức liên quan đường tròn nội tiếp:
G=E
@=4;sin8
2sin9
2sin:
2= @−+!tan8
2= @−*!tan9
2= @−7!tan:
2
G
/
=@tan8
2 G
.
=@tan9
2 G
=
=@tan:
2
1
G=1
ℎ
/
+1
ℎ
.
+1
ℎ
=
Công thức về góc:
sin8
2=R @−*! @−7!
*7 sin9
2=R @−+! @−7!
+7 sin:
2=R @−+! @−*!
+*
cos8
2=R@ @−+!
*7
cos9
2=R@ @−*!
+7
cos:
2=R@ @−7!
+*
tan8
2=R @−*! @−7!
@ @−+!
tan9
2=R @−+! @−7!
@ @−*!
tan:
2=R @−+! @−*!
@ @−7!
Một số công thức trong tam giác vuông:
+
=*
+7
1
ℎ
=1
*
+1
7
*
=*′+
7
=7′+
ℎ
=*′7′
+ℎ=*7
Một số công thức trong tam giác thường:
AI và AJ là phân giác của
98:
S
thì:
T9
T:=U9
U:=89
8:
H
A
là chân đường cao từ A, O
A
là trung điểm BC:
89
−8:
=29:
V
V
V
V
.W
?
X
?
V
V
V
V
V
V
V
H’ là trực tâm tam giác, H
A
là chân đường cao từ A:
X
?
X.X
?
8=X
?
9.X
?
:
Đẳng thức trong tam giác:
sin8+sin9+sin:=4cos8
2.cos9
2.cos:
2
cos8+cos9+cos:=4sin8
2.sin9
2.sin:
2+1
tan8+tan9+tan:=tan8.tan9.tan:
cot8.cot9+cot9.cot:+cot8.cot:=1
tan8
2.tan9
2+tan9
2.tan:
2+tan8
2.tan:
2=1
cot8
2+cot9
2+cot:
2=cot8
2.cot9
2.cot:
2
Bất đẳng thức trong tam giác:
sin8+sin9+sin:≤3√3
2
1<cos8+cos9+cos:≤3
2
1<sin8
2+sin9
2+sin:
2≤3
2
2<cos8
2+cos9
2+cos:
2≤3√3
2
sin8.sin9.sin:≤3√3
8
sin8
2.sin9
2.sin:
2≤1
8
cos8.cos9.cos:≤1
8
cos8
2.cos9
2.cos:
2≤3√3
8
5
Px!phangiakhue
sin
8+sin
9+sin
:≤9
2
tan++tan9+tan:≥3√3
tan8
2+tan9
2+tan:
2≥√3
tan8
2.tan9
2.tan:
2≤1
3√3
cot8+cot9+cot:≥√3
cot8
2+cot9
2+cot:
2≥3√3
HỆ THỨC TRONG TỨ GIÁC
E=R @−+! @−*! @−7! @−^!−+*7^cos
9+_
2 Jớ- @=++*+7+^
2
E=8:.9_.sin
2 Jớ-  >à aó7 a-ữ+ ℎ+- đườda 7ℎéf
Nếu tứ giác nội tiếp thì:
Tích hai đường chéo bằng tổng tích hai cạnh đối.
E= @−+! @−*! @−7! @−^!
---------®---------
VI PHÂN
Hàm lũy thừa:
^ )
g
!=)
ghF
^)
^ +)+*!=+ ^)
^L1
)M=−^)
)
^L1
)
i
M=−d)
ihF
)
i
^)
^j√)k= ^)
2√)
^j√)
l
k= ^)
d√)
ihF
l
Hàm lượng giác:
^ sin)!=cos) ^)
^ cos)!=−sin) ^)
^ tan)!=^)
cos
)= 1+tan
)! ^)
^ cot)!=− ^)
sin
)
Hàm lượng giác ngược:
^ sin
hF
)!=^)
√1−)
^ cos
hF
)!=− ^)
√1−)
^ tan
hF
)!=^)
1+)
^ cot
hF
)!=− ^)
1+)
Hàm mũ và logarithme:
^ ln)!=^)
)
^ log
/
)!=^)
)ln+
^ o
p
!=o
p
^)
^ +
p
!=+
p
ln+ ^)