- 1 - Tóm tắt công thức
- 1 - XSTK
Tóm tắt công thức Xác Suất - Thống Kê
I. Phần Xác Suất
1. Xác suất cổ điển
Công thức cộng xác suất: P(A+B)=P(A)+P(B)-P(AB).
A1, A2,…, An xung khắc từng đôi
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
Ta có
o A, B xung khắc
P(A+B)=P(A)+P(B).
o A, B, C xung khắc từng đôi
P(A+B+C)=P(A)+P(B)+P(C).
o
( ) 1 ( )
P A P A
.
Công thức xác suất có điều kiện:
( )
( / )
( )
P AB
P A B
P B
,
( )
( / )
( )
P AB
P B A
P A
.
Công thức nhân xác suất: P(AB)=P(A).P(B/A)=P(B).P(A/B).
A1, A2,…, An độc lập với nhau
P(A1.A2.….An)=P(A1).P(A2).….P( An).
Ta có
o A, B độc lập
P(AB)=P(A).P(B).
o A, B, C độc lập với nhau
P(A.B.C)=P(A).P(B).P(C).
Công thức Bernoulli: ( ; ; )
k k n k
n
, với p=P(A): xác suất để biến cố A
xảy ra ở mỗi phép thử và q=1-p.
Công thức xác suất đầy đủ - Công thức Bayes
o Hệ biến cố gồm n phần tử A1, A2,…, An được gọi là một phép phân
hoạch của
1 2
. ; , 1,
...
i j
n
A A i j i j n
A A A

o Công thức xác suất đầy đủ:
1 1 2 2
1
( ) ( ). ( / ) ( ). ( / ) ( ). ( / ) ... ( ). ( / )
n
i i n n
i
P B P A P B A P A P B A P A P B A P A P B A
o Công thức Bayes:
( ). ( / )
( / ) ( )
i i
i
P A P B A
P A B P B
với 1 1 2 2
( ) ( ). ( / ) ( ). ( / ) ... ( ). ( / )
n n
P B P A P B A P A P B A P A P B A
2. Biến ngẫu nhiên
a. Biến ngẫu nhiên rời rạc
Luật phân phối xác suất
với
( ), 1, .
i i
p P X x i n
Ta có:
1
1
n
i
ip
và f(
{a f(X) b}=
i
i
a x b
P p

X x1 x2 … xn
P p1 p2 … pn
- 2 - Tóm tắt công thức
- 2 - XSTK
Hàm phân phối xác suất
( ) ( )
i
X i
x x
F x P X x p
Mode
0 0
ModX max{ : 1, }
i
x p p i n
Median
0,5
( ) 0,5
MedX ( ) 0,5
0,5
i e
i e
i
x x
e
eei
x x
p
P X x
xP X x p
Kỳ vọng
1 1 2 2
1
( . ) . . ... .
n
i i n n
i
EX x p x p x p x p
1 1 2 2
1
( ( )) ( ( ). ) ( ). ( ). ... ( ).
n
i i n n
i
E X x p x p x p x p
Phương sai
2 2
( ) ( )
VarX E X EX
với 2 2 2 2 2
1 1 2 2
1
( ) ( . ) . . ... .
n
i i n n
i
E X x p x p x p x p
b. Biến ngẫu nhiên liên tục.
f(x) là hàm mật độ xác suất của X
( ) 1


f x dx
,
{a X b} ( ).
b
a
P f x dx
Hàm phân phối xác suất
( ) ( ) ( )
x
X
F x P X x f t dt

Mode
0
ModX x
Hàm mật độ xác suất f(x) của X đạt cực đại tại x0.
Median
1 1
( ) ( )
2 2
e
x
e X e
MedX x F x f x dx

.
Kỳ vọng
EX . ( )
x f x dx


.
( ( )) ( ). ( )
E X x f x dx


- 3 - Tóm tắt công thức
- 3 - XSTK
Phương sai
2 2
( ) ( )
VarX E X EX
với 2 2
EX . ( )
x f x dx


.
c. Tính chất
-
( ) , ( ) 0
E C C Var C
, C là một hằng số.
-2
( ) , ( )
E kX kEX Var kX k VarX
-( )
E aX bY aEX bEY
- Nếu X, Y độc lập thì 2 2
( ) . , ( )
E XY EX EY Var aX bY a VarX b VarY
-( )
X VarX
: Độ lệch chuẩn của X, có cùng thứ nguyên với X và EX.
3. Luật phân phối xác suất
a. Phân phối Chuẩn
2
( ~ ( ; ))
X N
( )X
, EX=ModX=MedX=
,
2
VarX
Hàm mđxs
2
2
( )
2
1
( , , ) 2
x
f x e

Với
0, 1:
2
2
1
( ) 2
x
f x e
(Hàm Gauss)
(a X b) ( ) ( )
b a
P
với
2
2
0
1
( ) 2
t
x
x e dt
(Hàm Laplace)
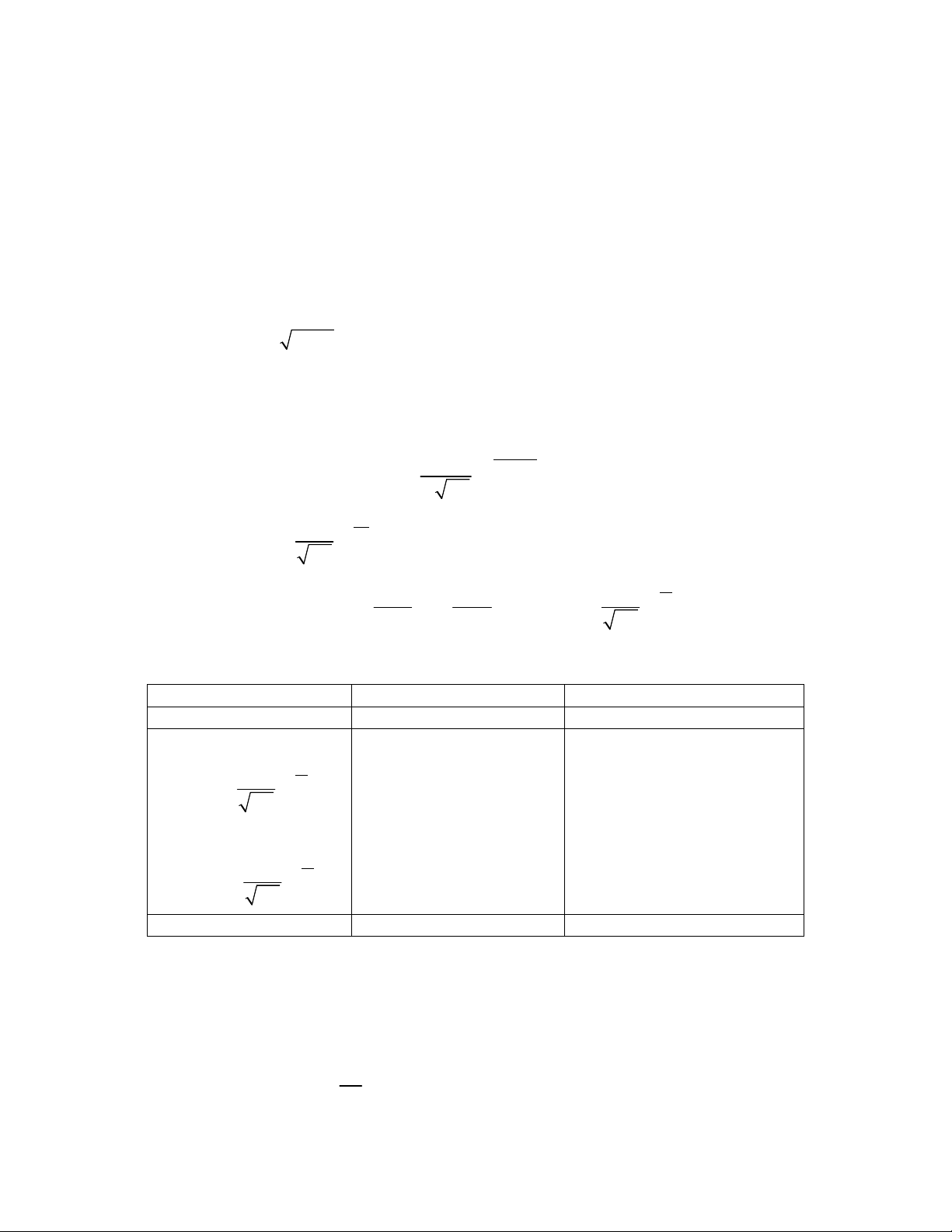
Cách sử dụng máy tính bỏ túi để tính giá trị hàm Laplace, hàm phân phối
xác suất của phân phối chuẩn chuẩn tắc
Tác vụ Máy CASIO 570MS Máy CASIO 570ES
Khởi động gói Thống kê Mode…(tìm)…SD Mode…(tìm)…STAT 1-Var
Tính 2
2
0
1
( ) 2
t
x
x e dt
2
2
1
( ) 2

t
x
F x e dt
Shift 3 2 x ) =
Shift 3 1 x ) =
Shift 1 7 2 x ) =
Shift 1 7 1 x ) =
Thoát khỏi gói Thống kê Mode 1 Mode 1
Lưu ý:
( ) 0,5 ( )
F x x
b. Phân phối Poisson
( ~ ( ))
X P
( )X
, EX . odX=k -1 kVarX M

(X=k)=e ,
!
k
P k
k

- 4 - Tóm tắt công thức
- 4 - XSTK
c. Phân phối Nhị thức
( ~ ( ; ))
X B n p
( ) {0..n}
X
, EX=np, VarX=npq, ModX=k
( 1) 1 ( 1)
n p k n p
(X=k)=C . . ,q p 0 ,
k k n k
n
P p q k n k
Nếu
( 30;0,1 0,9; 5, 5)
n p np nq thì
2
~ ( ; ) ( ; )
X B n p N với
. ,
n p npq
1
(X=k) ( ), 0 ,
k
P f k n k
 
(a X<b) ( ) ( )
b a
P
Nếu
( 30, 5)

n p np thì
~ ( ; ) ( )
X B n p P với
np
(X=k) e ,
!
k
P k
k

Nếu
( 30, 0,9, 5)
n p nq
(X=k) e ,
( )!
n k
P k
n k
với
nq
d. Phân phối Siêu bội
( ~ ( ; ; ))
A
X H N N n
( ) {max{0; ( )}..min{n;N }}
A A
X n N N
EX=np, VarX=npq
1
N n
N
với
A
N
p
N
, q=1-p.
( 1)( 1) 2 ( 1)( 1) 2
1
2 2
A A
N n N n
ModX k k
N N
.
(X=k)= , ( )
A A
k n k
N N N
n
N
C C
P k X
C

Nếu
20
N
n
thì
~ ( ; ; ) ( ; )
A
X H N N n B n p
với
A
N
p
N
.
(X=k) C . . , ( ), 1
k k n k
n
P p q k X q p

.
- 5 - Tóm tắt công thức
- 5 - XSTK
X
Y
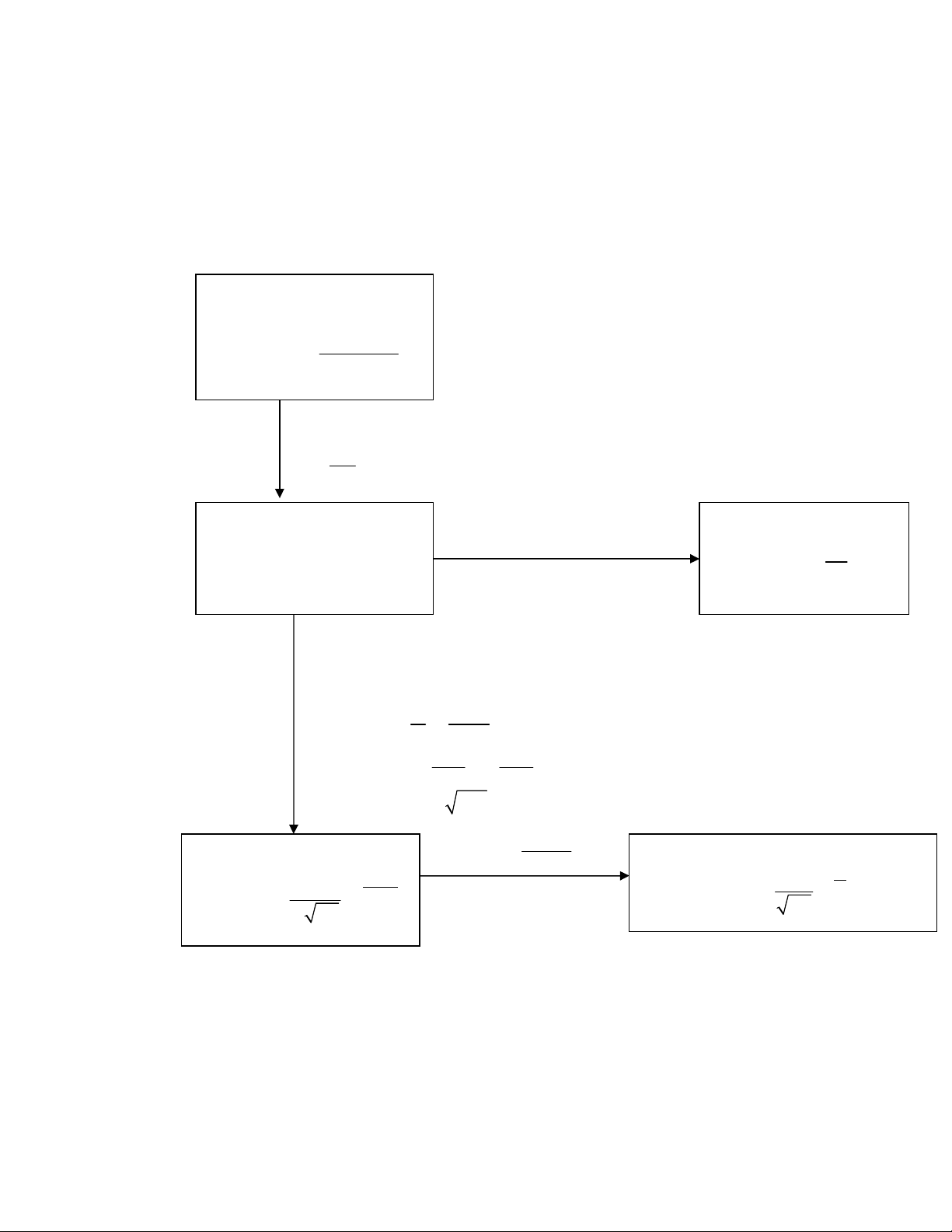
Sơ đồ tóm tắt các dạng phân phối xác suất thông
dụng:
n
30, np<5
p
0,1
=np
N>20n
p=
A
N
N
, q=1-p
n
30, np
5
, nq
5
0,1<p<0,9
1
( ) ( )
k
P X k f
( ) ( ) ( )
b a
P a X b
với ,
np npq

Siêu bội: X~H(N;NA;n)
.
( )
A A
k n k
N N N
n
N
C C
P X k C
Poisson: X~
( )
P
( )
!
k
P X k e
k
Nhị thức: X~B(n;p)
( ) . .
k k n k
n
P X k C p q
Chuẩn: X~
2
( ; )
N
2
2
( )
2
1
( ; ; ) .
2
x
f x e

Chuẩn chuẩn tắc: Y~ N(0;1)
2
2
1
( ) .
2
y
f y e