HCMUT-CNCP LỚP XÁC SUẤT THÔNG KÊ HK242 (nội bộ)
PHẦN 1: XÁC SUẤT
Định lý bernoully
Thực hiện n phép thử độc lập với nhau, xác suất thành công của một phép
thử không đổi là p. Xác suất có đúng k phép thử thành công trong n lần thử
là Cn
kpk.(1−p)n−k
Công thức xác suất đầy đủ
Cho {A1, A2, A3} là hệ biến cố đầy đủ khi đó
P(A1)+P(A2)+P(A3) = 1
P(F)=P(A1).P(F
A1)+P(A2).P(F
A2)
+P(A3).P(F
A3)
Công thức Bayes
P(Ai
F)=P(Ai).P(F
Ai)
P(F) Với i=1,2,3..
Hàm mật độ xác suất
➢ ∫f(x)dx=1
+∞
−∞
➢ f(x)≥0
➢ P(X=xi)≈0 (gần bằng 0)
➢ P(a≤X≤b)=∫f(x)
b
adx
Một số trường hợp hay dùng
➢ P(X=a)=f(a)
➢ P(X≤a)=∫f(x)dx
a
−∞ =
1−∫f(x)dx
+∞
a
➢ P(X≥a)=∫f(x)dx
+∞
a=
1−∫f(x)dx
a
−∞
➢ P(a≤X≤b)=∫f(x)dx
b
a
Tính chất hay thi:
Tính chất của E(X)
• E(aX+b)=aE(X)+b
• E(X+Y)=E(X)+E(Y)
• E(X.Y)=E(X).E(Y) nếu
X, Y là 2 biến cố độc lập
Tính chất phương sai D(X)
• D(aX+b)=a2D(X)
• D(X+Y)=D(X)+
D(Y) nếu X và Y độc lập
• D(X−Y)=D(X+Y)
Phân phối mũ
Biến ngẫu nhiên X có phân phối mũ khi có hàm mật độ có dạng
f(x)={λe−λx,x≥0
0, x<0
Trong đó: λ= 1
E(X); Ký hiệu: X~E(λ)
Lưu ý cần nhớ
• D(X)= 1
λ2
• Med(X)=ln (2)
λ
Đặc biệt: Y = min{𝑋1,𝑋2,𝑋3,…𝑋𝑛}=> λ=λ1+⋯+λn
Phân phối Poisson
Biến ngẫu nhiên rời rạc X có phân phối Poisson
P(X=k)=e−λ.λk
k! , kí hiệu: X~P(λ). Trong đó E(X)=D(X)=λ
Đặc biệt:𝑌 = 𝑋1+𝑋2+𝑋3+⋯=> λ=λ1+λ2+⋯+λn
Phân phối chuẩn f(x)=1
σ√2πe−(x−a)2
2σ2
Trong đó: a=E(X), σ2=D(X), Kí hiệu: X~N(a,σ2)
Hàm phân phối xác suất của biến cố ngẫu nhiên có phân phối chuẩn chỉnh
tắc F(x)=Φ(x)=∫ 1
√2πe−t2
2dt
x
−∞
P(m≤X≤n)=∫ 1
σ√2πe−(x−a)2
2σ2dx
n
m
=∫ 1
√2πe−x2
2dx=Φ(n−a
σ)−Φ(m−a
σ)
n−a
σ
m−a
σ
Cách bấm máy tính tìm 𝚽(𝐚)
Casio 570, Vinacal
Casio 580
Step1: Bật tính năng thống
kê
Mode →3→ 1→ AC
Step2: Tìm 𝛷(𝑎)
Nhấn Shift →1→5→1
(P)
Nhập P(a)
Step 1: Bật tính năng thống kê
Menu → 6→ AC
Step2: Tìm 𝛷(𝑎)
Option → 𝛻 → 4
Nhập P(a)
Đặc biệt: 𝑌 = 𝑋1+𝑋2+𝑋3+⋯ đều là PP chuẩn thì 𝑌~𝑁 (𝑎1+𝑎2+
𝑎3+..,𝜎12+𝜎22+𝜎32+..)
Phân phối nhị thức
Đại lượng ngẫu nhiên X có phân phối nhị thức thì
𝑃(𝑋=𝑘)=𝐶𝑛
𝑘𝑝𝑘.(1−𝑝)𝑛−𝑘
Kí hiệu: : 𝑋~𝐵(𝑛,𝑝)
Một số tính chất
𝐸(𝑋)=𝑛𝑝,𝐷(𝑋)=𝑛𝑝(1−𝑝)
Lưu ý:
• Nếu n rất lớn (n>30) và p ≤ 5% ta xấp sỉ phân phối nhị
thức về phân phối Poisson. Với 𝜆=𝐸(𝑋)=𝑛𝑝
• Nếu n rất lớn (n>30) và p > 5% ta xấp sỉ phân phối nhị
thức về phân phối chuẩn. Với 𝑎=𝐸(𝑋)=𝑛𝑝 ,𝜎2=
𝐷(𝑋)=𝑛𝑝(1−𝑝), nhưng khác là phải tính theo công
thức PP chuẩn hiệu chỉnh sau 𝑃(𝑚≤𝑋≤𝑛)=
Φ(n+0,5−a
σ)−Φ(m−0,5−a
σ)
Đặc biệt: 𝑥1~𝐵(𝑛1;𝑝),𝑋2~𝐵(𝑛2;𝑝), 𝑋3~𝐵(𝑛3;𝑝),….. 𝑋𝑛~𝐵(𝑛𝑛;𝑝)
thì 𝑌=𝑋1+𝑋2+𝑋2+⋯𝑋𝑛 thì 𝑋𝑛~𝐵(𝑛1+𝑛2+⋯+𝑛𝑛;𝑝)
Phân phối đều
Đại lượng ngẫu nhiên X gọi là có phân phối đều trên đoạn [a, b] nếu
hàm mật độ của X là 𝑓(𝑥)={ 1
𝑏−𝑎, 𝑥∈[𝑎,𝑏]
0, 𝑥≠[𝑎,𝑏]
Kí hiệu: 𝑋~𝑈(𝑎,𝑏) và 𝐸(𝑋)=𝑎+𝑏
2,𝐷(𝑋)=(𝑏−𝑎)2
12
Phân phối siêu bội
Cho đại lượng ngẫu nhiên X gọi là phân phối siêu bội nếu tồn tại các
số tự nhiên M, N sao cho 𝑛≤𝑀≤𝑁 thỏa
𝑃(𝑋=𝑘)=𝐶𝑀
𝑘𝐶𝑁−𝑀
𝑛−𝑘
𝐶𝑁
𝑛
Kí hiệu: 𝑋~𝐻(𝑁,𝑀,𝑛), 𝐸(𝑋)~𝑛𝑝, 𝐷(𝑋)=𝑛𝑝𝑞𝑁−𝑛
𝑁−1
Với: 𝑝=𝑀
𝑁,𝑞=1−𝑝
Định lý giá trị trung bình
Cho các biến ngẫu nhiên 𝑥1+x2+𝑥3+⋯x𝑛 có cùng quy luật phân
phối bất kì và có cùng kì vọng a=E(X) và phương sai 𝜎2.
• Với BNN Y = 𝑥1+x2+𝑥3+⋯x𝑛 thì BNN Y sẽ có quy
luật phân phối chuẩn 𝑌~𝑁(𝑛.𝑎;n.𝜎2).
• Với BNN Y=𝑌=𝑥1+x2+𝑥3+⋯x𝑛
𝑛 thì BNN Y sẽ có quy luật
phân phối chuẩn là 𝑌~𝑁(𝑎;𝜎2/𝑛)
PHẦN 2: THỐNG KÊ: Nhắc cách tra bảng:
Tính 𝑧𝛼 dùng bảng phân phối chuẩn tra
ngược giá trị, sao cho
Φ(𝑧𝛼)=1−𝛼=𝛽
Tính 𝑡𝛼
2;𝑛−1 dùng bảng Student tra giá trị tại hàng n-
1 và cột 𝛼
2
Tính 𝑓𝛼𝑘−1;𝑁−𝑘 bằng các tra bảng
fisher với mức ý nghĩa 𝛼, cột 𝑘−1 và hàng
𝑁−𝑘
Khoảng tin cậy, ước lượng
Bài toán ngược tìm n
Dạng
Điều kiện
Loại
Khoảng tin cậy (khoảng ước lượng)
Tỷ lệ
Đối
xứng
𝑝∈( 𝑓− 𝜀;𝑓+𝜀 ) với 𝜀=𝑧𝛼/2.√𝑓(1−𝑓)
√𝑛
Trung
bình
Biết 𝜎2, phân
phối chuẩn
𝜇∈(𝑥− 𝜀;𝑥+𝜀 ) với 𝜀=𝑧𝛼/2.𝜎
√𝑛
Chưa biết 𝜎2,
tìm được s và
n < 30, phân
phối chuẩn
𝜇∈( 𝑥− 𝜀;𝑥+𝜀 ) với 𝜀=𝑡𝛼
2;𝑛−1.𝑠
√𝑛
Chưa biết 𝜎2 ,
tìm được s và
n ≥30
𝜇∈(𝑥− 𝜀;𝑥+𝜀) với 𝜀=𝑧𝛼/2.𝑠
√𝑛
Dạng
Điều kiện
Khoảng tin cậy (khoảng ước lượng)
Bài
toán
trung
bình
Đã cho 𝜎2
𝑛=(𝑧𝛼/2.𝜎
𝜀)2
Chưa cho
𝜎2
𝑛=(𝑧𝛼/2.𝑠
𝜀)2
Tỷ lệ
đã biết 𝑓
𝑛=(𝑧𝛼
2 √𝑓(1−𝑓)
𝜀)2
chưa biết 𝑓
(thường thi
hơn)
𝑛=(𝑧𝛼/2
𝜀)2.0,25
Lưu ý: n làm tròn lên
Kiểm định tỉ lệ một mẫu
Giả thuyết 𝐻𝑜
Giả thuyết đối 𝐻1
Tiêu chuẩn kiểm định
Miền bác bỏ
𝑝=𝑝𝑜
𝑝≠𝑝𝑜
𝑍𝑞𝑠 =𝑓−𝑝𝑜
√𝑝𝑜(1−𝑝𝑜)
𝑛
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝑝=𝑝𝑜 hoặc 𝑝≤𝑝𝑜
𝑝>𝑝𝑜
RR=(𝑧𝛼;+∞)
𝑝=𝑝𝑜 hoặc 𝑝≥𝑃𝑜
𝑝<𝑝𝑜
RR=(−∞;−𝑧𝛼)
Kiểm định trung bình một mẫu
Dạng
Giả thuyết
𝐻𝑜
Giả thuyết đối 𝐻1
Tiêu chuẩn kiểm
định
Miền bác bỏ 𝐻𝑜
Có phân phối chuẩn
và đã biết 𝜎2
𝜇=𝜇𝑜
𝜇≠𝜇𝑜
𝑍𝑞𝑠 =𝑥−𝜇𝑜
𝜎/√𝑛
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝜇>𝜇𝑜
RR=(𝑧𝛼;+∞)
𝜇<𝜇𝑜
RR=(−∞;−𝑧𝛼)
Có phân phối chuẩn
và chưa biết
𝜎2,𝑛<30
𝜇=𝜇𝑜
𝜇≠𝜇𝑜
𝑇𝑞𝑠 =𝑥−𝜇𝑜
𝑠/√𝑛
𝑅𝑅=(−∞;−𝑡𝛼
2;𝑛−1)∪ (𝑡𝛼
2;𝑛−1;+∞)
𝜇>𝜇𝑜
RR=(𝑡𝛼;𝑛−1;+∞)
𝜇<𝜇𝑜
RR=(−∞;−𝑡𝛼;𝑛−1)
Có phân phối tùy ý
chưa biết 𝜎2,𝑛≥
30
𝜇≠𝜇𝑜
𝑍𝑞𝑠 =𝑥−𝜇𝑜
𝑠/√𝑛
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝜇>𝜇𝑜
RR=(𝑧𝛼;+∞)
𝜇<𝜇𝑜
RR=(−∞;−𝑧𝛼)
Kiểm định tỉ lệ 2 mẫu
Giả thuyết
𝐻𝑜
Giả thuyết đối
𝐻1
Tiêu chuẩn kiểm định
Miền bác bỏ
𝑝1=𝑝2
𝑝1≠𝑝2
𝑍𝑞𝑠 =𝑓1−𝑓2
√𝑓(1−𝑓)
𝑛 Với 𝑓=𝑚1+𝑚2
𝑛1+𝑛2; 𝑛= 𝑛1𝑛2
𝑛1+𝑛2
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝑝1=𝑝2
𝑝1>𝑝2
RR=(𝑧𝛼;+∞)
𝑝1=𝑝2
𝑝1<𝑝2
RR=(−∞;−𝑧𝛼)
Kiểm định trung bình 2 mẫu độc lập và phụ thuộc (mẫu phụ thuộc mới xuất hiện trong đề thi HK233)
Dạng
Giả
thuyết
𝐻𝑜
Giả thuyết đối 𝐻1
Tiêu chuẩn kiểm định
Miền bác bỏ 𝐻𝑜
X, Y độc lập Có
phân phối chuẩn và
đã biết 𝜎12, 𝜎22 (z-test)
𝜇1
=𝜇2
𝜇1≠𝜇2
𝑍𝑞𝑠 =𝑥1−𝑥2
√𝜎12
𝑛1+𝜎22
𝑛2
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝜇1>𝜇2
RR=(𝑧𝛼;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑧𝛼)
X,Y độc lập có phân
phối chuẩn và chưa
biết 𝜎12, 𝜎22, và cho
biết rằng 𝜎12= 𝜎22,
𝑛1,𝑛2≤30 (t-test)
𝜇1
=𝜇2
𝜇1≠𝜇2
𝑇𝑞𝑠 =𝑥1−𝑥2
√𝑠𝑝
2
𝑛1+𝑠𝑝
2
𝑛2
với 𝑠𝑝
2=(𝑛1−1)𝑠1
2+ (𝑛2−1)𝑠2
2
𝑛1+𝑛2−2
𝑅𝑅=(−∞;−𝑡𝛼
2;𝑛1+𝑛2−2)∪ (𝑡𝛼
2;𝑛1+𝑛2−2;+∞)
𝜇1>𝜇2
RR=(𝑡𝛼;𝑛1+𝑛2−2;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑡𝛼;𝑛1+𝑛2−2)
X,Y độc lập có phân
phối chuẩn và chưa
biết 𝜎12, 𝜎22, và cho
biết rằng 𝜎12≠ 𝜎22 ,
𝑛1,𝑛2≤30
(t-test)
𝜇1
=𝜇2
𝜇1≠𝜇2
𝑇𝑞𝑠 =𝑥1−𝑥2
√𝑠1
2
𝑛1+𝑠2
2
𝑛2
𝑣= (𝑠1
2
𝑛1+𝑠2
2
𝑛2)2
(𝑠1
2
𝑛1)2
𝑛1−1+(𝑠2
2
𝑛2)2
𝑛2−1
(làm trò chỉ lấ phần nguyên ví dụ 25,6
sẽ thành 25, dùng để tìm RR)
𝑅𝑅=(−∞;−𝑡𝛼
2;𝑣)∪ (𝑡𝛼
2;𝑣;+∞)
𝜇1>𝜇2
RR=(𝑡𝛼;𝑣;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑡𝛼;𝑣)
Lưu ý, để kiểm tra 𝜎12= 𝜎22 hay 𝜎12≠ 𝜎22 khi biết 𝑠1và 𝑠2, ta tính nếu 𝑠1
𝑠2∈[0,5;2] thì 𝜎12= 𝜎22 và ngược lại
X,Y độc lập có phân
phối tùy ý và chưa
biết 𝜎12, 𝜎22 và
𝑛1,𝑛2≥30
(z-test)
𝜇1
=𝜇2
𝜇1≠𝜇2
𝑍𝑞𝑠 =𝑥1−𝑥2
√𝑠12
𝑛1+𝑠2
2
𝑛2
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝜇1>𝜇2
RR=(𝑧𝛼;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑧𝛼)
X,Y phụ thuộc theo
từng cặp X-Y, 2 mẫu
có n mẫu nhỏ 𝑛<30
và đề chưa cho biết
𝜎𝐷
2
(t-test)
𝜇1=
𝜇2
hoặc
𝜇𝐷
=𝜇1
−𝜇2=0
𝜇1𝜇2
Đặ𝑡:𝐷=𝑋1−𝑋2
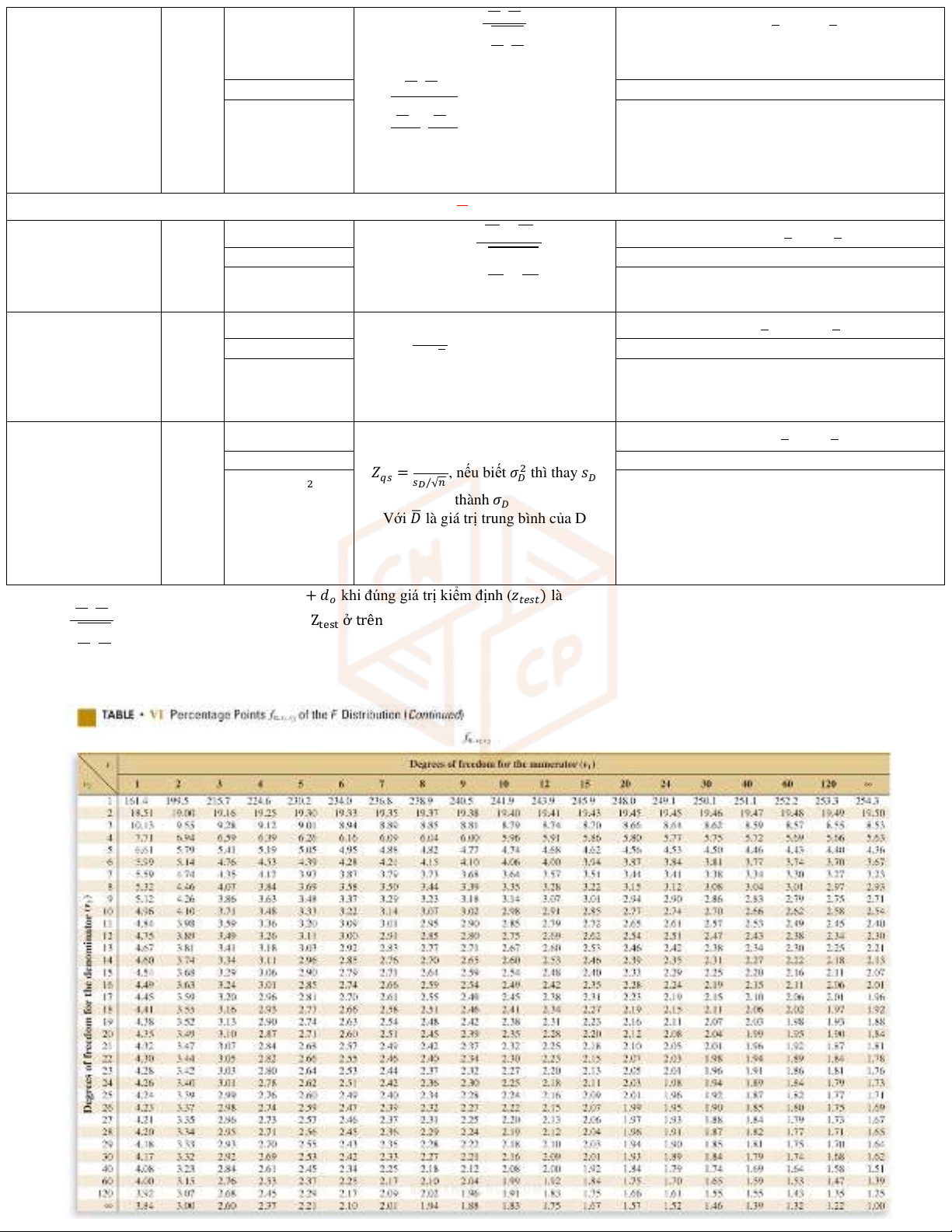
𝑇𝑞𝑠 =𝐷
𝑠𝐷/√𝑛 , nếu biết 𝜎𝐷
2 thì thay 𝑠𝐷
thành 𝜎𝐷
Với 𝐷
là giá trị trung bình của D
𝑅𝑅=(−∞;−𝑡𝛼
2,𝑛−1)∪ (𝑡𝛼
2,𝑛−1;+∞)
𝜇1>𝜇2
RR=(𝑡𝛼,𝑛−1;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑡𝛼,𝑛−1)
X,Y phụ thuộc theo
từng cặp X-Y có
phân phối tùy ý, đã
biết 𝜎𝐷
2 (n<30 hay
𝑛≥30 đều được)
hoặc chưa biết 𝜎𝐷
2
nhưng phải có mẫu
có 𝑛≥30 .
(z-test)
𝜇1=
𝜇2
hoặc
𝜇𝐷
=𝜇1
−𝜇2=0
𝜇1≠𝜇2
Đặ𝑡:𝐷=𝑋1−𝑋2
𝑍𝑞𝑠 =𝐷
𝑠𝐷/√𝑛 , nếu biết 𝜎𝐷
2 thì thay 𝑠𝐷
thành 𝜎𝐷
Với 𝐷
là giá trị trung bình của D
𝑅𝑅=(−∞;−𝑧𝛼
2)∪ (𝑧𝛼
2;+∞)
𝜇1>𝜇2
RR=(𝑧𝛼;+∞)
𝜇1<𝜇2
RR=(−∞;−𝑧𝛼)
Bài toán có thể mở rộng hơn với 𝑯𝟎: 𝜇1=𝜇2+𝑑𝑜 khi đúng giá trị kiểm định (𝑧𝑡𝑒𝑠𝑡) là
𝑍𝑞𝑠 =𝑥1−𝑥2
√𝜎1
2
𝑛1+𝜎2
2
𝑛2 với miền bác bỏ như các b ài Ztest ở trên
Bảng phân phối fisher với alpha=5%
Phân tích phương sai Anova, LSD test và khoảng tin cậy LSD
Phương tích phương sai Anova
Step 1:Giả thuyết kiểm định
•𝐻0:𝜇1=𝜇2=⋯=𝜇𝑘
•𝐻1:∃𝜇𝑖≠𝜇𝑗 (tồn tại ít nhất 1 cặp trung bình tổng thể khác nhau)
Step 2: Miền bác bỏ 𝐻0: 𝑅𝑅=((𝑓𝛼𝑘−1;𝑁−𝑘);+∞)
Xác định 𝑓𝛼𝑘−1;𝑁−𝑘 bằng các tra bảng fisher với mức ý nghĩa 𝛼, cột
𝑘−1 và hàng 𝑁−𝑘 (N là kích thước mẫu gộp)
Step 3: Tính tiêu chuẩn kiểm định 𝐹
Source
of
groups
Tổng bình
phương
chêch lệch
Bậc
tự
do
Phương sai
Tiêu chuẩn
kiểm định 𝐹
Between
groups
SSB (sstr)
k-1
Phương sai giữa các
nhóm: 𝑀𝑆𝐵=𝑆𝑆𝐵
𝑘−1
𝐹=𝑀𝑆𝐵
𝑀𝑆𝑊
Within
groups
SSW (sse)
N-
k
Phương sai trong nội bộ
nhóm: 𝑀𝑆𝑊=𝑆𝑆𝑊
𝑁−𝑘
Total
SST
N-
1
N là kích thước mẫu gộp,
k là số mẫu khảo xác
Trung bình chung của k mẫu :𝑥=∑𝑥𝑖𝑗
𝑖=𝑘,𝑗=𝑛𝑘
𝑖,𝑗=1𝑁
❖ Tính chêch lệch bình phương giữa các nhóm SSB (hay SSG hoặc SSTr)
𝑆𝑆𝐵=∑𝑛𝑖(𝑥𝑖
−𝑥)2
𝑘
𝑖=1 =𝑛1(𝑥1
−𝑥)2+𝑛2(𝑥2
−𝑥)2+⋯+𝑛𝑘(𝑥𝑘
−𝑥)2
❖ Tính tổng chêch lệch bình phương trong nội bộ mẫu SSW (hay SSE)
Mẫu 1
…
Mẫu k
𝑆𝑆1=∑(𝑥1𝑗−𝑥1
)2
𝑘
𝑖=1
Bấm máy: 𝑆𝑆1=𝑠12.(𝑛1−
1)
…
𝑆𝑆𝑘=∑(𝑥𝑘𝑗−𝑥𝑘
)2
𝑘
𝑖=1
Bấm máy: 𝑆𝑆𝑘=𝑠𝑘
2.(𝑛𝑘−1)
❖ Tính tổng chêch lệch bình phương toàn bộ SST (biến thiên toàn phần)
𝑆𝑆𝑇= ∑ (𝑥𝑖𝑗−𝑥)2
𝑖=𝑘,𝑗=𝑛𝑘
𝑖,𝑗=1
Lưu ý, tổng biến thiên do các thành phần sai số ngẫu nhiên gây ra (tổng
bình phương) trong dữ liệu là SSW
Còn tiếp xem ở bên tay phải nhen
Mối quan hệ giữa SSB, SSW, SST: 𝑆𝑆𝑇=𝑆𝑆𝑊+𝑆𝑆𝐺
❖ Tính phương sai toàn bộ:𝑀𝑆𝑇=𝑆𝑆𝑇
𝑁−1
❖ Tính tiêu chuẩn kiểm định F là ∶ 𝐹=𝑀𝑆𝐵
𝑀𝑆𝑊
❖ Hệ số xác định: 𝑅2=𝑆𝑆𝐵
𝑆𝑆𝑇𝑥100%
LSD test
Ta phải kiểm tra từng cặp mẫu theo quy trình sau (𝐶𝑘2 𝑡𝑟ườ𝑛𝑔 ℎợ𝑝)
Giả thuyết
• 𝐻0: 𝜇𝑖=𝜇𝑗
• 𝐻1: 𝜇𝑖≠𝜇𝑗
Giả thuyế 𝐻0 được bác bỏ nếu |𝑥𝑖
−𝑥𝑗
|>𝐿𝑆𝐷𝑖;𝑗 với
𝐿𝑆𝐷𝑖;𝑗 =𝑡𝛼
2;(𝑁−𝑘)∗√𝑀𝑆𝑊(1
𝑛𝑖+1
𝑛𝑗) (gọi là giá trị thống kê kiểm định)
Cách tính: 𝑡𝛼
2;(𝑁−𝑘): Tra bảng student tại cột 𝛼
2 và hàng N-k
Thường bài toán sẽ cho 𝑛𝑖=𝑛𝑗=𝑛 thì 𝐿𝑆𝐷𝑖;𝑗 =𝑡𝛼
2;(𝑁−𝑘)∗√2𝑀𝑆𝑊
𝑛
Kết luận:
|𝑥𝑖
−𝑥𝑗
|>𝐿𝑆𝐷𝑖;𝑗 thì bác bỏ 𝐻0 có nghĩa là 𝜇𝑖≠𝜇𝑗
o 𝑥𝑖
>𝑥𝑗
kết luận 𝜇𝑖>𝜇𝑗
o 𝑥𝑖
<𝑥𝑗
kết luận 𝜇𝑖<𝜇𝑗
|𝑥𝑖
−𝑥𝑗
|≤ 𝐿𝑆𝐷𝑖;𝑗 thì không kết luận được có sự khác
biệt giữa 𝜇𝑖,𝜇𝑗
Khoảng ước lượng LSD với độ tin cậy 1-𝜶
Ta phải kiểm tra từng cặp mẫu theo quy trình sau (𝐶𝑘2 𝑡𝑟ườ𝑛𝑔 ℎợ𝑝)
Xác định khoảng ước lượng LSD cho độ chênh lệch (𝜇𝑖−𝜇𝑗):
(𝑥𝑖
−𝑥𝑗
)±𝐿𝑆𝐷𝑖;𝑗
Với giá trị thống kê kiểm định 𝐿𝑆𝐷𝑖;𝑗 =𝑡𝛼
2;(𝑁−𝑘)∗√2𝑀𝑆𝑊
𝑛
Kết luận
• Nếu khoảng ước lượng chứa số 0 thì không kết luận được
có sự khác biệt giữa 𝜇𝑖,𝜇𝑗
• Nếu khoảng ước lượng không chứa số 0 thì ta nói có sự
khác biệt giữa hai giá trị trung bình 𝜇𝑖 và 𝜇𝑗
o (𝑥𝑖
−𝑥𝑗
)±𝐿𝑆𝐷𝑖;𝑗 <0: 𝜇𝑖< 𝜇𝑗
o (𝑥𝑖
−𝑥𝑗
)±𝐿𝑆𝐷𝑖;𝑗 >0: 𝜇𝑖> 𝜇𝑗
Hồi quy tính tuyến
1.Đặc trưng của mẫu:
• 𝑥=1
𝑛∑𝑥𝑖
𝑛
𝑖=1 , 𝑠𝑥2=1
𝑛−1∑(𝑥𝑖−
𝑛
𝑖=1
𝑥)2 , 𝑠𝑥2=1
𝑛∑(𝑥𝑖−𝑥)2
𝑛
𝑖=1
• 𝑦=1
𝑛∑𝑦𝑖
𝑛
𝑖=1 và 𝑠𝑦
2=
1
𝑛−1∑(𝑦𝑖−𝑦)2
𝑛
𝑖=1 , 𝑠𝑦
2=
1
𝑛∑(𝑦𝑖−𝑦)2
𝑛
𝑖=1
• 𝑥2
=1
𝑛∑𝑥𝑖2𝑛
𝑖=1
• 𝑥𝑦
=1
𝑛∑𝑥𝑖𝑦𝑖
𝑛
𝑖=1
• 𝑆𝑥𝑥 =∑(𝑥𝑖−𝑥)2=(𝑛−
𝑛
𝑖=1
1)𝑠𝑥2=∑𝑥𝑖2−(∑𝑥𝑖
𝑛
𝑖=1 )2
𝑛
𝑛
𝑖=1
• 𝑆𝑦𝑦 =∑(𝑦𝑖−𝑦)2=(𝑛−
𝑛
𝑖=1
1)𝑠𝑦
2 =∑𝑦𝑖2−(∑𝑦
𝑛
𝑖=1 )2
𝑛
𝑛
𝑖=1
• 𝑆𝑥𝑦 =∑ (𝑥𝑖−𝑥)(𝑦𝑖−𝑦)=
𝑛
𝑖=1
∑𝑥𝑖𝑦𝑖
𝑛
𝑖=1 −1
𝑛∑𝑥𝑖
𝑛
𝑖=1 ∑𝑦𝑖
𝑛
𝑖=1
2.Ước lượng hệ số đường hồi quy
Phương trình hồi quy có dạng
𝑦=𝛽0
+𝛽1
𝑥 hoặc 𝑦=𝑎+𝑏𝑥 (tùy thầy cô kí hiệu khác
nhau)
{
𝛽1
=𝑏=𝑆𝑥𝑦
𝑆𝑥𝑥 =𝑥𝑦
−𝑥.𝑦
𝑛−1
𝑛.𝑠𝑥2=∑𝑥𝑖𝑦𝑖
𝑛
𝑖=1 −1
𝑛∑𝑥𝑖
𝑛
𝑖=1 .∑𝑦𝑖
𝑛
𝑖=1
∑𝑥𝑖2−(∑ 𝑥𝑖
𝑛
𝑖=1 )2
𝑛
𝑛
𝑖=1
𝛽0
=𝑎=𝑦−𝛽1
.𝑥
Kết luận: Ta có phương trình hồi quy có 𝑦=𝛽1
𝑥+𝛽0
hoặc
𝑦=𝑏𝑥+𝑎
Lưu ý: 𝛽0
còn được gói là bình phương bé nhất cho hệ số
chặn của đường thẳng hồi quy (hay hỏi)
3.Tìm covarian, hệ số tương quan mẫu, hệ ố xác đị
𝑹𝟐
và ý nghĩa
a/ Hiệp phương sai covarian
𝐶𝑜𝑣(𝑥,𝑦)=𝑥𝑦
−𝑥.𝑦
b/ Hệ số tương quan mẫu
Cho hai biến X, Y để xác định mối quan hệ
giữa X và Y có tuyến tính hay không ta sẽ
học một đại lượng để đo mức độ phụ thuộc
tuyến tính giữa X và Y là 𝑟𝑥𝑦
𝑟𝑥𝑦 =𝑥𝑦
−𝑥𝑦
𝑠𝑥
𝑠𝑦
=𝑆𝑥𝑦
√𝑆𝑥𝑥.𝑆𝑦𝑦
• 𝑠𝑥
2=1
𝑛∑ (𝑥𝑖−𝑥)2
𝑛
𝑖=1 =𝑥2
−(𝑥)2
• 𝑠𝑥
2=1
𝑛∑ (𝑥𝑖−𝑥)2
𝑛
𝑖=1 =𝑥2
−(𝑥)2
Chú ý: −1≤𝑟𝑥𝑦 ≤1
Kết luận:
|𝑟𝑥𝑦|≤0.3: không có mối quan hệ tuyến tính hoặc mối
quan hệ tuyến tính rất yếu
0.3<|𝑟𝑥𝑦|≤0.5: X, Y có mối quan hệ tuyến tính rất yếu
0.5<|𝑟𝑥𝑦|≤0.8: X, Y có quan hệ tuyến tính trung bình
0.8<|𝑟𝑥𝑦|: X, Y có quan hệ tuyến tính mạnh.
Ngoài ra, nếu |𝑟𝑥𝑦|<0 hàm nghịch biến, |𝑟𝑥𝑦|>0 hàm
đồng biến
4.Ước lượng độ lệch chuẩn 𝝈 ( sai số
chuẩn), phương sai 𝟐 của 𝜷𝟏
❖ 𝑠 (độ lệch chuẩn) có ước lượng là
𝑠=√𝑆𝑆𝐸
(𝑛−2)𝑆𝑥𝑥 (đọc lưu ý bên
dưới)
❖ s2(phương sai) có ước lượng là
𝑠2=𝑆𝑆𝐸
(𝑛−2)𝑆𝑥𝑥 (đọc lưu ý bên dưới)
Thể hiện sự biến thiên của các giá trị
y quan xác được với giá trị y ước
lượng được
5.Ước lượng độ lệch chuẩn 𝝈 của sai
số ngẫu nhiên 𝜺
❖ 𝑠 (độ lệch chuẩn) có ước lượng là
𝑠=√𝑆𝑆𝐸
(𝑛−2)
❖ s2(phương sai) có ước lượng là
𝑠2=𝑆𝑆𝐸
(𝑛−2)
6. Ước lượng độ lệch chuẩn 𝝈 ( sai số
chuẩn), phương sai 𝟐 của 𝜷𝟎
❖ 𝑠 (độ lệch chuẩn) có ước lượng là
𝑠=√𝑥2
.𝑆𝑆𝐸
𝑆𝑥𝑥(𝑛−2)
❖ s2(phương sai) có ước lượng là
𝑠2=𝑥2
.𝑆𝑆𝐸
𝑆𝑥𝑥(𝑛−2)
6.Hệ số xác định 𝑹𝟐
❖ Tổng bình phương toàn phần có ý nghĩa đo mức độ biến
động các giá trị 𝑦𝑖 xung quang giá trị trung bình 𝑦
𝑆𝑆𝑇=𝑆𝑦𝑦 =∑(𝑦𝑖−𝑦)2=(𝑛−1)𝑠𝑦
2
𝑛
𝑖=1=∑𝑦𝑖2−(∑ 𝑦
𝑛
𝑖=1 )2
𝑛
𝑛
𝑖=1
❖ Tổng bình phương sai số do sự khác biệt giữa đường hồi
quy mẫu và trung bình 𝑦
𝑆𝑆𝑅=∑(𝑦𝑖
−𝑦)2=𝛽1
.𝑆𝑥𝑦
𝑛
𝑖=1
❖ Tổng bình phương sai số ước lượng có ý nghĩa đô sự chêch
lệch giữa từng giá trị quan sát với giá trị dự đoán
𝑆𝑆𝐸=∑(𝑦𝑖−𝑦𝑖
)2
𝑛
𝑖=1 (xem live để dễ hiểu)
Mối quan hệ: 𝑆𝑆𝑇=𝑆𝑆𝑅+𝑆𝑆𝐸
Hệ số xác định 𝑅2
𝑅2=𝑆𝑆𝑅
𝑆𝑆𝑇.100%=(1−𝑆𝑆𝐸
𝑆𝑆𝑇).100%=𝑟𝑥𝑦
2.100%
Hệ số 𝑅2giải thích trong 100% sự biến động của Y so với
trung bình của nó thì có bao nhiêu % là do biến X gây ra.
7.Tìm khoảng tin cậy cho các hệ số 𝟎,𝟏của đườ ồ
quy tuyến tính.
a/Khoảng tin cậy cho tung độ gốc 0 (hệ
số chặn) là (0−𝜀0;0+𝜀0)
Với
𝜀0=𝑡𝛼/2
𝑛−2√𝑥2
𝑆𝑥𝑥.𝑆𝑆𝐸
𝑛−2
=𝑡𝛼
2
𝑛−2.1
𝑠𝑥
√𝑥2
𝑆𝑆𝐸
𝑛(𝑛−2)
Cách tính:
• 𝑥2
=1
𝑛∑𝑥𝑖2𝑛
𝑖=1
• 𝑠𝑥
2=1
𝑛∑ (𝑥𝑖−𝑥)2
𝑛
𝑖=1 =𝑥2
−(𝑥)2
• 𝑡𝛼/2
𝑛−2 tra bảng Student hàng n-2 cột 𝛼/2
b/Khoảng tin cậy cho hệ số góc 1 là
(1−𝜀1;1+𝜀1)
Với
𝜀1=𝑡𝛼/2
𝑛−2√𝑆𝑆𝐸
(𝑛−2)𝑆𝑥𝑥
=𝑡𝛼
2
𝑛−2.1
𝑠𝑥
√𝑆𝑆𝐸
𝑛(𝑛−2)
Cách Casio:
Casio 570, Vinacal
Casio 580
Step1: Mở tần số: Shift → Mode → ∇→ 4→ ON
Step2: Nhập bảng: Mode → Thống kê (3) → 2
Nhập giá trị X và cột X , giá trị Y và cột Y và nhập xác
suất của biến đó vào cột Freq, xong rôi ấn AC
Step 3: Xem các đặc trưng của mẫu: Shift →1→ 4
Step 4: Hồi quy tuyến tính: Xem hồi quy: AC→5
Tính giá trị y dự đoán tại x=a
AC→5 (ℎồ𝑖 𝑞𝑢𝑦)
Nhập a𝑦 rồi bấm bằng
Step 1: Mở tần số
Shift → Menu → ∇→ 3→ 1
Step2: Nhập bảng: Menu → Thống kê(6) →2(a+bx)
Nhập giá trị X và cột X, giá trị Y và cột Y và nhập xác suất của biến đó vào cột Freq,
xong rôi ấn AC
Step 3:Xem các đặc trưng của mẫu: Option (OPTN) →∇→ 2
Step 4: Hồi quy tuyến tính: Xem hồi quy: Option
(OPTN) →∇→ 3
Tính giá trị y dự đoán tại x=a
Option (OPTN) →∇→ ∇→4→5 (ℎồ𝑖 𝑞𝑢𝑦)
Nhập a𝑦 rồi bấm bằng
Ví dụ sai số chuẩn trong bài toán kiểm định tỉ lệ 1 mẫu. Tương tự cho các công thức khác
HCMUT-CNCP THỐNG KÊ NÂNG CAO HK242
Hiệu 2 tỉ lệ 2 mẫu 𝒑𝟏−𝒑𝟐
a/Phân phối hiệu tỉ lệ 2 mẫu 𝑝1−𝑝2
Sai số chuẩn trong bài toán kiểm định chính là mẫu số trong công thức tính 𝑻𝒕𝒆𝒔𝒕,𝒁𝒕𝒆𝒔𝒕