Đáp án đề thi cuối học kỳ II năm học 2018-2019 môn Điều khiển tự động - ĐH Sư phạm Kỹ thuật

Chia sẻ: Đinh Y | Ngày: | Loại File: PDF | Số trang:6

Thêm vào BST

Báo xấu

88
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mời các bạn cùng tham khảo đáp án đề thi cuối học kỳ II năm học 2018-2019 môn Điều khiển tự động dưới đây để có thêm tài liệu tham khảo cũng như củng cố kiến thức trước khi bước vào kì thi. Cùng tham khảo và giải đề thi để ôn tập kiến thức và làm quen với cấu trúc đề thi.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đáp án đề thi cuối học kỳ II năm học 2018-2019 môn Điều khiển tự động - ĐH Sư phạm Kỹ thuật

TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT ĐỀ THI CUỐI KỲ HỌC KỲ 2 NĂM HỌC THÀNH PHỐ HỒ CHÍ MINH 2018-2019 KHOA CƠ KHÍ CHẾ TẠO MÁY Môn: Điều Khiển Tự Động BỘ MÔN CƠ ĐIỆN TỬ Mã môn học: AUCO330329 ------------------------- Đề số: 01 Đề thi có 2 trang. Thời gian: 90 phút. Sinh viên được phép sử dụng tài liệu và máy vi tính nhưng không được kết nối wifi, 3G, Internet, và không sử dụng điện thoai di động. 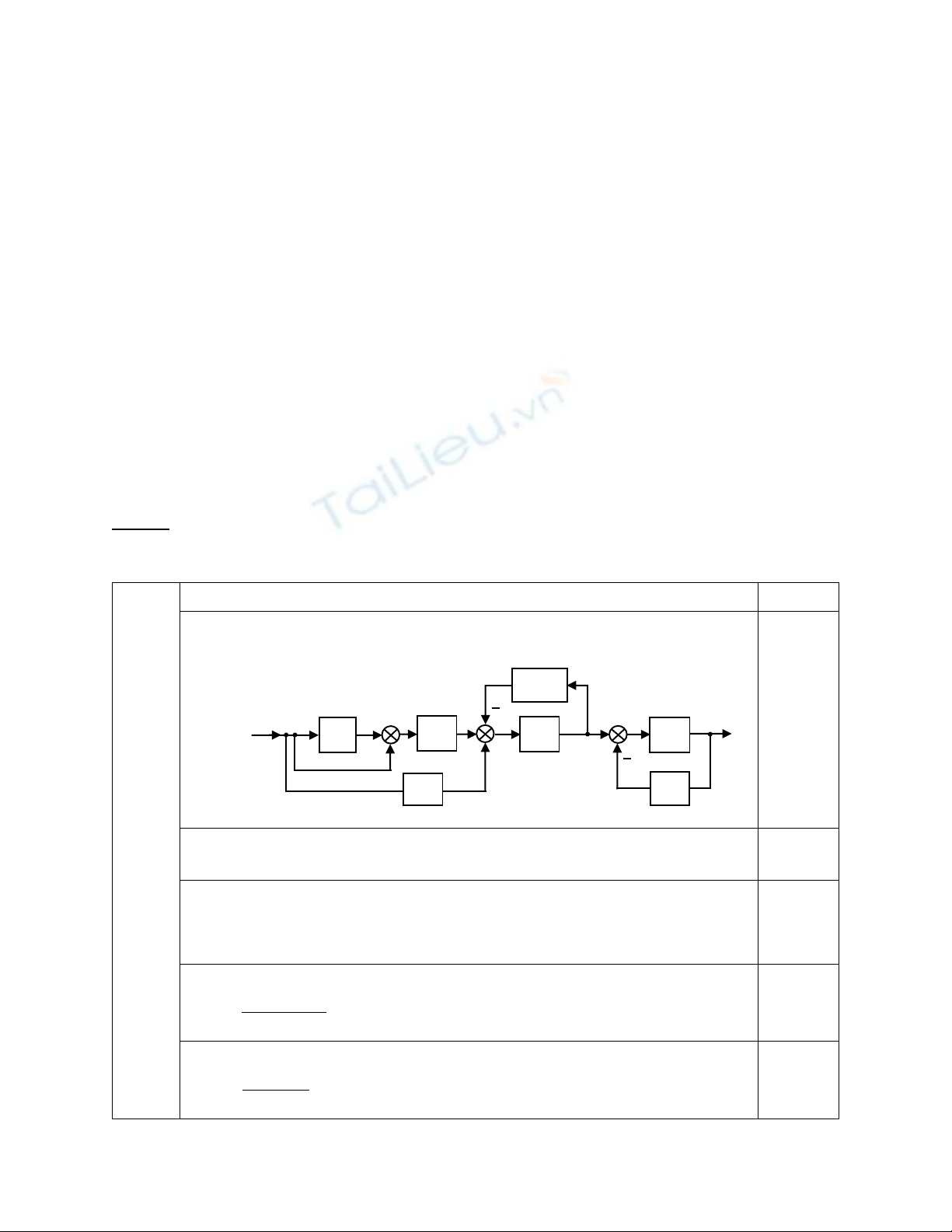ĐÁP ÁN Môn Thi: Điều Khiển Tự Động Câu 1: Đáp án Điểm Sơ đồ tương đương: - Biến đổi đúng quy tắc đại số sơ đồ khối (0,25đ) 0,25 - Có đóng khung các khối (0,25đ) 0,25 G2H1 R Y G1 G2 G3 G4 G5 H2 Xét hệ G1 // mạch đơn vị : 0,25 Gtd1  G1  1 Xét hệ (Gtd1 nối tiếp G2) // G5 : 0,25 G td2  G td1G 2  G 5 G td2  G1G 2  G 2  G 5 0,25 Xét hệ hồi tiếp âm đơn vị G3 – G2H1: 0,25 G3 G td3  1  G 3G 2 H1 Xét hệ hồi tiếp G4 – H2: 0,25 G4 G td4  1  G 4H2
Hàm truyền của hệ thống cũng là hàm truyền hệ nối tiếp: 0,25 Gtd  Gtd2 .Gtd3.Gtd4  G3   G4   G td  (G1G 2  G 2  G 5 ).  .   1  G 2 3 1   1  G 4H2  G H 0,25 G1G 2G3G 4  G 2G3G 4  G5G3G 4  G td  1  G 2G3H1  G 4H2  G 2G3H1G 4H 2 0,25 Sinh viên có thể có các cách giải khác nhau và cũng sẽ được tính điểm theo từng bước làm đúng như đáp án trên CÂU 2 Đáp án Điểm (2,5 a Giả sử tín hiệu nhiễu d(t)=0, tìm hàm truyền giữa ngõ ra y(t) và tín điểm) hiệu vào r(t). YR ( s ) Gc ( s)G ( s ) 0,25   R( s ) 1  Gc ( s)G ( s )  2  s  5    YR ( s )  s    s  1 s  6   0,5  R( s)  2  s  1  5     s    s  1 s  6   0,25 YR ( s )  2  2  5s  R( s) s  12s  8 b Giả sử tín hiệu ngõ vào r(t)=0, tìm hàm truyền giữa ngõ ra y(t) và tín hiệu nhiễu d(t) 0,25 0,5
YD ( s) G(s)   D( s) 1  Gc ( s)G( s) 0,25  s    YR ( s)   s  1 s  6    R( s )  2  s  1  5      s    s  1 s  6   YR ( s) s  2 R( s) s  12s  8 c Giả sử tín hiệu ngõ vào r(t)=1(t) và d(t)=0,05 x 1(t), tìm tín hiệu ra y(t).   2  5s   1  s  0, 05 Y ( S )  YR ( s )  YD ( s )   2   2   s  12s  8  s  s  12s  8  s Y (S )   2  5s    0, 05    2  5, 05s  0,25  2  s  s 2  12s  8   s  12s  8  s  s 2  12s  8  0,25 Câu 3 (2,50 điểm) Đáp án Điểm A Tìm hàm truyền hệ thống kín Hàm truyền hệ thống kín G(s) K G k (s)   3 1  G(s) s  15s  50s  K 2 0,25 Phương trình đặc tính của hệ thống s3  15s2  50s  K  0 Vẽ quỹ đạo nghiệm số: G(s) có ba cực là p1 = 0 ; p2 =  5; p2 =  10 và không có zero. 0,25  Quỹ đạo nghiệm hệ kín gồm ba nhánh xuất phát từ các cực khi K=0. 0,25 Khi K, ba nhánh tiến tới  theo các tiệm cận xác định bởi:
Góc giữa các tiệm cận và trục thực (2i  1) (2i  1)  5 0,25 i     ;; nm 30 3 3 Giao điểm giữa các tiệm cận và trục thực có hoành độ: Ro   poles   zeros  (0  5  10)  0  5 nm 30 0,25 QĐN đối xứng qua trục thực Xác định điểm tách của QĐN Viết lại phương trình đặc tính :  s3  15s2  50s  K  0  K   s3  15s 2  50s  0,25 dK Từ phương trình đặc tính suy ra:  (3s 2  30s  50) ds dK Do đó: 0  (3s2  30s  50)  0 ds 0,25 Giải ra ta được hai nghiệm s1 =  7.87 và s2 =  2.11 Chỉ có nghiệm s2 phù hợp là điểm tách vì thoả điều kiện tổng số cực và zero bên phải nó là một số lẻ. 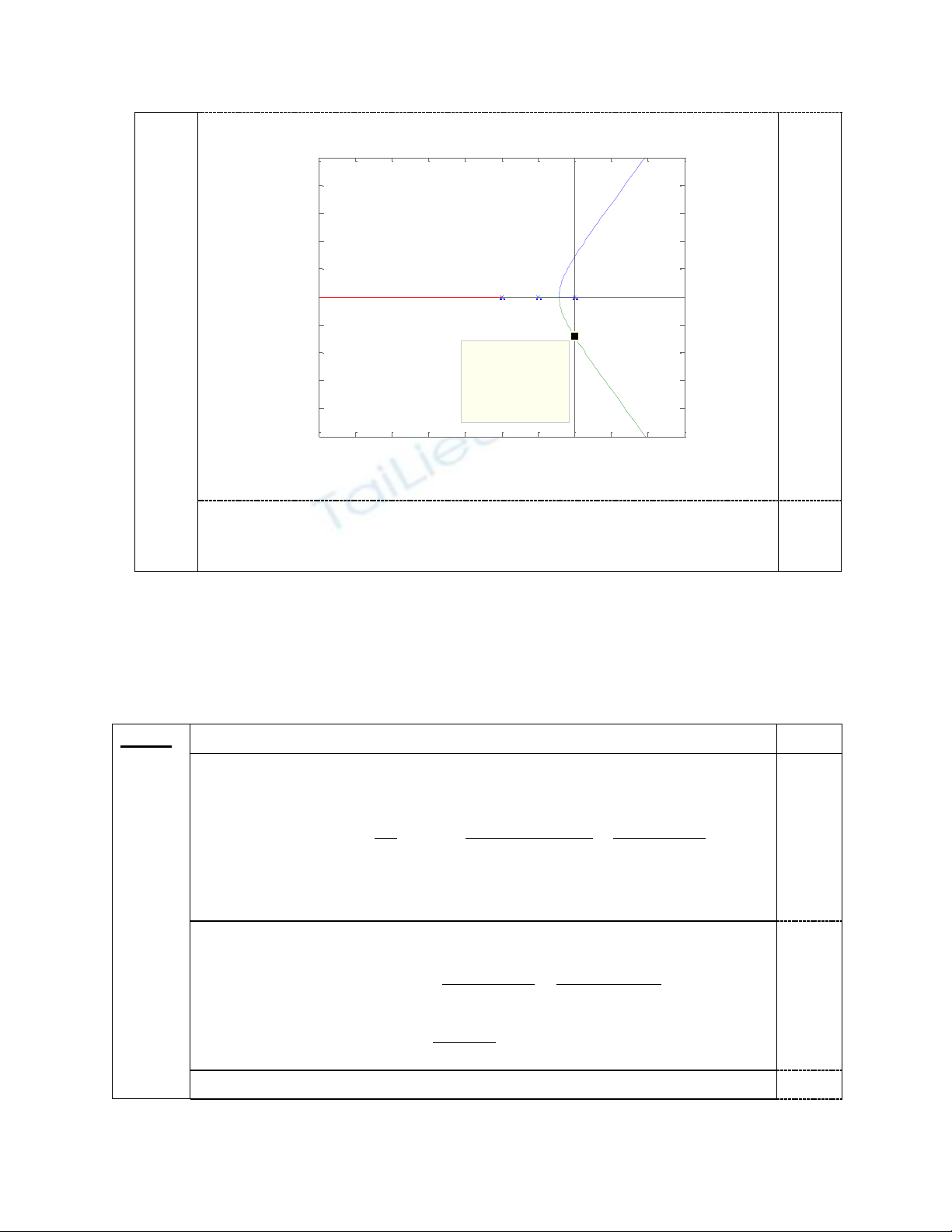Giao điểm của QĐN với trục ảo: Thay s = j vào phương trình đặc tính ta được:  j3  152  50 j  K  0 15  K  0 2    50  0 3   0; K  0     50 ; K  750 0,25 Vậy các giao điểm cần tìm là s   j 50   j7, 07 Đồ thị của QĐN: - Vẽ đúng biên dạng quỹ đạo nghiệm số 0,25 - Đặt đúng các giá trị trên quỹ đạo nghiệm số
Root Locus 25 20 15 Imaginary Axis (seconds-1) 10 5 0 -5 -10 System: ht Gain: 751 Pole: 0.00179 - 7.07i -15 Damping: -0.000253 Overshoot (%): 100 -20 Frequency (rad/s): 7.07 -25 -35 -30 -25 -20 -15 -10 -5 0 5 10 15 Real Axis (seconds -1) 0  K  750 Hệ thống không ổn định 0,25 K  750 Hệ thống ở biên giới ổn định K  750 Hệ thống ổn định Câu 4 Đáp án Điểm (2,5 điểm) a) Tìm hàm truyền của hệ thống Hàm truyền bộ PID: KI K s 2  K Ps  K I s 2  12s  35 G PID (s)  K P   K Ds  D  s s s 0,25 Hàm truyền mạch chính:  s 2  12s  35   6  G h (s)  G PID (s).G(s)        s  5  s  17   0,25  s 6(s  7) G h (s)  G PID (s).G(s)  s(s  17) Hàm truyền kín của hệ thống :
Y(s) G PID (s).G(s) 6(s  7) 0,25 G k (s)    2 R(s) 1  G PID (s).G(s) s  23s  42 b) Tìm đáp ứng quá độ và sai số xác lập e() của hệ thống. Ảnh Laplace của đáp ứng quá độ: G k (s) 6(s  7) Y(s)  R(s)G k (s)   0,25 s  s s  23s  42 2  Mẫu số của Y(s) có 3 nghiệm s= 0 ; s= -2 ; s= -21 6(s  7) A A A3 0,25 Y(s)   1 2  s(s  2)(s  21) s s  2 s  21 6(s  7) 0,25 A1  lim sY(s)  lim 2 1 s0 s0 s  23s  42 6(s  7) 15 A 2  lim (s  2)Y(s)   lim  0,25 s2 s2 s(s  21) 19 6(s  7) 4 0,25 A3  lim (s  21)Y(s)   lim  s21 s21 s(s  2) 19 1 15 12  Y(s)    s 19(s  2) 57(s  21) 0,25 15 4  Đáp ứng quá độ: y(t)  L [Y(s)]  1  e2 t  e21t 1 19 19 Sai số xác lập: e()  r()  y()  1  lim y(t)  1 1  0 0,25 t 