TR NG THCS&THPT TÀ NUNGƯỜ Đ C NG ÔN T P H C KÌ IỀ ƯƠ Ậ Ọ
T TOÁN-LÍ-TIN Ổ MÔN TOÁN L P 9 - NĂM H C 2016- 2017Ớ Ọ
I. LÝ THUY TẾ: C n ôn l i các ki n th c sau:ầ ạ ế ứ
A. ĐI SẠ Ố:
Ch ng I ươ CĂN B C HAI - CĂN B C BAẬ Ậ
+ Đnh nghĩa căn b c hai c a m t s a không âmị ậ ủ ộ ố
+ Nêu đi u ki n đ x là căn b c hai s h c c a s a không âm.ề ệ ể ậ ố ọ ủ ố
+. Đi u ki n xác đnh c a ề ệ ị ủ
483512
+ N m đc ắ ượ h ng đng th c: ằ ẳ ứ
AA
2
+N m đc các quy t c và công th c v ắ ượ ắ ứ ề liên h gi a phép nhân và phép khai ph ng, liên h gi a phép chia ệ ữ ươ ệ ữ
và phép khai ph ngươ
+ N m đc các phép bi n đi đn gi n bi u th c ch a căn b c hai(ắ ượ ế ổ ơ ả ể ứ ứ ậ đa th a s ra ngoài căn, ,đa th a s ư ừ ố ư ừ ố
vào trong căn, kh căn th c m u và ử ứ ở ẫ tr c căn th c m u)ụ ứ ở ẫ
+Đnh ngh a căn b c baị ỉ ậ
Ch ng II HÀM S - HÀM S B C NH Tươ Ố Ố Ậ Ấ
- Khái ni m hàm s ệ ố
- Đnh nghĩa, tính ch t và đ th c a hàm s b c nh tị ấ ồ ị ủ ố ậ ấ
- Đi u ki n đ hai đng th ng: y = ax + b; y = aề ệ ể ườ ẳ ,x + b, song song, trùng nhau, c t nhau, c t nhau t i 1 đi m ắ ắ ạ ể
thu c tr c tung.ộ ụ
-Bi t xác đnh và bi t cách tính góc t o b i ế ị ế ạ ở đng th ng v i tr c Oxườ ẳ ớ ụ
Ch ng III: H 2 PT B C NH T 2 Nươ Ệ Ậ Ấ Ẩ
-Khái ni m pt b c nh t 2 n, Khi nào c p s (ệ ậ ấ ẩ ặ ố
0, 0
x y
) đc g i là 1 nghi m c a pt? PT b c nh t 2 n có th ượ ọ ệ ủ ậ ấ ẩ ể
có bao nhiêu nghi m?ệ
-Khái ni m v h pt b c nh t 2 nệ ề ệ ậ ấ ẩ
-Th nào là h 2 PT t ng đngế ệ ươ ươ
-Khi nào h pt b c nh t 2 n có m t nghi m duy nh t, có vô s nghi m, vô nghi m?ệ ậ ấ ẩ ộ ệ ấ ố ệ ệ
-Nêu cách gi i h pt b ng ph ng pháp th và ph ng pháp c ng đi s .ả ệ ằ ươ ế ươ ộ ạ ố
B. HÌNH H CỌ:
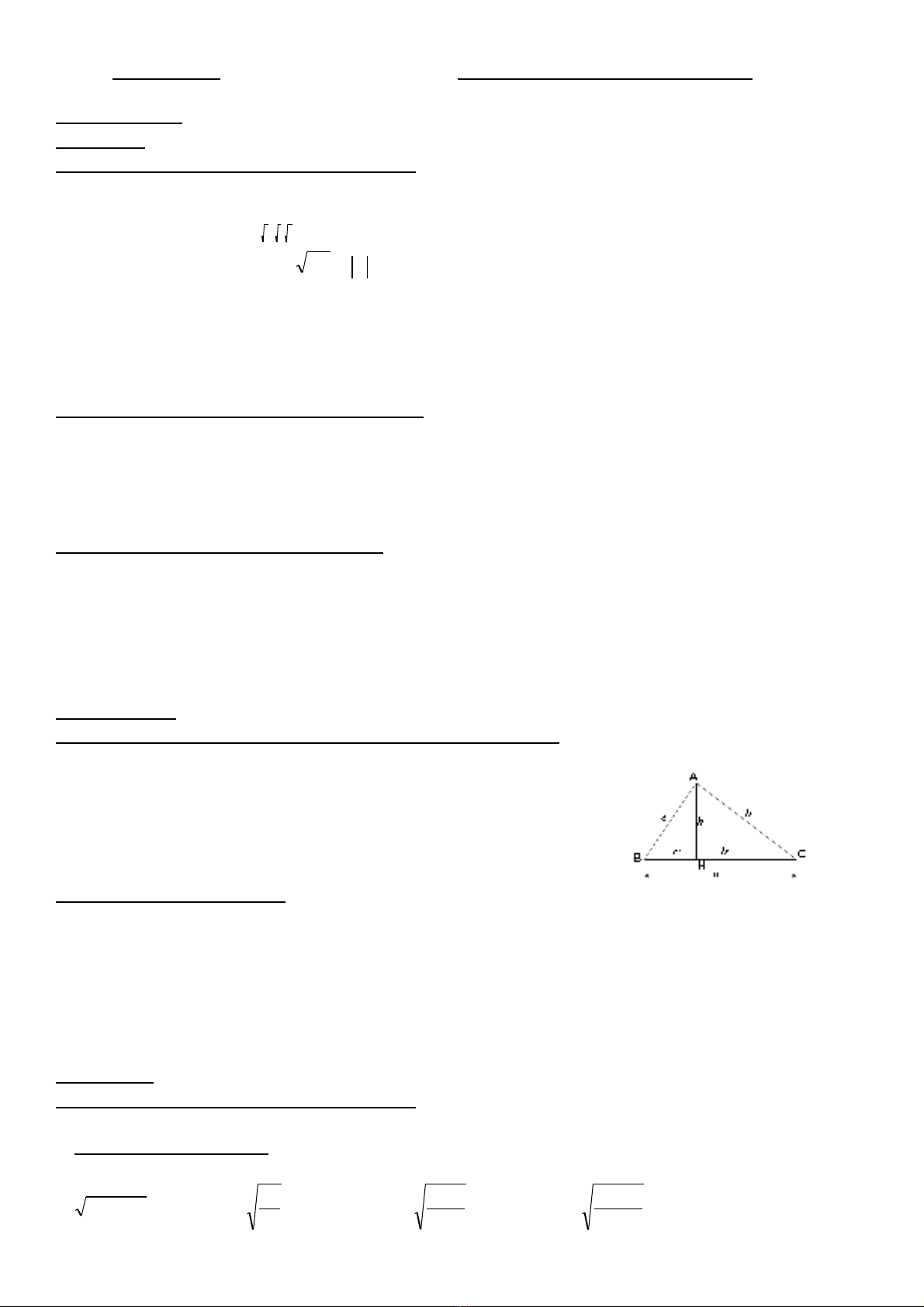
Ch ng I. H TH C L NG TRONG TAM GIÁC VUÔNGươ Ệ Ứ ƯỢ
Cho hình v : ẽ
+Vi t các h th c gi a c nh góc vuông và hình chi u c a nó lên c nh huy n.ế ệ ứ ữ ạ ế ủ ạ ề
+Vi t các h th c liên quan t i đng cao trong tam giác vuông.ế ệ ứ ớ ườ
+ Vi t t s l ng giác c a góc B r i suy ra t s l ng giác c a góc Cế ỉ ố ượ ủ ố ỉ ố ượ ủ
+ Vi t các h th c gi a c nh và góc trong tam giác vuôngế ệ ứ ữ ạ
+Vi t 4 công th c b sung v t s l ng giác.ế ứ ổ ề ỉ ố ượ
Ch ng II. ĐNG TRÒNươ ƯỜ
+M t đng tròn xác đnh khi bi t nh ng y u t nào?ộ ườ ị ế ữ ế ố
+Phát bi u đnh lí v quan h vuông góc gi a đng kính và dây cung.ể ị ề ệ ữ ườ
+Phát bi u đnh lí v m i liên h gi a dây và kho ng cách t tâm đn dây.ể ị ề ố ệ ữ ả ừ ế
+Nêu các v trí t ng đi gi a đng tròn cùng các h th c t ng ng.ị ươ ố ữ ườ ệ ứ ươ ứ
+Đnh nghĩa ti p tuy n c a đng tròn, tính ch t v ti p tuy n c a đng tròn.ị ế ế ủ ườ ấ ề ế ế ủ ườ
+Nêu các d u hi u nh n bi t ti p tuy n c a đng trònấ ệ ậ ế ế ế ủ ườ
+Nêu tính ch t c a 2 ti p tuy n c t nhau.ấ ủ ế ế ắ
B. BÀI T PẬ
Ch ng I ươ CĂN B C HAI - CĂN B C BAẬ Ậ
Tìm đi u ki n xác đnh:ề ệ ị V i giá tr nào c a x thì các bi u th c sau đây xác đnh:ớ ị ủ ể ứ ị
1)
32 x
2)
2
2
x
3)
3
4
x
4)
6
5
2
x
5)
43 x
6)
2
1x
7)
x21
3
8)
Rút g n bi u th c ọ ể ứ
Bài 1
1)
483512
2)
4532055
3)
18584322
4)
485274123
5)
277512
6)
16227182
7)
54452203
8)
222)22(
9)
15
1
15
1
10)
25
1
25
1
11)
234
2
234
2
12)
21
22
13)
877)714228(
14)
286)2314( 2
15)
120)56( 2
16)
24362)2332( 2
17)
22 )32()21(
18)
22 )13()23(
19)
22 )25()35(
20)
)319)(319(
21)
)2()12(4 2 xxx
22)
57
57
57
57
23)
)2()44(2
222
yxyxyxyx
Bài 2
1)
22 2323
2)
22
3232
3)
2 2
( 5 3) ( 5 3)− + +
4)
1528
-
1528
5)
625
+
1528
6)
83
5
223
5
324324
Bài 3: Tr c căn th c m u: ụ ứ ở ẫ
1)
2
5 1−
; 2)
1
3 3 2 2−
; 3)
3 7
3 7
−
+
; 4)
1
2 3 5+ +
; 5)
1 3
3 1
+
−
Gi iả ph ng trình:ươ
1)
512 x
2)
35 x
3)
21)1(9 x
4)
0502 x
5)
0123
2
x
6)
9)3( 2x
7)
6144 2 xx
8)
3)12( 2x
9)
64
2
x
10)
06)1(4 2 x
11)
21
3x
12)
223
3 x
CÁC BÀI TOÁN RÚT G NỌ :
Bài 1. Cho bi u th c : P = ể ứ
4 4 4
2 2
a a a
a a
+ + −
+
+ −
( V i a ớ
0 ; a
4 )
a) Rút g n bi u th c P;ọ ể ứ
b)Tìm giá tr c a a sao cho P = a + 1.ị ủ
Bài 2: Cho bi u th c A =ể ứ
1 2
1 1
x x x x
x x
+ − +
+
− +
a)Đt đi u ki n đ bi u th c A có nghĩa;ặ ề ệ ể ể ứ
b)Rút g n bi u th c A;ọ ể ứ
c)V i giá tr nào c a x thì A< -1.ớ ị ủ
Bài 3: Cho bi u th c A =ể ứ
(1 )(1 )
1 1
x x x x
x x
+ −
+ −
+ −
( V i ớ
0; 1x x
)
a) Rút g n A;ọ
b) Tìm x đ A = - 1.ể
Bài 4 : Cho bi u th c : B = ể ứ
x
x
xx
1
22
1
22
1
a) Tìm TXĐ r i rút g n bi u th c B;ồ ọ ể ứ
b) Tính giá tr c a B v i x =3;ị ủ ớ
c) Tìm giá tr c a x đ ị ủ ể
2
1
A
.
Ch ng II HÀM S - HÀM S B C NH Tươ Ố Ố Ậ Ấ
Bài 1:Cho hàm s : y= (m+6)x-7ố
a. V i giá tr nào c a m thì hàm s trên là hàm s b c nh t.ớ ị ủ ố ố ậ ấ
b. V i giá tr nào c a m thì hàm s trên là hàm s đng bi n, ngh ch bi n.ớ ị ủ ố ố ồ ế ị ế
Bài 2: Cho đng th ng: y= (1-m) x+m-2 có đ th là (d)ườ ẳ ồ ị
a.V i giá tr nào c a m thì hàm s trên là hàm s b c nh t.ớ ị ủ ố ố ậ ấ
b. V i giá tr nào c a m thì hàm s trên là hàm s đng bi n, ngh ch bi n.ớ ị ủ ố ố ồ ế ị ế
c.V i giá tr nào c a m thì (d) đi qua đi m A(1;2)ớ ị ủ ể
d.V i giá tr nào c a m thì (d) c t tr c tung t i đi m có tung đ b ng 3.ớ ị ủ ắ ụ ạ ể ộ ằ
e.V i giá tr nào c a m thì (d) c t tr c hoành t i đi m có hoành đ b ng -2ớ ị ủ ắ ụ ạ ể ộ ằ
f.V i giá tr nào c a m thì (d) t o v i tr c Ox m t góc nh n, góc tù.ớ ị ủ ạ ớ ụ ộ ọ
Bài 3: Cho hai đng th ng (dườ ẳ 1): y = ( 2 + m )x + 1 và (d2): y = ( 1 + 2m)x + 2
1) Tìm m đ (dể1) và (d2) c t nhau .ắ
2) V i m = – 1 , v (dớ ẽ 1) và (d2) trên cùng m t ph ng t a đ Oxy r i tìm t a đ giao đi m c a hai đng ặ ẳ ọ ộ ồ ọ ộ ể ủ ườ
th ng (dẳ1) và (d2) b ng phép tính.ằ
Bài 4: V i giá tr nào c a m thì hai đng th ng y = 2x + 3+m và y = 3x + 5- m c t nhau t i m t đi m trên ớ ị ủ ườ ẳ ắ ạ ộ ể
tr c tungụ
Bài 5: Cho hàm s b c nh t y = (1- 3m)x + m + 3 đi qua N(1;-1) , hàm s đng bi n hay ngh ch bi n ? Vì sao?ố ậ ấ ố ồ ế ị ế
Bài 6: Cho hai đng th ng y = mx – 2 ;(mườ ẳ
)0
và y = (2 - m)x + 4 ;
)2( m
. Tìm đi u ki n c a m đ hai ề ệ ủ ể
đng th ng trên:a)Song song; b)C t nhau .ườ ẳ ắ
Bài 7: Vi t ph ng trình đng th ng (d) bi t (d) song song v i (d’): y = ế ươ ườ ẳ ế ớ
x
2
1
và c t tr c hoành t i đi m có ắ ụ ạ ể
hoành đ b ng 10.ộ ằ
Bài 8: Vi t ph ng trình đng th ng (d), bi t (d) song song v i (d’) : y = - 2x và đi qua đi m A(2;7).ế ươ ườ ẳ ế ớ ể
Bài 9: Vi t ph ng trình đng th ng đi qua hai đi m A(2; - 2) và B(-1;3).ế ươ ườ ẳ ể
Bài 10: Cho hai đng th ng : (dườ ẳ 1): y =
12
2x+
và (d2): y =
2x− +
a/ V (dẽ1) và (d2) trên cùng m t h tr c t a đ Oxy.ộ ệ ụ ọ ộ
b/ G i A và B l n l t là giao đi m c a (dọ ầ ượ ể ủ 1) và (d2) v i tr c Ox , C là giao đi m c a (dớ ụ ể ủ 1) và (d2) Tính chu vi và
di n tích c a tam giác ABC (đn v trên h tr c t a đ là cm)?ệ ủ ơ ị ệ ụ ọ ộ
Bài 11: Cho các đng th ng (dườ ẳ 1) : y = 4mx - (m+5) v i mớ
0
(d2) : y = (3m2 +1) x +(m2 -9)
a; V i giá tr nào c a m thì (dớ ị ủ 1) // (d2)
b; V i giá tr nào c a m thì (dớ ị ủ 1) c t (dắ2) tìm to đ giao đi m Khi m = 2 ạ ộ ể
Bài 12: Cho hàm s : y = ax +b ố
a; Xác đnh hàm s bi t đ th c a nó song song v i y = 2x +3 và đi qua đi m A(1,-2)ị ố ế ồ ị ủ ớ ể
b; V đ th hàm s v a xác đnh r i tính đ l n góc ẽ ồ ị ố ừ ị ồ ộ ớ t o b i đng th ng trên v i tr c Ox ?ạ ở ườ ẳ ớ ụ
c; Tìm to đ giao đi m c a đng th ng trên v i đng th ng y = - 4x +3 ?ạ ộ ể ủ ườ ẳ ớ ườ ẳ
d.Tìm giá tr c a m đ đng th ng trên song song v i đng th ng y = (2m-3)x +2ị ủ ể ườ ẳ ớ ườ ẳ
Bài 13: Cho các PT: a. 3x-2y=6 ; b . 5x+0y=5 ; c.0x=4y=8. Tìm công th c nghi m t ng quát c a m i pt trênứ ệ ổ ủ ỡ
Bài 14: Trong các tr ng h p sau , 2 h pt nào là t ng đng v i nhau:ườ ợ ệ ươ ươ ớ
a.
{
3 6 7
2 2
x y
x y
+ =
+ =
và
{
4 8 4
2 3
x y
x y
− − =
− =
b.
{
1,5 0,5
2 3 1
x y
x y
− − =−
+ =
và
{
3 8
2
x y
y
+ =−
=
Bài 15: Gi i các h pt sau b ng ph ng pháp th : ả ệ ằ ươ ế
{
4 5 3
3 5
x y
x y
+ =
− =
{
7 2 1
3 6
x y
x y
− =
+ =
{
1,3 4,2 12
0,5 2,5 5,5
x y
x y
+ =
+ =
{
2 3 3 5 21
5 5
x y
x y
+ =
− =
Bài 16: Gi i các h pt sau b ng pp c ng đi s : ả ệ ằ ộ ạ ố
{
10 11 31
2 11 7
x y
x y
+ =
− =
{
10 9 8
15 21 0,5
x y
x y
− =
+ =
{
3,3 4,2 1
9 14 4
x y
x y
+ =
+ =
{
12 13 1
8 7 5
x y
x y
+ =
− =
B. HÌNH H CỌ:
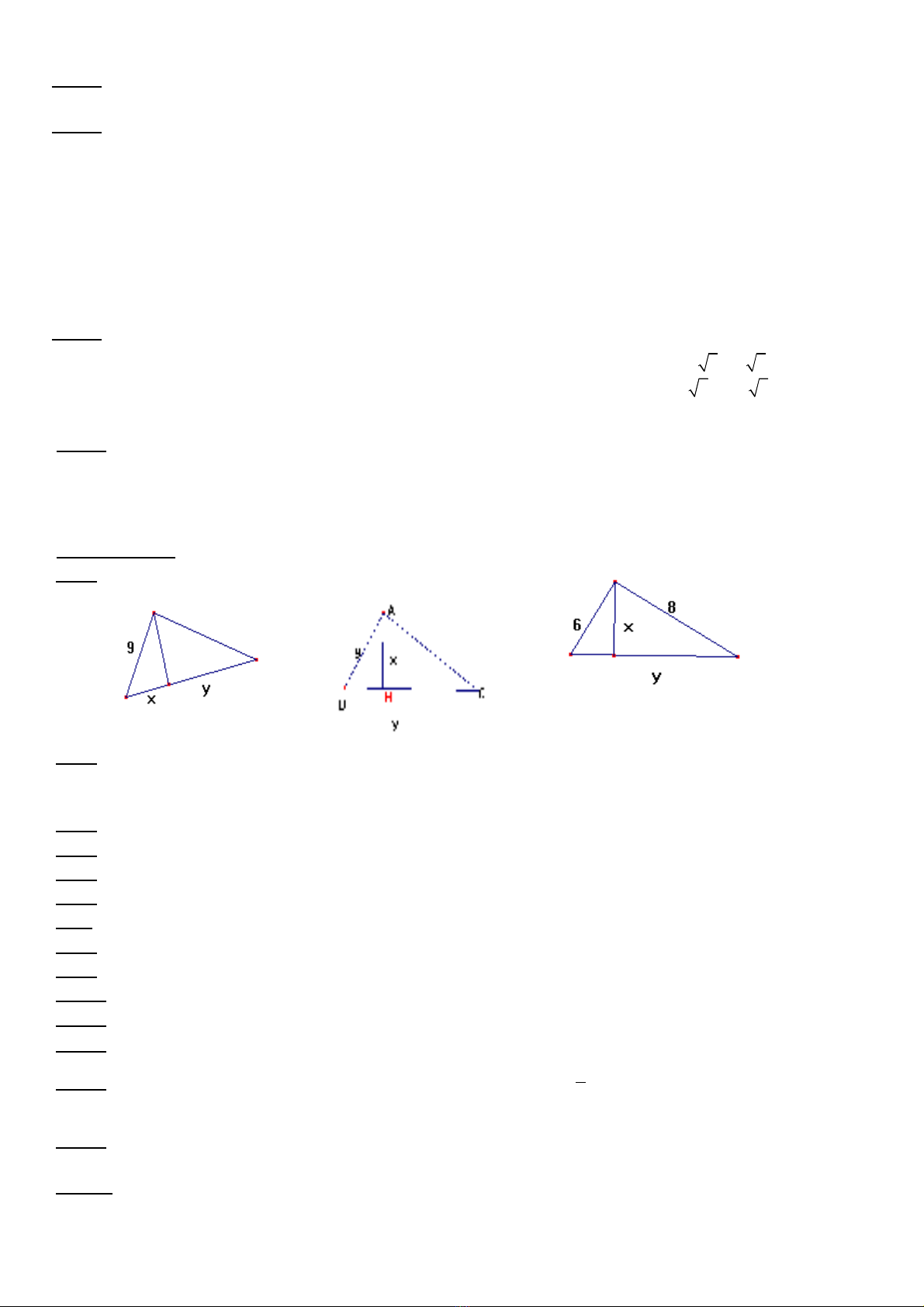
Bài 1: Tìm x, y trong các hình v sau: ẽ
.
Bài 2: Caïnh huyeàn cuûa moät tam giaùc vuoâng laø 10cm, caùc caïnh goùc vuoâng tæ
leä vôùi 4 vaø 3 . Tính ñoä daøi hình chieáu cuûa moãi caïnh goùc vuoâng leân caïnh
huyeàn
Bài 3: Cho tam giác ABC vuông t i A có b = 4, bạ’ = 3.2. Gi i tam giác ABC?ả
Bài 4: Cho tam giác ABC vuông t i A có AH = 4.8, BC =10. Gi i tam giác ABC?ạ ả
Bài 5: Cho tam giác ABC vuông t i A có h = 4, cạ’ = 3. Gi i tam giác ABC?ả
Bài 6: Cho tam giác ABC vuông t i A có b = 12, a = 20. Gi i tam giác ABC?ạ ả
Bài7: Chotam giác ABC vuông t i A có h = 4, c = 5. Gi i tam giác ABC?ạ ả
Bài 8: Cho tam giác ABC vuông có A = 900, b = 5, B = 400. Gi i tam giác ABC?ả
Bài 9: Cho tam giác ABC vuông t i A có a = 15, B = 60ạ0. Gi i tam giác ABC?ả
Bài 10:Cho tam giác ABC vuông t i A có AH = 3, C = 40ạ0. Gi i tam giác ABC?ả
Bài 11: Cho tam giác ABC vuông t i A có cạ’ = 4, B = 550. Gi i tam giác ABC?ả
Bài 12: Chotam giác ABC vuông t i A, có trung tuy n ng v i c nh huy n mạ ế ứ ớ ạ ề
a
= 5, h = 4. Gi i tam giác ABC?ả
Bài 13: .Cho tam giaùc ABC vuoâng taïi A. Bieát sin B=
1
5
. Tính TSLG coøn laïi cuûa
B( khoâng tính soá ño goùc B).
Bài 14:Cho tam giaùc ABC vuoâng taïi A. Vieát TSLG cuûa B. Töø ñoù suy ra TSLG cuûa C
bieát AB=9cm, BC=15 cm.
Bài 15:Khoâng duøng baûng soá, maùy tính, Saép xeáp caùc TSLG sau theo thöù töï taêng
daàn:
a. Sin 400; cos 280; sin 650; cos 880;
b. Tg 650 ; cotg 420; tg 760; cotg 27 0.