Trường THPT Lê Thánh Tông
- 1 -
Soạn ngày 30 / 11 / 2011 KIỂM TRA HỌC KỲ I -11NC . NĂM HỌC : 2011-2012
. . . . . . . . . . . . . . .
MA TRẬN MỤC TIÊU GIÁO DỤC VÀ MỨC ĐỘ NHẬN THỨC
Tổng điểm
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan
trọng % Trọng số
(mức độ) Theo
ma trận
Thang
10
cơ bản 19 1 19 1
quy về pt bậc hai 7 3 21 1
PT lượng giác
lượng giác bậc 1 đv sinx,cosx 10 2 20 1
Ảnh qua phép dời hình 19 1 19 1
Ảnh qua phép vị tự 5 2 10 0,5
Bài toán chọn,xác suất 10 2 20 1
Nhị thức Niutơn 7 3 21 1
Giải phương trình chứa kk
nnn
P,A ,C 5 4 20 1
Giải phương trình LG khác 5 4 20 1
Giao tuyến 10 2 20 1
Tính chất song song 3 3 9 0,5
Tổng 100% 27 199 10
MA TRẬN ĐỀ . KIỂM TRA HỌC KỲ I -11NC . NĂM HỌC : 2011-2012
Mức độ nhận thức - Hình thức câu hỏi
1 2 3 4
Chủ đề hoặc
mạch kiến thức, kĩ năng TL TL TL TL
Tổng
điểm
cơ bản Câu 1.1
1
1
quy về pt bậc hai Câu 1.2.
1 1
PT lượng giác
lượng giác bậc 1
đv sinx,cosx
Câu 1.3
1
1
Ảnh qua phép dời hình Câu 2
1
1
Ảnh qua phép vị tự Câu .3.
0,5
0,5
Bài toán chọn,xác suất Câu 4
1
1
Nhị thức Niutơn Câu 5
1
1
Giải phương trình chứa kk
nnn
P,A ,C Câu 6
1
1
Giải phương trình LG khác Câu 7
1
1
Tính chất song song Câu 8. a
0,5
0,5
Giao tuyến Câu 8.b
1
1
Tổng điểm 242 210
WWW.ToanCapBa.Net
Trường THPT Lê Thánh Tông
- 2 -
ĐỀ KIỂM TRA HỌC KỲ I -11NC . NĂM HỌC : 2011-2012
Câu 1 (3,0 điểm). Giải các phương trình sau :
a ) 3tan(x 15 ) 3
b ) 2
3cos x 2sinx 2 0
c) 31cos2x sin2x
Câu 2 (1,0 điểm). Cho đường thẳng :3 4 1 0dx y. Tìm ảnh của d qua phép tịnh tiến theo (1;2)u
Câu 3 (0,50 điểm). Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x–1)2 + (y–2)2 = 16. Viết phương
trình đường tròn (C’) là ảnh của đường tròn (C) qua phép vị tự tâm O(0;0), tỉ số k = 3.
Câu 4 (1,0 điểm).
Một hộp đựng 3 quả cầu xanh và 2 quả cầu đỏ, chọn ngẫu nhiên hai quả cầu từ hộp. Tính xác suất để
lÊy ®−îc hai qu¶ cïng mμu .
Câu 5 (1,0 điểm). Tính giá trị của biểu thức 1 2 3 2011
2011 2011 2011 2011
T C C C ... C
Câu 6 (1,0 điểm). Giải phương trình ẩn n trong :
3
2n
A24
Câu 7 (1,0 điểm). Giải phương trình lượng giác 22 2
sin x cos 2x cos 3x
Câu 8 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là tâm của hình bình
hành. Gọi M là trung điểm của cạnh SB, N là điểm trên cạnh BC sao cho BN = 2CN.
a) Chứng minh OM song song với mặt phẳng (SAC).
b) Xác định giao tuyến của (SCD) và (AMN).
ĐÁP ÁN
Câu 1 (3,0 điểm).
a) 3
3tan(x 15 ) 3 tan(x 15 ) 3
 

(0,25 ®iÓm)
00
x15 30 k.180(k )
(0,5 ®iÓm)
0
x45 k.180(k )
(0,25 ®iÓm)
b) 2
pt33sinx2sinx20
2
3sin x 2 sin x 5 0 (0,25 ®iÓm)
sin x 1
5
sin x (lo¹i)
3

(0,5 ®iÓm)
sin x 1 x k2 .
2

KL : x k2 ,k
2
 (0,25 ®iÓm)
c) 131
pt cos2x sin x
222
 (0,25 ®iÓm)
cos 2x cos
33




 (0,25 ®iÓm)
2x k2
33
2x k2
33




(0,25 ®iÓm)
WWW.ToanCapBa.Net
Trường THPT Lê Thánh Tông
- 3 -
xk
3
xk


(0,25 ®iÓm)
Câu 2 (1,0 điểm).
Gọi d’ là ảnh của d qua phép tịnh tiến theo ( 1; 2)u
Lấy M(x,y)d, M’(x’,y’) d’
Khi đó: '''1
'''2
xxa x a x x x
yyb y b y y y
 





(0,25 ®iÓm)
Thay vào phương trình đường thẳng d, ta được:
3(x ' 1) 4(y ' 2) 1 0
 (0,25 ®iÓm)
3x ' 4y ' 3 8 1 0
M '(x ', y ') d ' : 3x ' 4y ' 6 0
 (0,25 ®iÓm)
Vậy ' : 3 4 6 0
dxy (0,25 ®iÓm)
Câu 3 (0,50 điểm).
(C) có tâm I(1;2),bán kính R=4
(C’) có tâm I’(3;6),bán kính R’= |k|R =12 (0,25 ®iÓm)
Pt /22
(C ) : (x 3) (y 6) 144 (0,25 ®iÓm)
Câu 4 (1,0 điểm).
Sè kÕt qu¶ cã thÓ cã lμ n( )= 2
20
C=190 (0,25 ®iÓm)
C¸ch 1. Gäi A lμ biÕn cè: “Chän ®−îc hai qu¶ kh¸c mμu ” n( A
)= 11
15 5
C.C
(0,5 ®iÓm)
P(A)= 11
15 5
2
20
C.C 15
38
C
. (0,25 ®iÓm)
C¸ch 2. Suy ra A lμ biÕn cè: “Chän ®−îc hai qu¶ cïng mμu ”
22
22 515
515
A2
20
CC 23 23 15
n( ) C C P(A) P(A) 1
38 38 38
C

Câu 5 (1,0 điểm) Xét n01 22 nn
nn n n
(1 x) C C .x C .x ... C .x (*) (0,25 ®iÓm)
Thay x =1, n = 2011 vào (*) , ta được : 2011 0 1 2 2000
2011 2011 2011 2011
(11) CCC...C (0,5 ®iÓm)
Do đó : 2011
T2 (0,25 ®iÓm)
Câu 6 (1,0 điểm) Điều kiện :







3
2n 3 n 2
n2
nn
n
(0,25 ®iÓm)
Ta có :
3
2n
A24(2n)! 24
(2n 3)!

(0,25 ®iÓm)
(2n 3)!(2n 2)(2n 1)2n 24 (2n 2)(2n 1)2n 24
(2n 3)!


(0,25 ®iÓm)

32 2
2n 3n n60 (n2)(2n n3)0 n 2 (0,25 ®iÓm)
Vậy phương trình có nghiệm n = 2 .
Câu 7 (1,0 điểm).
22 2
1 cos2x 1 cos4x 1 cos6x
sin x cos 2x cos 3x 222

 (0,25 ®iÓm)
2
(cos2x cos 4x) (cos6x 1) 0 2 cos3x cosx 2cos 3x 0 (0,25 ®iÓm)
2cos3x.(cosx cos3x) 0 2cosxcos2xcos3x 0 (0,25 ®iÓm)
WWW.ToanCapBa.Net
Trường THPT Lê Thánh Tông
- 4 -
cosx 0 kk
cos2x0xk v x v x víi k
24263
cos3x 0

  
(0,25 ®iÓm)
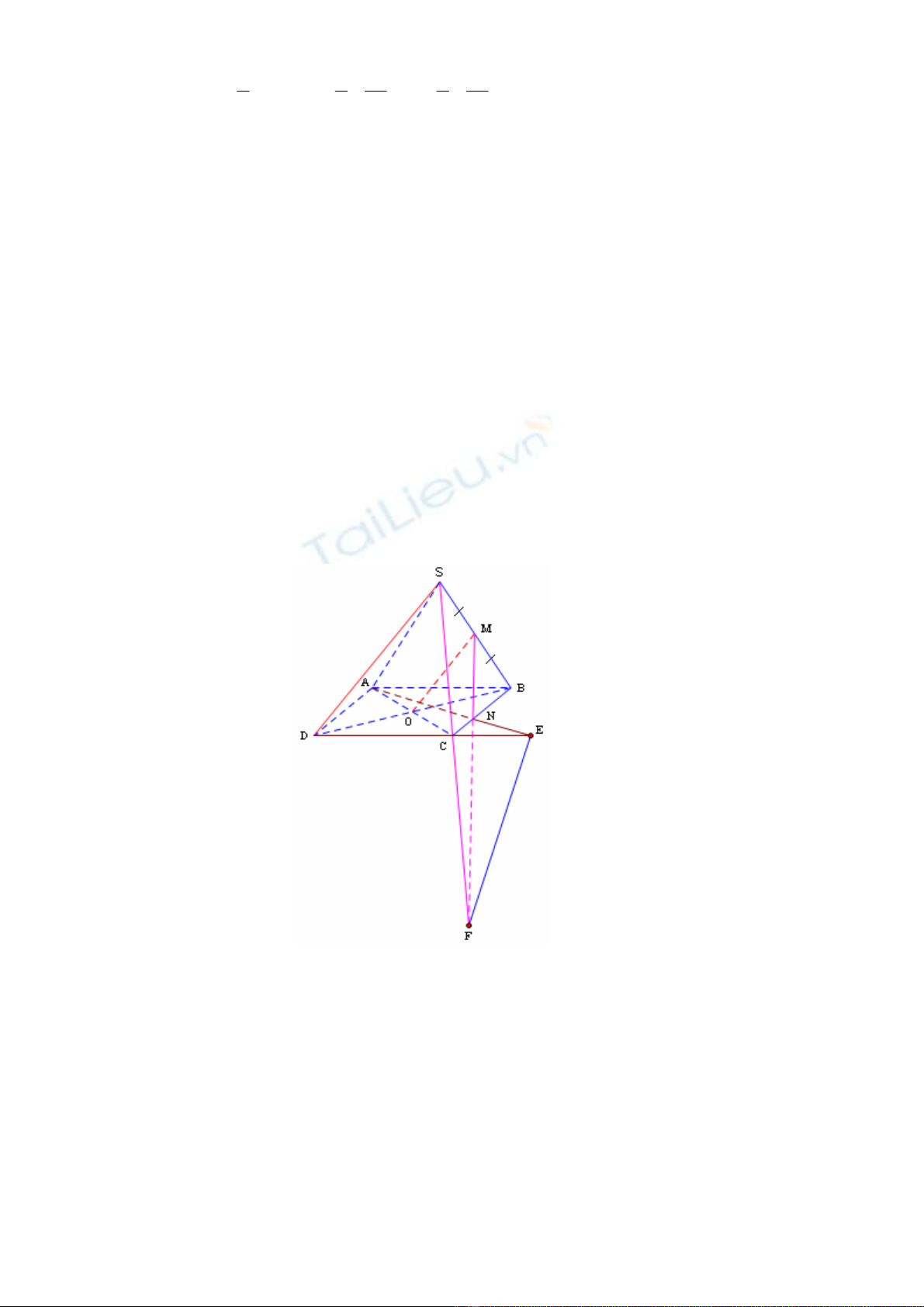
Câu 8 (1,5 điểm)
a) Chứng minh OM song song với mặt phẳng (SCD)
Trong tam giác SBD ta có OM là đường trung bình.
Do đó: OM // SD (0,25 ®iÓm)
Ta có: OM // SD OM // (SCD)
SD (SCD)
(0,25 ®iÓm)
b) Xác định giao tuyến của (SCD) và (AMN)
Trong (ABCD) ta có: AN CD E
E CD,CD (SCD) E (SCD)
E AN,AN (AMN) E (AMN)


E là điểm chung thứ 1 của (SCD) và (AMN) (1) (0,5 ®iÓm)
Trong (SBC) ta có: MN SC F
FSD,SC (SCD) E(SCD)
F MN, MN (AMN) E (AMN)


F là điểm chung thứ 2 của (SCD) và (AMN) (2) (0,25 ®iÓm)
Từ (1),(2) .Suy ra : giao tuyến của (SCD) và (AMN) là EF.
Hình (0,25 ®iÓm)
WWW.ToanCapBa.Net