Câu 1 (2,0 điểm).
a) Giải hệ phương trình:
3x + 2y = 8
2x - y = 3
b) Cho hai hàm số
( )
=2
:Pyx
và
( )
=−−+:2 3d y xm
với
m
là tham số. Tìm
m
để đường thẳng
( )
d
đi qua điểm
A
thuộc
( )
P
có hoành độ bằng
2.
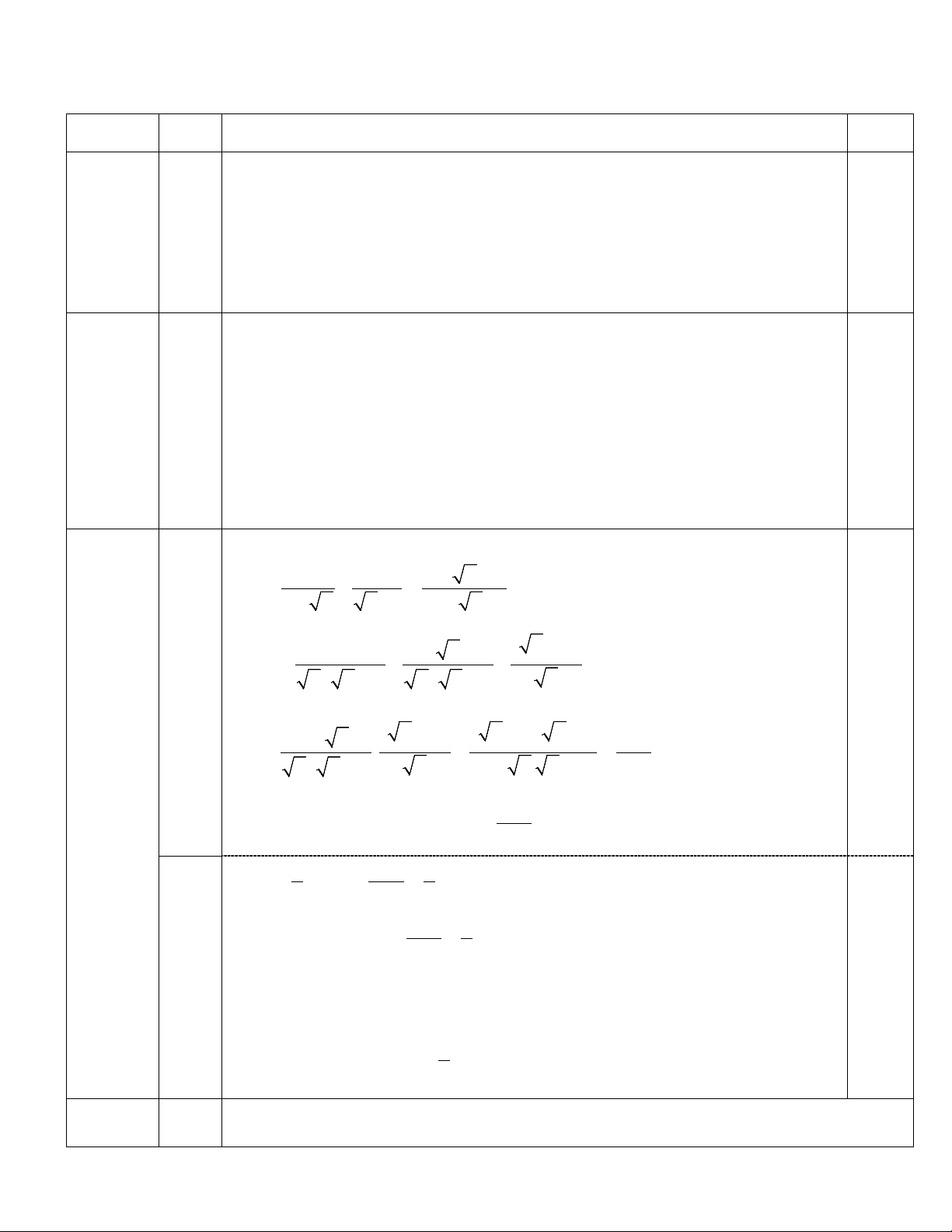
Câu 2 (2,0 điểm). Cho biểu thức: ) P =
11 x
:
x - x x 1 x - 2 x 1

+

−+

(với x > 0, x
1)
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để P >
1
2
.
Câu 3 (2,0 điểm). Cho phương trình
2( 2) 1 0x m xm+ + + −=
với
m
là tham số
a) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
b) Gọi
12
;xx
là hai nghiệm phân biệt của phương trình. Tìm m để
22
11 2 2
6x xx x−+ − =
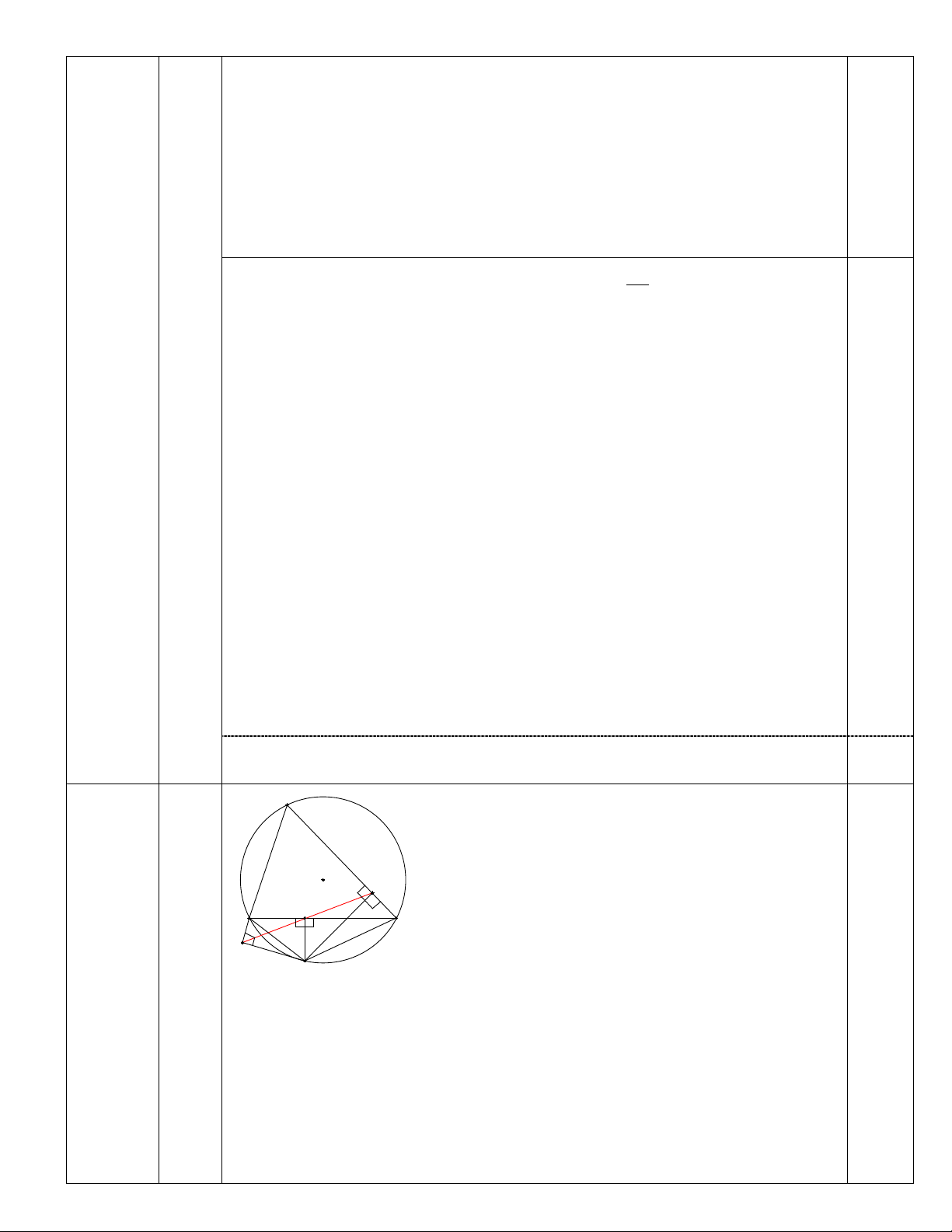
Câu 4: (3,0 điểm) Cho tam giác
ABC
( )
AB AC<
nội tiếp đường tròn tâm
O
.
M
là điểm nằm trên
cung
BC
không chứa điểm
A
. Gọi
D
,
E
,
F
lần lượt là hình chiếu của
M
trên
BC
,
CA
,
AB
.
a) Chứng minh bốn điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn
b) Chứng minh
D
,
E
,
F
thẳng hàng.
c) Chứng minh
BC AC AB
MD ME MF
= +
.
Câu 5( 1,0 điểm) : Cho
,,abc
là các số thực dương. Chứng minh rằng
( ) ( ) ( )
222
222
22 2
1.
3
555
abc
a bc b ca c ab
++≤
++ ++ ++
-------------------------------------Hết-----------------------------------
PHÒNG GD&ĐT HÀ TRUNG
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 LẦN 2
NĂM HỌC 2023- 2024
Môn thi: Toán
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề thi có 01 trang, gồm 05 câu
HƯỚNG DẪN CHẤM KHẢO SÁT LỚP 9
Câu
Ý
Nội dung
Điểm
Câu 1 a
a) Giải hệ phương trình:
3x + 2y = 8 3 2 8
2x - y = 3 4 2 6
7 14 2
23 1
xy
xy
xx
xy y
+=

⇔

−=

= =

⇔⇔

−= =

0,5
0,5
b
Vì điểm
A
nằm trên
( )
P
có hoành độ bằng
2.
Thay
2x=
vào
( )
2
: Pyx=
ta được
4y=
( )
2; 4 .A⇒
Vì
( )
Ad∈
. Thay
2; 4xy= =
vào đường thẳng
( )
d
ta được
4 2.2 3 44 30 50 5m mmm=− − +⇒++ −=⇒ +=⇒ =−
Vậy để đường thẳng
( )
d
đi qua điểm
A
nằm trên
( )
P
có hoành độ bằng
2
thì
5.m= −
0,5
0,5
Câu 2
a) ĐKXĐ: x > 0 ; x ≠ 1
11 x
P = :
x - x x 1 x - 2 x 1

+

−+

( ) ( )
( )
2
x1
1x
.x
x x1 x x1

−

= +

−−

( ) ( ) ( )( )
2
x1 x1 x1
1 x x - 1
.x
x x. x
x x1
− +−
+
= = =
−
Vậy: Với x > 0 ; x ≠ 1 thì
x - 1
x
P=
0,5
0,5
b) P >
1
2
<=>
x - 1 1
x2
>
Với x > 0, x
≠
1 thì
( )
x - 1 1
x2
2 x - 1 x
>
⇔>
x > 2⇔
(TM).
Vậy : Với x > 2 thì P >
1
2
.
0,5
0,5
Câu 3
(2,0đ)
a
(1,0đ
)
a)
2
( 2) 1 0x m xm+ + + −=
Ta có
22 2 2
4 ( 2) 4.1.( 1) 4 4 4 4 8b ac m m m m m m∆= − = + − − = + + − + = +
Ta có
22
0; 8 8 0;m mR m mR≥ ∀∈ ⇔ +≥> ∀∈
Vì
0∆>
nên phương trình luôn có hai nghiệm phân biệt với mọi m.
0,5
0,5
b) Với
0∆>
, theo hệ thức Vi-et, ta được
( )
12
12
2
1
b
xx m
a
xx m
−
+= =−+
= −
Theo bài ra
( )
22
1 12 2 12 1 2
22 6x xx x xx x x+ +− −+ =
( ) ( )
2
12 12 12
26xx xx xx⇔+ − −+ =
( ) ( ) ( )
2
2 2 1 26m mm⇔ + − −+ + =
2
4422 26mm m m⇔ + +− ++ +=
23 20mm⇔ + +=
12
1; 2mm⇒=− =−
Vậy,
{ }
1; 2m∈− −
thì phương trình có hai nghiệm thoả mãn
22
11 2 2
6x xx x−+ − =
0,25
0,25
0,25
0,25
4
(3,0đ)
a).Bốn điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn và bốn điểm
M
,
D
,
E
,
C
cùng thuộc một đường tròn.
Ta có:
MF AB⊥
nên
90MFB = °
.
0,25
l
1
2
2
1
O
F
B
C
A
M
D
E
MD BC⊥
nên
90MDB = °
.
Tứ giác
MDBF
có
90 90 180MFB MDB+ = °+ °= °
Do đó tứ giác
MDBF
nột tiếp.
Suy ra 4 điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn.
0,25
0,25
0,25
b).Chứng minh
D
,
E
,
F
thẳng hàng.
Vì tứ giác
MDBF
nội tiếp. Nên:
11
MD=
(cùng chắn
BF
).
Vì tứ giác
MDEC
nội tiếp nên
22
MD=
.
Mặt khác tứ giác
MBAC
nội tiếp.
Nên
1
BC=
(góc ngoài của tứ giác nội tiếp).
Do đó
12
MM=
(cùng phụ với
1;
BC
).
Suy ra:
12
DD=
.
Mà
2180D BDE+=°
Nên
1180D BDE+=°
.
Vậy,
D
,
E
,
F
thẳng hàng
0,25
0,25
0,25
0,25
c)
BC AC AB
MD ME MF
= +
Ta có :
AC AB AE EC AF FC AE EC AF FC
ME MF ME MF ME ME MF MF
+−
+= + =++−
21
tan tan tan tanAME M AMF M= ++ −
. Mà
12
MM=
Nên
tan tan
AC AB AME AMF
ME MF
+= +
.
0,25
0,25
Mặt khác: tứ giác
AFME
nội tiếp nên:
AME AFE BMD= =
AMF AEF DMC= =
Do đó:
tan tan
AC AB AME AMF
ME MF
+= +
tan tanBMD MDC= +
BD DC BD DC BC
MD MD MD MD
+
=+= =
.
0,25
0,25
Câu 5
(1điểm)
Ta có :
( ) ( ) ( )
222
222
22 2
555
abc
VT
a bc b ca c ab
=++
++ ++ ++
( )
( ) ( )
2 2 22
2 222 2
222 2
2
9 ( 2) 2
2
22
5
a aa a a
abc abc
abc abc
a bc
+
= ≤+
++ +
++ + +
++
Tương tự rồi cộng vế với vế của các BĐT ta được :
222
22 2
222
91
222
abc
VT a bc b ca c ab
≤+++
+++
D
ấu “=” xảy ra khi
.abc= =
Ta chứng minh:
222
22 2
1
222
abc
Aa bc b ca c ab
=++≤
+++
.
Ta có:
222
22 2
3111
-
2222
222
abc
Aa bc b ca c ab
=− +− +−
+++
22 2
1
2222
bc ca ab
a bc b ca c ab

= ++

+++

( )
( )
( )
( )
( )
( )
222
2 22
31 1
-
22 2
2. 2. 2.
1
bc ca ab
A
bc ab ac ca bc ab ab ca bc
A


= ++ ≥


+++

≤
Do đó:
9 12VT ≤+
hay
1.
3
VT ≤
Vậy:
( ) ( ) ( )
222
222
22 2
1.
3
555
abc
a bc b ca c ab
++≤
++ ++ ++
0,25
0,25
0,25
0,25
Lưu ý: