TRƯỜNG THCS MINH KHAI
ĐỀ CHÍNH THỨC
ĐỀ A
KHẢO SÁT NĂNG LỰC HỌC SINH LỚP 9
NĂM HỌC 2023 - 2024
Môn thi: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Ngày thi: 22/3/2024
(Đề thi có 05 câu, gồm 01 trang)
Câu I (2,0 điểm). Cho biểu thức:
32 6 3
23 1 3
− −+
= −−
−− + −
xx x x
Pxx x x
với
0; 9≥≠xx
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi
3 22= −
x
.
Câu II (2,0 điểm).
1. Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
( ): .= +d y ax b
Tìm
,ab
để đường thẳng
()d
có hệ số góc bằng
3
và đi qua điểm
( 1; 2)M−
.
2. Giải hệ phương trình:
xy2
3x 2y 11
−=
+=
Câu III (2,0 điểm).
1. Giải phương trình:
23 20xx− +=
.
2. Cho phương trình
22
2 20x mx m− − −=
(
m
là tham số). Tìm các giá trị của
m
để phương trình có hai nghiệm
12
,xx
(với
12
xx<
) thỏa mãn hệ thức
2
2 1 12
2 3 3 34x x xx m m− − = ++
.
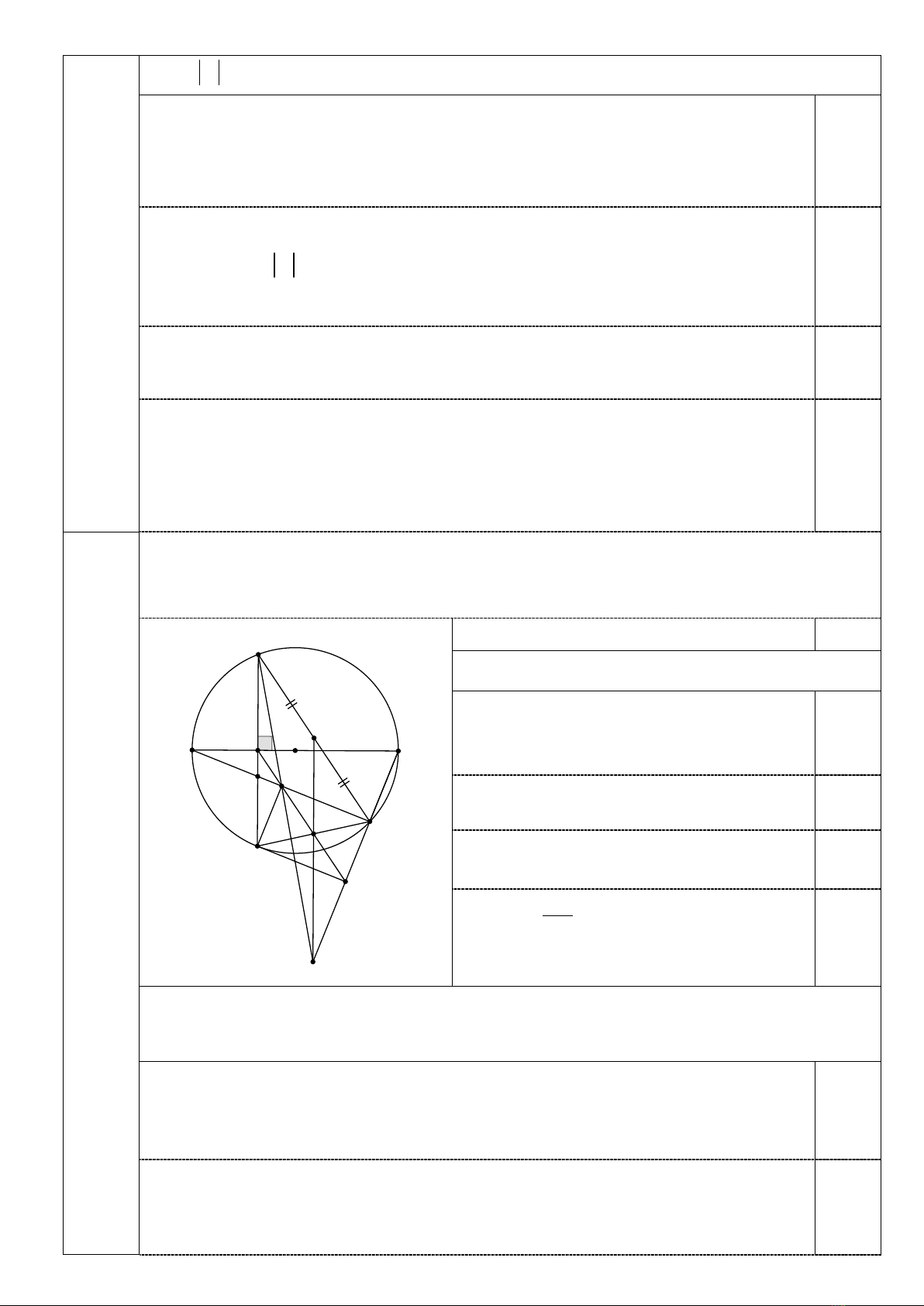
Câu IV (3,0 điểm). Cho đường tròn tâm (O) đường kính
AB
, lấy điểm
H
thuộc
đường kính
AB
, qua điểm
H
kẻ dây
CD
vuông góc với đường kính
AB
, lấy điểm
E
thuộc cung nhỏ
BD
(
E
khác
B
và
D
);
AE
cắt CD tại điểm
F
.
1. Chứng minh: Tứ giác
BEFH
nội tiếp.
2. Chứng minh:
24. .CD AH HB=
3. Đường thẳng đi qua
H
song song với
CE
, cắt đường thẳng
AE
và
BE
lần
lượt tại
I
và
K
. Gọi G là giao điểm của DE và IK, M là trung điểm của đoạn
thẳng CE. Chứng minh:
DI AE⊥
và ba đường thẳng CI, MG, BE đồng quy.
Câu V (1,0 điểm). Cho các số thực không âm
,,xyz
thỏa mãn
3.xy yz zx xyz++=
Tìm giá trị nhỏ nhất của biểu thức
222
3
111 2
xyz
Q xyz
yzx
=+++
+++
.
-------------------------------------- HẾT ----------------------------------------------
Họ và tên thí sinh: ..............................................................................
Chữ ký của CBCT1: ........................................................................
SBD: ................................................................
Chữ ký của CBCT2: ................................