SỞ GIÁO DỤC VÀ ĐÀO
TẠO
YÊN BÁI
ĐỀ CHÍNH THỨC
(Đề có 01 trang)
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2009-2010
MÔN TOÁN
Thời gian làm bài 120 phút không kể giao đề
Bài 1(2,0 điểm):
1- Cho hàm số xy
1
a) Tìm các giá trị của
y
khi: 0
x; 1
x
b) Vẽ đồ thị của hàm số trên mặt phẳng toạ độ.
2- Không dùng máy tính cầm tay:
a) Giải phương trình: 02
2 xx
b) Giải hệ phương trình:
123
32
yx
yx
Bài 2(2,0 điểm): Giải toán bằng cách lập phương trình:
Tìm hai số có tổng bằng 5 và tích bằng 6.
Bài 3(2,0 điểm): Cho: xy
xyyx
yx
yxyx
M2222 2
1- Tìm điều kiện để
M
có nghĩa.
2- Rút gọn
M
(với điều kiện
M
có nghĩa)
3- Cho 3 yyN . Tìm tất cả các cặp số );( yx để NM
Bài 4(3,0 điểm):
Độ dài các cạnh của một tam giác ABC vuông tại A, thoả mãn các hệ thức sau:
AB =
x
, AC = 1
x, BC = 2
x
1- Tính độ dài các cạnh và chiều cao AH của tam giác.
2- Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của
phần thuộc nửa hình tròn nhưng ở ngoài tam giác.
3- Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỷ số diện
tích giữa các phần do các dây cung AB và AC tạo ra.
Bài 5(1,0 điểm): Tính
P
= 22 yx và Q = 20092009 yx
Biết rằng: 0
x, 0
y , yxyxyx 1
---------- Hết ------------
Họ và tên thí sinh:..................................................................Phòng
thi:..............SBD:.......................
Họ và tên, chữ ký giám thị 1
...................................................................
Họ và tên, chữ ký giám thị 2
...................................................................
ĐÁP ÁN-HƯỚNG DẪN CHẤM THI VÀO LỚP 10 THPT
NĂM HỌC 2009-2010
MÔN TOÁN (ĐỀ CHÍNH THỨC)
Điể
m Nội dung
Bài 1(2,0 điểm):
1- Cho hàm số xy
1
a) Tìm các giá trị của
y
khi: 0
x; 1
x
b) Vẽ đồ thị của hàm số trên mặt phẳng toạ độ.
2- Không dùng máy tính cầm tay:
a) Giải phương trình: 02
2 xx
b) Giải hệ phương trình:
)2(123
)1(32
yx
yx
0,25
0,25
0,25
0,25
1-(1,0 đ)
a) (0,5 đ)
* Khi
x
= 0, ta có
y
= 1+ 0 = 1 hay
y
=
1
* Khi
x
= -1, ta có
y
= 1-1 = 0 hay
y
=
0
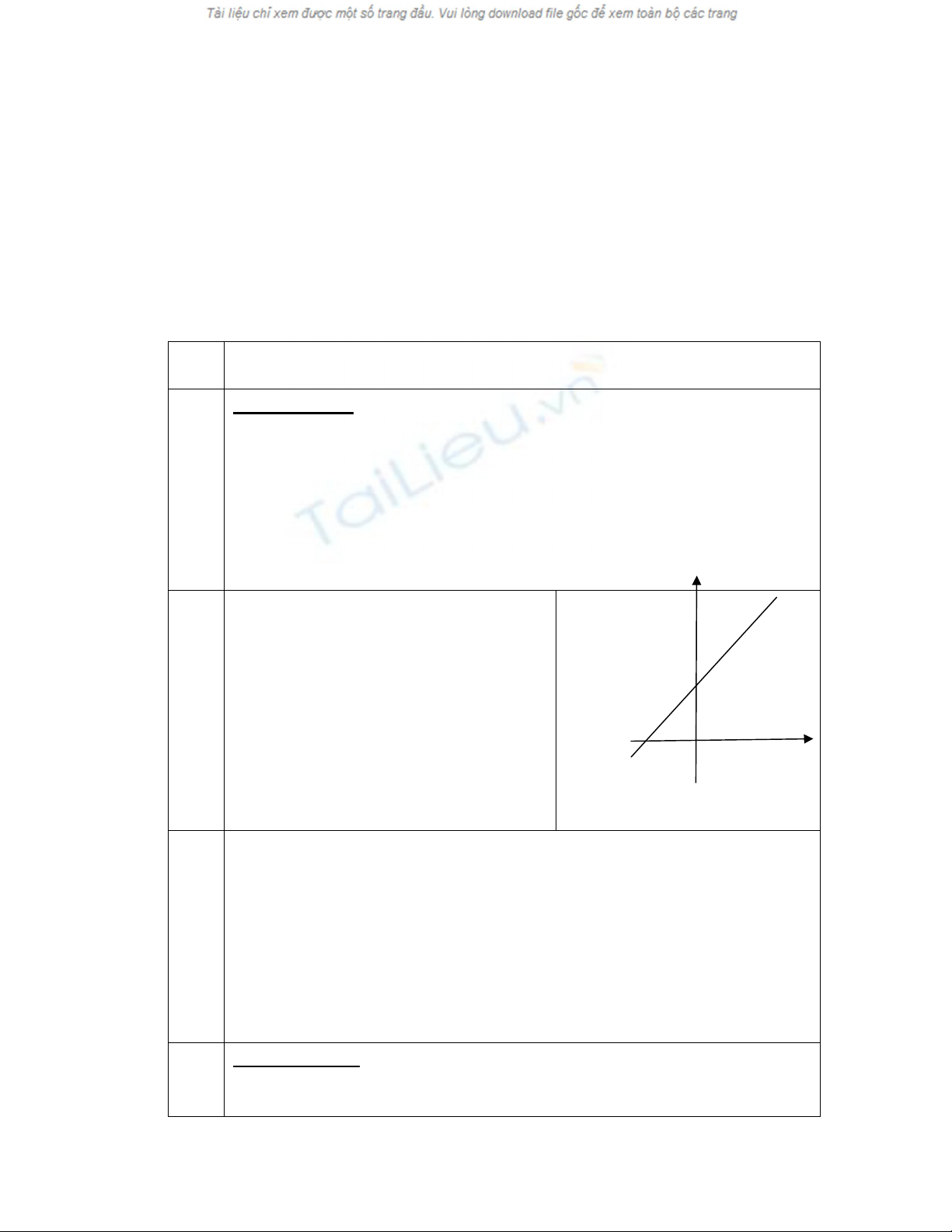
b) (0,5 đ)
* Xác định hai điểm (0; 1) và (-1; 0) trên
mặt phẳng toạ độ.
* Đồ thị hàm sốxy
1 (hình vẽ)
y
xy
1
1
-1 0
x
0,25
0,25
0,25
0,25
2-(1,0 đ)
a) (0,5 đ)
* Vì a + b + c = 1+1+(-2) = 1+ 1-2 = 0
* Phương trình đã cho có hai nghiệm:
x
1 = 1,
x
2 = -2
b) (0,5 đ)
* Lấy (1) + (2), ta có 4
x
= 4 <=>
x
= 1
* Thay
x
=1 vào 32
yx ta có 1 + 2
y
= 3 <=>
y
=1
Nghiệm của hệ phương trình đã cho là :
1
1
y
x
0,25
Bài 2(2,0 điểm): Giải toán bằng cách lập phương trình:
Tìm hai số có tổng bằng 5 và tích bằng 6.
* Gọi hai số phải tìm là
x
và
y
.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
* Vì tổng của hai số bằng 5, nên ta có
y
x
= 5
* Vì tích hai số bằng 6, nên ta có:
xy
= 6
* Ta có hệ phương trình:
6
5
xy
yx
* Các số
x
và
y
là nghiệm của phương trình: X2 -5X + 6 = 0 (1)
* Ta có
= 25-24 = 1> 0 =>
* (1) có hai nghiệm: 3
15
1
X, 2
15
2
X
* Hai số phải tìm là 2 và 3.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Bài 3(2,0 điểm): Cho xy
xyyx
yx
yxyx
M2222 2
1- Tìm điều kiện để
M
có nghĩa
2- Rút gọn
M
(với điều kiện
M
có nghĩa)
3- Cho 3 yyN . Tìm tất cả các cặp số );( yx để NM
1-(0,5 đ)
* Để
M
có nghĩa, ta có:
0
0
xy
yx
* <=> 0,0,
yxyx (1)
2-(0,75 đ)
* Với 0,0,
yxyx ta có: xy
yxxy
yx
yx
M)()( 2
*
M
=
y
x
y
x
* yM 2
3-(0,75 đ)
* Để 3yy có nghĩa thì 0
y (2)
Với 0,0,
yxyx (kết hợp (1) và (2)), ta có 32 yyy
* <=> 03)(2)( 23 yy đặt
= y,
> 0, ta có 032 23 aa
* <=>
3)(1()1)(1(2)1)(1()22()1(0 2223 aaaaaaaaaa
<=>
=1 > 0 (vì 33
2 aa =
3
)
3
(2a> 0). Do
=1 nên
y
= 1 > 0
Vậy các cặp số (
x
;
y
) phải tìm để NM
là:
x
tuỳ ý
0,
1;
y
= 1
Bài 4(3,0 điểm):
Độ dài các cạnh của một tam giác ABC vuông tại A, thoả mãn các hệ
thức sau: AB =
x
, AC = 1
x , BC = 2
x
1- Tính độ dài các cạnh và chiều cao AH của tam giác.
2- Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích
của phần thuộc nửa hình tròn nhưng ở ngoài tam giác.