
D báo b ng mô hình ARIMA ự ằ
(AutoRegressive Integrated Moving Average)
1. Tính d ng và tính mùa vừ ụ
a. Tính d ngừ
N u m i chu i th i gian g i là d ng thì trung bình, ph ng sai, đ ng ph ng sai (t iế ỗ ỗ ờ ọ ừ ươ ồ ươ ạ
các đ tr khác nhau) s gi nguyên không đ i dù cho chúng đ c xác đ nh vào th iộ ễ ẽ ữ ổ ượ ị ờ
đi m nào đi n a.ể ữ
Trung bình: E(Yt)=const
Ph ng sai: Var(Yươ t)=const
Đ ng ph ng sai: Covar(Yồ ươ t,Yt-k)=gk
Đ xem m t chu i th i gian có d ng hay không, ta có th s d ng Đ th c a Yt theoể ộ ỗ ờ ừ ể ử ụ ồ ị ủ
th i gian, Đ th t t ng quan m u (Sample Auto Correlation), hay ki m đ nh b cờ ồ ị ự ươ ẫ ể ị ướ
ng u nhiên (ki m đ nh Dickey-Fuller)ẫ ể ị
N u chu i Yt không d ng, ta có th l y sai phân b c 1. Khi đó chu i sai phân b c 1ế ỗ ừ ể ấ ậ ỗ ậ
(Wt) s có th d ng. Sai phân b c 1: Wẽ ể ừ ậ t=Yt-Yt-1
N u chu i sai phân b c 1 (Wt) không d ng, ta có th l y sai phân b c 2. Khi đó chu iế ỗ ậ ừ ể ấ ậ ỗ
sai phân b c 2 có th d ng. Sai phân b c 2: Vậ ể ừ ậ t=Wt-Wt-1
b. Tính mùa vụ
N u sai phân b c 2 mà ch a d ng, có th chu i Yế ậ ư ừ ể ỗ t có y u t mùa v . (N u có y u tế ố ụ ế ế ố
mùa v , t c là chu i v n ch a d ng). ụ ứ ỗ ẫ ư ừ
N u c sau m th i đo n, SAC l i có giá tr cao. Khi đó Yế ứ ờ ạ ạ ị t có tính mùa v v i chu kỳ mụ ớ
th i đo n. Ph ng pháp đ n gi n nh t đ kh tính mùa v là l y sai phân th mờ ạ ươ ơ ả ấ ể ử ụ ấ ứ
Zt=Yt-Yt-m
2. Nh n d ng mô hìnhậ ạ
Mô hình ARIMA (hay còn g i là ph ng pháp Box-Jenkin)ọ ươ
Nh n d ng mô hình t c là xác đ nh p, d, q trong ARIMA(p,d,q)ậ ạ ứ ị
p: d a vào SPACự
q: d a vào SACự
d: d a vào s l n l y sai phân đ làm cho chu i d ngự ố ầ ấ ể ỗ ừ
3. Ki m tra chu n đoán mô hìnhể ầ
Mô hình ARIMA t t có RMSE nh và sai s là nhi u tr ng: Sai s có phân ph i chu n,ố ỏ ố ễ ắ ố ố ẩ
và đ th SAC gi m nhanh v 0ồ ị ả ề
Tìm ki m mô hình ARIMA phù h p là m t quá trình th và sai.ế ợ ộ ử
1
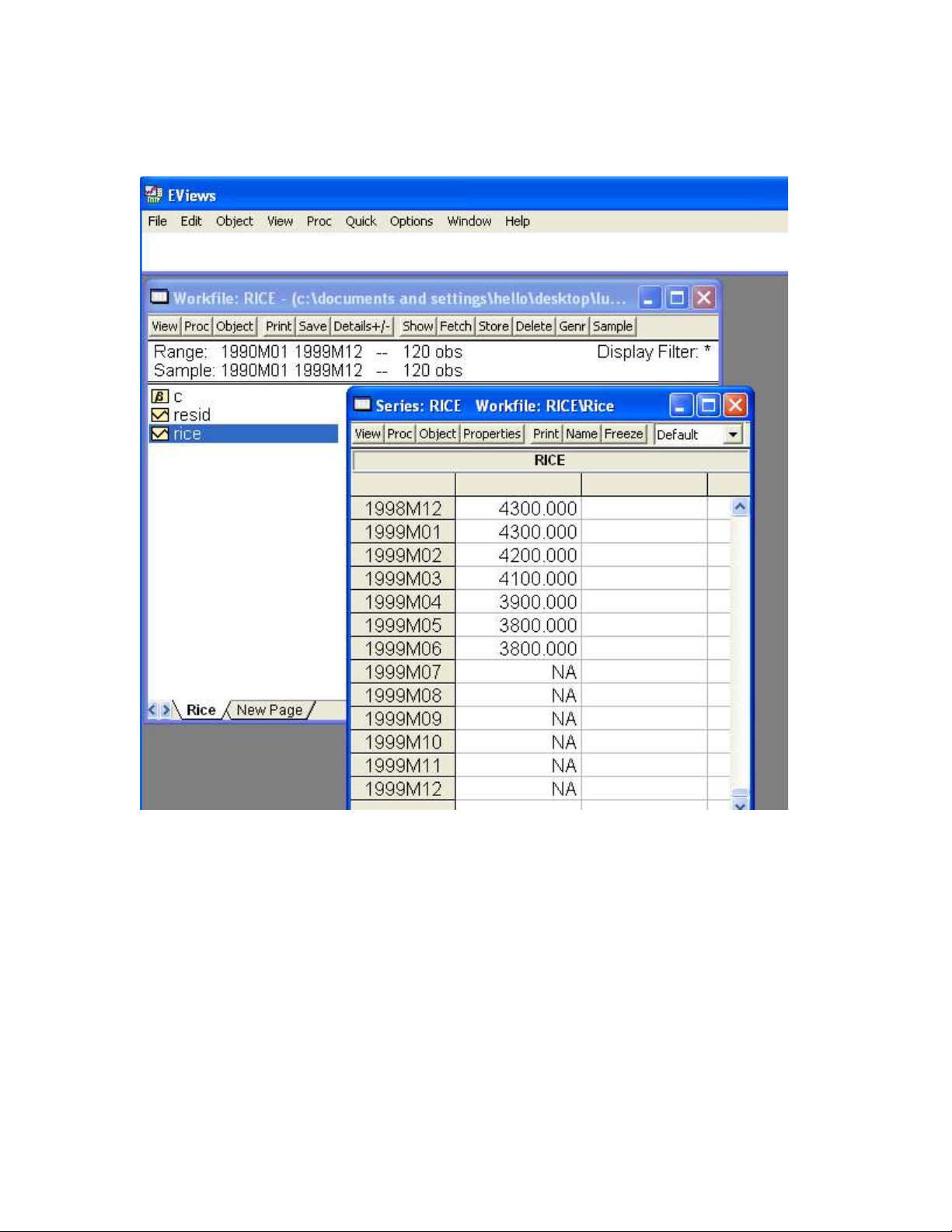
Ví d d báo giá g oụ ự ạ
1. D li uữ ệ
Hình 1
2. Xem chu i Rice có d ng không?ỗ ừ
2
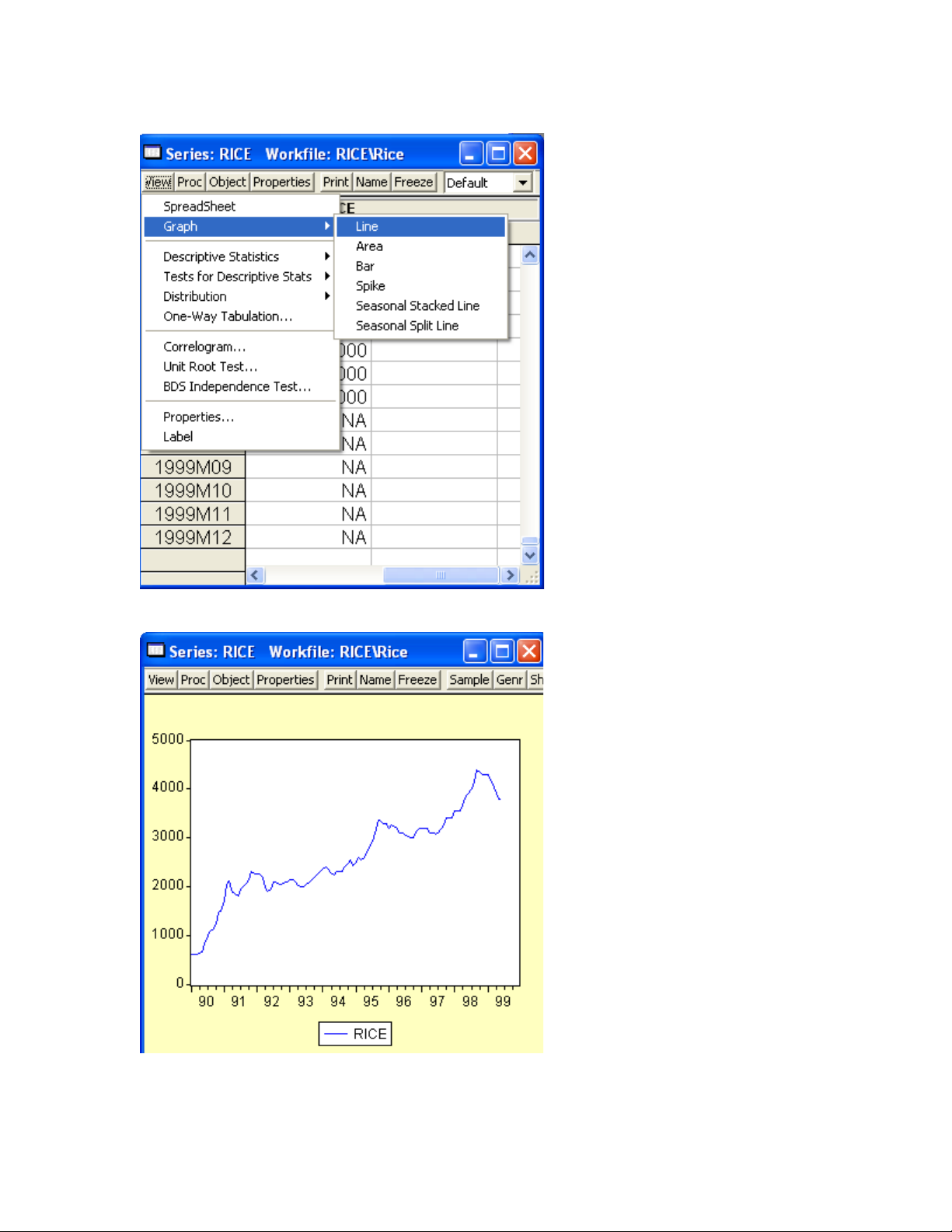
Hình 2
Hình 3
3
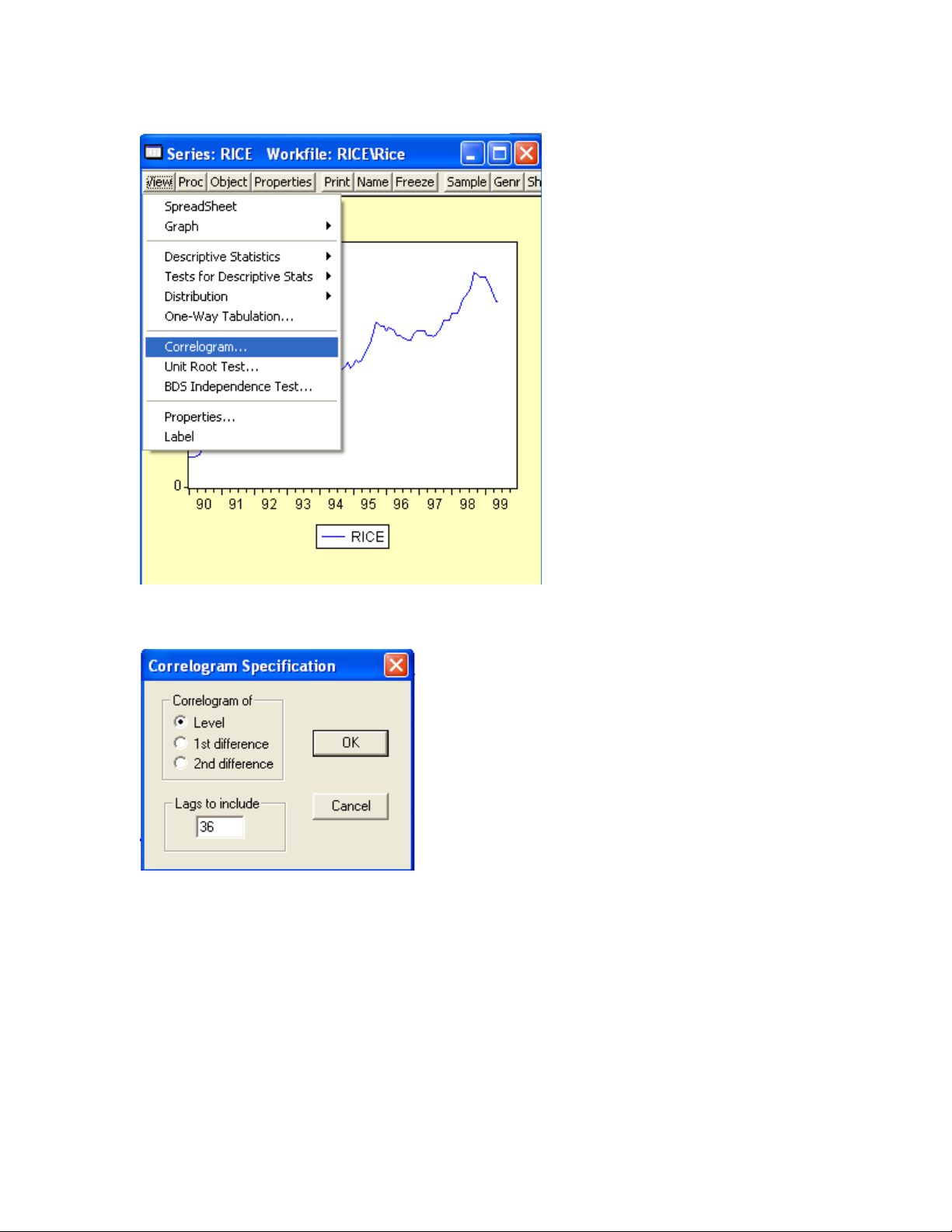
Hình 4
Hình 5
4
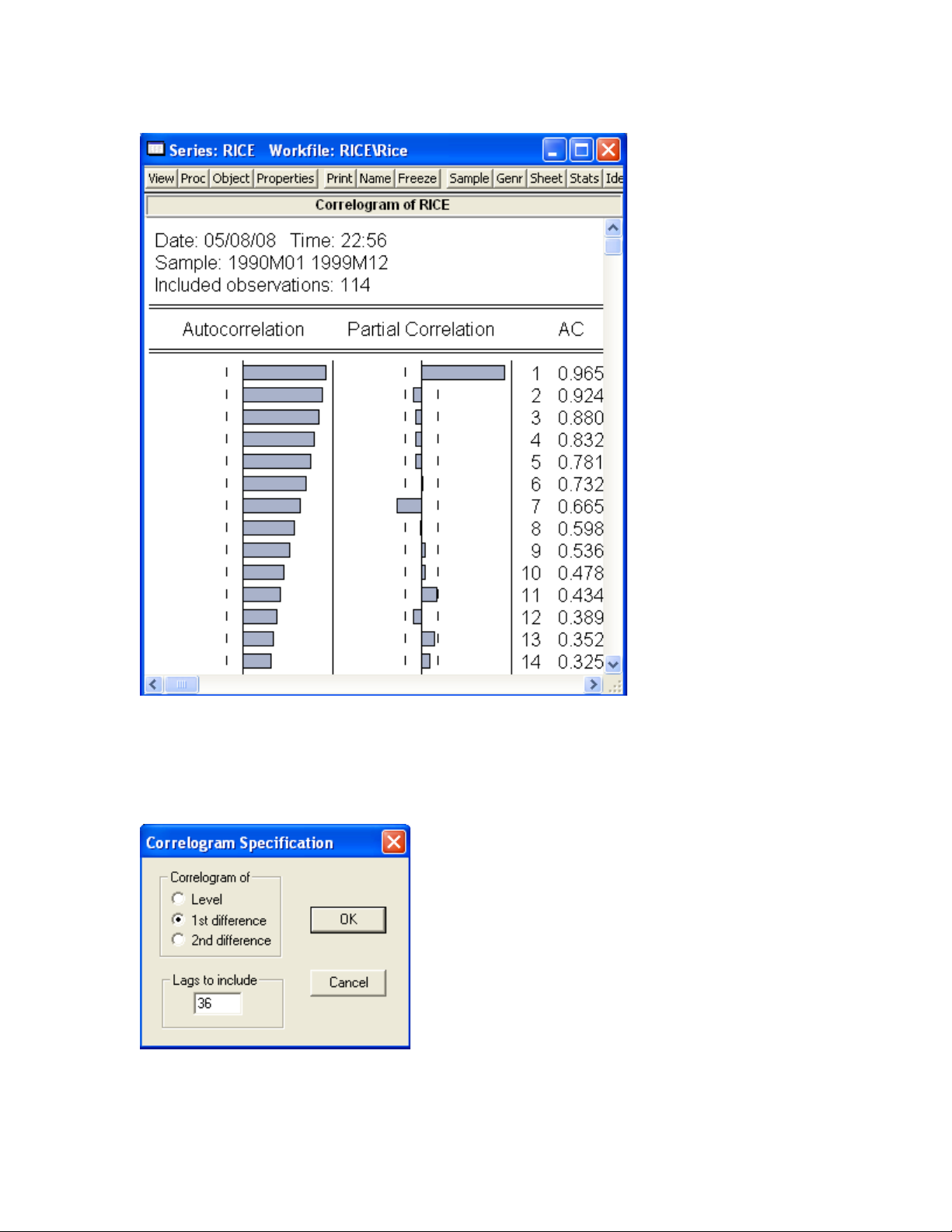
Hình 6
Nh v y chu i RICEư ậ ỗ t ch a d ng. Ta có th l y sai phân b c 1 c a chu i này.ư ừ ể ấ ậ ủ ỗ
Th xem đ th Correlogram c a chu i sai phân b c 1ử ồ ị ủ ỗ ậ
Hình 7
5


























