
M t s gi i pháp v gi i ph ng trình vô t dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình ộ ố ả ề ả ươ ỉ ọ ỏ ớ ườ
Chinh
PH N I. ẦM ĐUỞ Ầ
I. Đt v n đặ ấ ề
1. Lí do lí lu nậ
Albert Einstein đã nói: “Toán h c thu n túy, theo cách riêng c a nó, là thi caọ ầ ủ
c a t duy logic”. Do v y, có r t nhi u nh ng th c m c xoay quanh vi c h c nhi uủ ư ậ ấ ề ữ ắ ắ ệ ọ ề
toán li u có phi th c t trong khi đi s ng không c n suy nghĩ quá nhi u đn nh ngệ ự ế ờ ố ầ ề ế ữ
con s ? Tuy nhiên, th c t ch ng minh r ng, m i ki n th c liên quan đn toán h c,ố ự ế ứ ằ ọ ế ứ ế ọ
đu có tác d ng chung là làm cho b não c a con ng i t duy logic h n, khoa h cề ụ ộ ủ ườ ư ơ ọ
h n và sáng t o h n, nó giúp cho ng i h c có kh năng suy nghĩ tr u t ng vàơ ạ ơ ườ ọ ả ừ ượ
trong m t ch ng m c nh t đnh nào đó nó làm cho chúng ta m nh m h n trong m iộ ừ ự ấ ị ạ ẽ ơ ọ
quy t đnh. ế ị
Chính vì đi u này, b n thân tôi là m t giáo viên v n luôn tâm đc trong vi cề ả ộ ố ắ ệ
đnh h ng các em h c t t môn Toán, luôn tìm tòi đi m i đ giúp các em ngàyị ướ ọ ố ổ ớ ể
càng hoàn thi n h n các ki n th c toán h c. M c dù ch ng trình sách giáo khoaệ ơ ế ứ ọ ặ ươ
hi n hành đã đc ch n l c nh ng ki n th c r t c b n, phù h p cho m i điệ ượ ọ ọ ữ ế ứ ấ ơ ả ợ ọ ố
t ng. Tuy nhiên, không ph i b t c d ng toán nào các em cũng có th n m b tượ ả ấ ứ ạ ể ắ ắ
đc, trong s đó có d ng toán ph ng trình vô t , m t d ng toán ph bi n trongượ ố ạ ươ ỉ ộ ạ ổ ế
các đ thi h c sinh gi i văn hóa các c p, đ thi vào l p 10 và thi gi i toán trên máyề ọ ỏ ấ ề ớ ả
tính c m tay Casio. ầ
2. Lí do th c ti nự ễ
Đ làm t t vi cể ố ệ b i d ng h c sinh h c Toánồ ưỡ ọ ọ , tôi nh n th y ậ ấ ch cung c p choỉ ấ
các em m t s ki n th c c b n thông qua ộ ố ế ứ ơ ả vi c ệlàm bài t p ho c làm nhi u bài t pậ ặ ề ậ
khó mà giáo viên phân lo i c p đ t d đn khó là ch a đ, mà chúng ta ạ ấ ộ ừ ễ ế ư ủ ph i bi tả ế
phân chia theo t ng ki u lo i bài t p và đnh h ng ph ng pháp gi i cho t ngừ ể ạ ậ ị ướ ươ ả ừ
d ng, đng th i rèn luy n cho h c sinh có thói quen suy nghĩ tìm tòi l i gi i c aạ ồ ờ ệ ọ ờ ả ủ
m t bài toán trên c s các ki n th c đã h c.ộ ơ ở ế ứ ọ
Qua nhi u năm th c t gi ng d y và b i d ng h c sinh gi i kh i 9, tôi nh nề ự ế ả ạ ồ ưỡ ọ ỏ ố ậ
th y h c sinh còn lúng túng r t nhi u khi g pấ ọ ấ ề ặ d ng ph ng trình vô t và th ng ạ ươ ỉ ườ có
nh ng sai sót khi gi i d ng bài t p này, h c sinh còn v ng m c v ph ng phápữ ả ạ ậ ọ ướ ắ ề ươ
gi i, quá trình gi i thi u logic và ch a ch t ch , ch a đ đi u ki n, ch a xét h tả ả ế ư ặ ẽ ư ủ ề ệ ư ế
các tr ng h p x y ra. Lí do là h c sinh ch a n m v ng các ki n th c v ph ngườ ợ ả ọ ư ắ ữ ế ứ ề ươ
trình có ch a bi n d i d u căn hay g i là ph ng trình vô tứ ế ướ ấ ọ ươ ỉ. Nên khi g p bài toánặ
gi i ph ng trình vô t , đa s h c sinh ch a phân bi t và ch a n m đc cácả ươ ỉ ố ọ ư ệ ư ắ ượ
ph ng pháp gi i đi v i t ng d ng bài t p, có nhi u bài toán đòi h i h c sinh ph iươ ả ố ớ ừ ạ ậ ề ỏ ọ ả
bi t v n d ng k t h p nhi u ki n th c và kĩ năng phân tích bi n đi đ đaế ậ ụ ế ợ ề ế ứ ế ổ ể ư
ph ng trình t d ng ph c t p v d ng đn gi n.ươ ừ ạ ứ ạ ề ạ ơ ả
Do đó ng i giáo viên c n ph i bi t s p x p các d ng toán t d đn khó,ườ ầ ả ế ắ ế ạ ừ ễ ế
phân lo i đc các d ng bài t p và đnh h ng ph ng pháp gi i cho t ng d ng đạ ượ ạ ậ ị ướ ươ ả ừ ạ ể
các em có th v n d ng linh ho t trong t ng tình hu ng c th , giúp h c sinh hi uể ậ ụ ạ ừ ố ụ ể ọ ể
sâu s c ắb n ch tả ấ c aủ t ng d ng toán và gi i đc các d ng bài toán m t cách thànhừ ạ ả ượ ạ ộ
th o. T đó rèn luy n cho h c sinh kĩ năng gi i toán và t duy sáng t o.ạ ừ ệ ọ ả ư ạ
Trang 1

M t s gi i pháp v gi i ph ng trình vô t dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình ộ ố ả ề ả ươ ỉ ọ ỏ ớ ườ
Chinh
V i nh ng lý do trên, tôi ch n đ tài: “ớ ữ ọ ề M t s gi i pháp v gi i ph ng trìnhộ ố ả ề ả ươ
vô tỉ dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình Chinh”ọ ỏ ớ ườ v i mong mu nớ ố
đc chia s m t vài kinh nghi m c a mình trong công tác gi ng d y cũng nh b iượ ẻ ộ ệ ủ ả ạ ư ồ
d ng h c sinh gi i đ các đng nghi p tham kh o, r t mong nh n đc s góp ýưỡ ọ ỏ ể ồ ệ ả ấ ậ ượ ự
chân thành c a các đng chí đ đ tài đc phát huy hi u quủ ồ ể ề ượ ệ ả, hoàn thi n h nệ ơ .
II. M c đích nghiên c uụ ứ
Đ tài: “ềM t s gi i pháp v gi i ph ng trình vô tộ ố ả ề ả ươ ỉ dành cho h c sinh gi iọ ỏ
l p 9 tr ng THCS Lê Đình Chinh”ớ ườ giúp h c sinh hi u sâu s c h n ọ ể ắ ơ b n ch tả ấ c aủ
t ng d ng bài toán ừ ạ và n m v ng ph ng pháp gi i c a t ng d ng, giúp cho h cắ ữ ươ ả ủ ừ ạ ọ
sinh bi t phân lo i và v n d ng ph ng pháp gi i m t cách linh ho t và có hi uế ạ ậ ụ ươ ả ộ ạ ệ
qu . Qua đó giúp h c sinh phát huy đc tính tích c c và tinh th n sáng t o trongả ọ ượ ự ầ ạ
h c t p, phát tri n năng l c t duy toán h c cho h c sinh, t o đng l c thúc đyọ ậ ể ự ư ọ ọ ạ ộ ự ẩ
giúp các em h c sinh có đc s t tin trong h c t p, hình thành ph m ch t sángọ ượ ự ự ọ ậ ẩ ấ
t o khi gi i toán và ni m đam mêạ ả ề , yêu thích b môn.ộ Thông qua đ tài này nh mề ằ
cung c p nh ng ki n th c c n thi t v ph ng pháp gi i toán, nh ng kinh nghi mấ ữ ế ứ ầ ế ề ươ ả ữ ệ
c th trong quá trình tìm tòi l i gi i giúp h c sinh rèn luy n các thao tác t duy lô-ụ ể ờ ả ọ ệ ư
gic, ph ng pháp suy lu n và kh năng sáng t o cho h c sinh. Trong đ tài l i gi iươ ậ ả ạ ọ ề ờ ả
đc ch n l c v i cách gi i h p lí, ch t ch , d hi u đm b o tính chính xác, tínhượ ọ ọ ớ ả ợ ặ ẽ ễ ể ả ả
s ph m. H c sinh t đc có th gi i đc nhi u d ng Toán, giúp h c sinh cóư ạ ọ ự ọ ể ả ượ ề ạ ọ
nh ng ki n th c toán h c phong phú đ h c t t môn Toán và qua đó hữ ế ứ ọ ể ọ ố ỗ tr h c sinhợ ọ
h c t t các môn h c khác.ọ ố ọ
PH N II.Ầ GI I QUY T V N ĐẢ Ế Ấ Ề
I. C s lí lu n c a v n đơ ở ậ ủ ấ ề
D ng toán ph ng trình vô tạ ươ ỉ là d ng toán r t quan tr ng trong ch ng điạ ấ ọ ươ ạ
s 9, đây là nh ng bài toán khó, th ng xu t hi n trong các đ thi h c sinh gi i, thiố ữ ườ ấ ệ ề ọ ỏ
vào l p 10... Các bài toán này r t phong phú v th lo i và v cách gi i, đòi h i h cớ ấ ề ể ạ ề ả ỏ ọ
sinh ph i v n d ng nhi u ki n th c, linh ho t trong bi n đi, s c s o trong l pả ậ ụ ề ế ứ ạ ế ổ ắ ả ậ
lu n và phát huy t i đa kh năng phán đoán. V i m c đích nh m nâng cao ch tậ ố ả ớ ụ ằ ấ
l ng d y và h c Toán, tôi thi t nghĩ c n ph i trang b cho h c sinh ph ng phápượ ạ ọ ế ầ ả ị ọ ươ
gi i cho t ng ki u lo i bài t p. Đ th c hi n t t đi u này, đòi h i giáo viên c nả ừ ể ạ ậ ể ự ệ ố ề ỏ ầ
xây d ng cho h c sinh nh ng kĩ năng nh quan sát, phân tích, nh n d ng bài toán,ự ọ ữ ư ậ ạ
l a ch n ph ng pháp gi i phù h p. T đó, hình thành cho h c sinh t duy tích c c,ự ọ ươ ả ợ ừ ọ ư ự
đc l p, kích thích tò mò ham tìm hi u và đem l i ni m vui cho các em, đng th iộ ậ ể ạ ề ồ ờ
kh i d y cho các em s t tin trong h c t p và ni m đam mê b môn. ơ ậ ự ự ọ ậ ề ộ
II. Th c tr ng v n đự ạ ấ ề:
Trong nh ng năm qua, tôi đã tr c ti p tham gia gi ng d y cữ ự ế ả ạ ũng nh b iư ồ
d ng đi tuy n h c sinh gi i 9 c a tr ng THCS Lê Đình Chinh và đã tr iưỡ ộ ể ọ ỏ ủ ườ ả
nghi m r t nhi u chuyên đ b i d ng h c sinh gi i, trong đó có chuyên đ “M tệ ấ ề ề ồ ưỡ ọ ỏ ề ộ
s gi i pháp gi i ph ng trình vô t ” và tôi cũng đt đc các thành tích trong côngố ả ả ươ ỉ ạ ượ
tác gi ng d y cả ạ ũng nh b i d ng h c sinh gi i. ư ồ ưỡ ọ ỏ
Tuy nhiên, khi áp d ng chuyên đ trên còn n ng v ph ng pháp li t kê cácụ ề ặ ề ươ ệ
bài toán, ch a phát huy đc hi u qu h c t p và k t qu đc th ng kê l i như ượ ệ ả ọ ậ ế ả ượ ố ạ ư
sau:
Trang 2
M t s gi i pháp v gi i ph ng trình vô t dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình ộ ố ả ề ả ươ ỉ ọ ỏ ớ ườ
Chinh
Năm
h cọL pớT ngổ
sốS l ng h cố ượ ọ
sinh làm đcượ S l ng h c sinhố ượ ọ
làm ch a ch t chư ặ ẽ S l ng h cố ượ ọ
sinh không làm
đcượ
SL T lỷ ệ SL T lỷ ệ SL T lỷ ệ
2015
- 2016
9A1 30 5 16% 11 37% 14 47%
9A2 31 4 12% 13 42% 15 46%
Qua b ng th ng kê trên tôi suy nghĩ tìm cách đ ả ố ể h c sinh n m v ng và gi iọ ắ ữ ả
thành th o các bài toán ạv ph ng trình vô tề ươ ỉ thì giáo viên nên phân lo i ạtheo d ngạ
bài t pậ t d đn khóừ ễ ế , m i lo i bài t p phân theo t ng d ng khác nhau, qua m iỗ ạ ậ ừ ạ ỗ
d ng ạc n ầcó ví d minh ch ng và xây d ng ph ng pháp gi i chung cho t ng d ng.ụ ứ ự ươ ả ừ ạ
V i nh ng ý t ng đó tôi đã th hi n trong đ tài nghiên c u “ớ ữ ưở ể ệ ề ứ M t s gi i pháp vộ ố ả ề
gi i ph ng trình vô tả ươ ỉ giành cho h c sinh gi i l p 9 tr ng THCS Lê Đình Chinh”ọ ỏ ớ ườ .
Sau khi đa ra t p th t chuyên môn th o lu n và áp d ng vào th c ti n tôi nh nư ậ ể ổ ả ậ ụ ự ễ ậ
th y h c sinh h ng thú, ch đng h n trong h c t p và khi g p d ng toán ph ngấ ọ ứ ủ ộ ơ ọ ậ ặ ạ ươ
trình vô t thì h c sinh không chán n n mà ỉ ọ ả đam mê phân tích nh n d ng tìậ ạ m cách
gi i bài toánả, từ đó ngày càng rèn luy n đc cho h c sinh kĩ năng gi i toán có khoaệ ượ ọ ả
h c, l p lu n logic và ch t ch . ọ ậ ậ ặ ẽ
III. Các gi i pháp đã ti n hành đ gi i quy t v n đả ế ể ả ế ấ ề
Gi i pháp 1: Phân tích cho h c sinh hi u v các ki n th c c b n c n n mả ọ ể ề ế ứ ơ ả ầ ắ
v ng.ữ
Gi i pháp 2: H ng d n cho h c sinh hi u các d ng bài t p s d ng cáchả ướ ẫ ọ ể ạ ậ ử ụ
gi i ph ng trình vô t b ng ph ng pháp nâng lên lũy th aả ươ ỉ ằ ươ ừ
Gi i pháp 3: H ng d n cho h c sinh hi u các d ng bài t p gi i ph ngả ướ ẫ ọ ể ạ ậ ả ươ
trình vô t b ng ph ng pháp đt n phỉ ằ ươ ặ ẩ ụ
V n d ng các gi i pháp trên, tôi ti n hành c th các b c nh sau:ậ ụ ả ế ụ ể ướ ư
1. Gi i pháp 1ả. Phân tích cho h c sinh hi u v các ki n th c c b n c nọ ể ề ế ứ ơ ả ầ
n m v ng.ắ ữ
Các ki n th c c b n t ng h p thành b ng sau, yêu c u h c sinh c n n mế ứ ơ ả ổ ợ ả ầ ọ ầ ắ
v ng, c th :ữ ụ ể
A
(A
0)
2
A A=
AB A B(A 0;B 0)=
A A (A ; B 0)
BB
= >
2
A B A B (B 0)= =
A A B (B 0)
B
B= >
( )
2
2
C A B
C(A 0;A B )
A B
A B =
−
m
( )
C A B
C(A 0;B 0; A B)
A B
A B
=
−
m
Trang 3

M t s gi i pháp v gi i ph ng trình vô t dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình ộ ố ả ề ả ươ ỉ ọ ỏ ớ ườ
Chinh
2
A B A B(A 0;B 0)=
2
A B A B(A 0; B 0)= − <
A AB (AB 0; B 0)
B B
=
3
A( A R)∀
( )
3
3
A A=
3 3 3
AB A. B=
3
3
3
A A (B 0)
BB
=
Các ki n th c v giá tr tuy t đi, h ng đng th c, phân tích đa th c thànhế ứ ề ị ệ ố ằ ẳ ứ ứ
nhân t , chia đa th c cho đa th c, gi i ph ng trình, b t tr ng b c nh t m t n,ử ứ ứ ả ươ ấ ươ ậ ấ ộ ẩ
b t đng th c Cauchy...ấ ẳ ứ
Bên canh nh ng yêu câu trên, hoc sinh c n nhân biêt đc nh ng dang c ban + ư + ầ + ươ+ ư + ơ ,
cua ph ng trinh vô t , đông th i n m v ng ph ng phap giai cu thê cho t ng dang , ươ ỉ ơ ắ ữ ươ , + , ư +
bai t p, c th nh sau:ậ ụ ể ư
2. Gi i pháp 2. Gi i ph ng trình vô t b ng ph ng pháp nâng lên lũyả ả ươ ỉ ằ ươ
th aừ
2.1. D ng 1ạ: Ph ng trình vô t có d ngươ ỉ ạ :
f (x) m=
(1)
Trong đó f(x) là bi u th c ch a x và mể ứ ứ
R .
a) Phân tích: d ng này yêu c u h c sinh c n n m rõ v trái là m t bi uỞ ạ ầ ọ ầ ắ ế ộ ể
th c không âm. ứN u m < 0 thì đng th c không x y ra nên ph ng trình vô nghi m.ế ẳ ứ ả ươ ệ
N u mế
0 thì ph ng trình t n t i v y khi mươ ồ ạ ậ
0 thì ph ng trình không c n tìmươ ầ
đi u ki n khi đó ta tìm cách b d u căn b c hai r i gi i ph ng trình v a tìm đc.ề ệ ỏ ấ ậ ồ ả ươ ừ ượ
V y ph ng trình (1) mà m < 0 k t lu n ph ng trình vô nghi m ta không gi i, mậ ươ ế ậ ươ ệ ả
0 bình ph ng hai v r i gi i ph ng trình v a tìm đc.ươ ế ồ ả ươ ừ ượ
b) Ph ng phap giai ươ
(1)
2
f (x) m =
Ti p t c gi i ph ng trình f(x) = mế ụ ả ươ 2 suy ra x r i k t lu n nghi m c aồ ế ậ ệ ủ
ph ng trình. ươ
c) Các ví d minh h aụ ọ
Ví d 1. ụGi i ph ng trình: ả ươ
x 5 3− =
Phân tích: Ph ng trình đã cho có t n t i không? Vì sao? (Ph ng trình đãươ ồ ạ ươ
cho có t n t i vì v trái ồ ạ ế
x 5 0−
và v ph i 3 > 0). V y đi v i d ng này khôngế ả ậ ố ớ ạ
c n tìm đi u ki n.ầ ề ệ
Đ gi i ph ng trình đã cho ta làm nh th nào? (Làm m t d u căn b c haiể ả ươ ư ế ấ ấ ậ
b ng cách bình ph ng hai v r i gi i ph ng trình v a tìm đc)ằ ươ ế ồ ả ươ ừ ượ
Gi iả
Ta có:
x 5 3− =
( )
22
x 5 3 − =
x 5 9
− =
x 9 5
= +
x 14
=
V y nghi m c a ph ng trình đã cho là x = 14ậ ệ ủ ươ
Trang 4
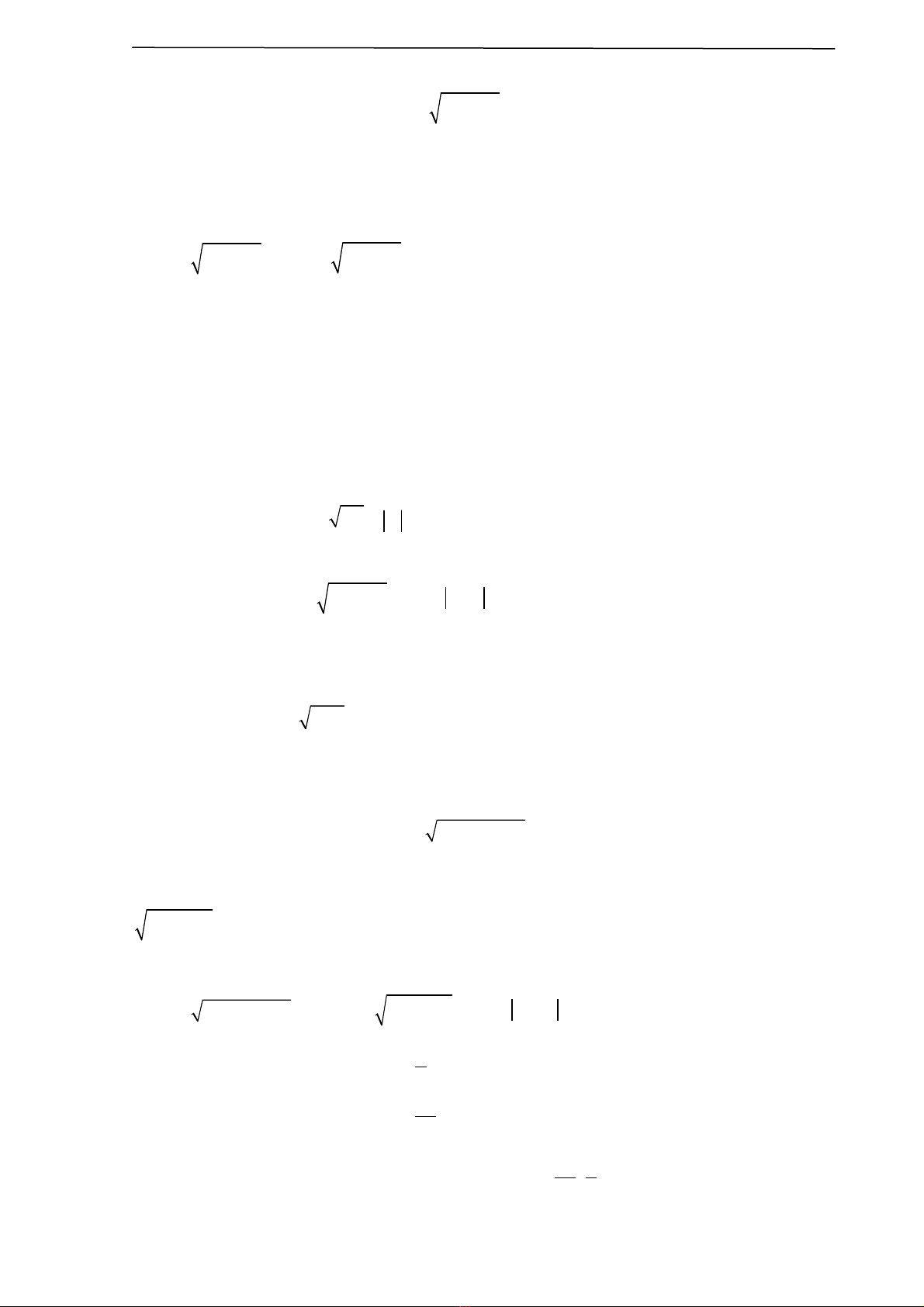
M t s gi i pháp v gi i ph ng trình vô t dành cho h c sinh gi i l p 9 tr ng THCS Lê Đình ộ ố ả ề ả ươ ỉ ọ ỏ ớ ườ
Chinh
Ví d 2.ụ Gi i ph ng trình: ả ươ
( )
2
x 3 9− =
Phân tích: Ph ng trình đã cho ph i là ph ng trình d ng 1 ch a? Nêu cáchươ ả ươ ạ ư
gi i.ả
Gi iả
Ta có:
( )
2
x 3 9− =
( )
( )
2
22
x 3 9 − =
( )
2
x 3 81 − =
2
x 6x 9 81 − + =
2
x 6x - 72 = 0 −
2
x 12x 6x 72 0 − + − =
( )
( )
2
x 12x 6x 72 0 − + − =
x(x 12) 6(x 12) 0 − + − =
(x 12)(x 6) 0 − + =
x 12 0
x 6 0
− =
+ =
x 12
x 6
=
= −
V y t p nghi m c a ph ng trình đã cho là: S = ậ ậ ệ ủ ươ
{ }
6;12−
Giáo viên? Ngoài cách gi i trên còn cách gi i nào khác không? (B d u cănả ả ỏ ấ
b c hai theo ki n th c ậ ế ứ
2
A A=
r i gi i ph ng trình ch a d u giá tr tuy t đi đaồ ả ươ ứ ấ ị ệ ố
h c)ọ
Cách 2. Ta có:
( )
2
x 3 9− =
x 3 9 − =
x 3 9
x 3 9
− =
− = −
x 12
x 6
=
= −
V y t p nghi m c a ph ng trình đã cho là: S = ậ ậ ệ ủ ươ
{ }
6;12−
Nh n xét:ậ Giáo viên cho h c sinh nh n xét v hai cách gi i trên? Khi nào thìọ ậ ề ả
ph ng trình d ng ươ ạ
f (x) m=
gi i đc theo cách 2? T đó ch n cách gi i phù h pả ượ ừ ọ ả ợ
cho t ng bài toán. (Cách 2 gi i đn gi n h n cách 1, đ bài toán gi i đc theo cáchừ ả ơ ả ơ ể ả ượ
2 thì bi u th c d i d u căn vi t đc d i d ng bình ph ng c a m t bi u th cể ứ ướ ấ ế ượ ướ ạ ươ ủ ộ ể ứ
n u không thì gi i theo cách 1)ế ả
Ví d 3:ụ Gi i ph ng trình ả ươ
2
4x 4x 1 6 0− + − =
Phân tích: Ph ng trình đã cho có th đa v d ng c a ph ng trình ví d 2 trangươ ể ư ề ạ ủ ươ ụ
5 đc không? (H c sinh nêu cách bi n đi ph ng trình đã cho v d ngượ ọ ế ổ ươ ề ạ
( )
2
2x 1 6− =
)
Gi iả
Ta có:
2
4x 4x 1 6 0− + − =
( )
2
2x 1 6 − =
2x 1 6 − =
2x 1 6
2x 1 6
− =
− = −
2x 7
2x 5
=
= −
7
x2
5
x2
=
−
=
V y t p nghi m c a ph ng trình đã cho là: S = ậ ậ ệ ủ ươ
5 7
;
2 2
−
.
�
Trang 5


























