LUYỆN TẬP 2
A. MỤC TIÊU
Rèn kĩ năng chứng minh hai tam giác vuông bằng nhau nhờ áp dụng các trường
hợp bằng nhau c.g.c ; g.c.g của hai tam giác, áp dụng hai hệ quả của trường hợp
bằng nhau g.c.g.
Rèn kĩ năng vẽ hình, viết giả thiết, kết luận, chứng minh.
B. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH
GV: Thước thẳng, êke vuông, bảng phụ, bút dạ
HS: Thước thẳng, êke vuông.
C. TIẾN TRÌNH DẠY HỌC
Hoạt động của GV Hoạt động của HS
Hoạt động 1 : KIỂM TRA
Đề bài viết trên bảng phụ
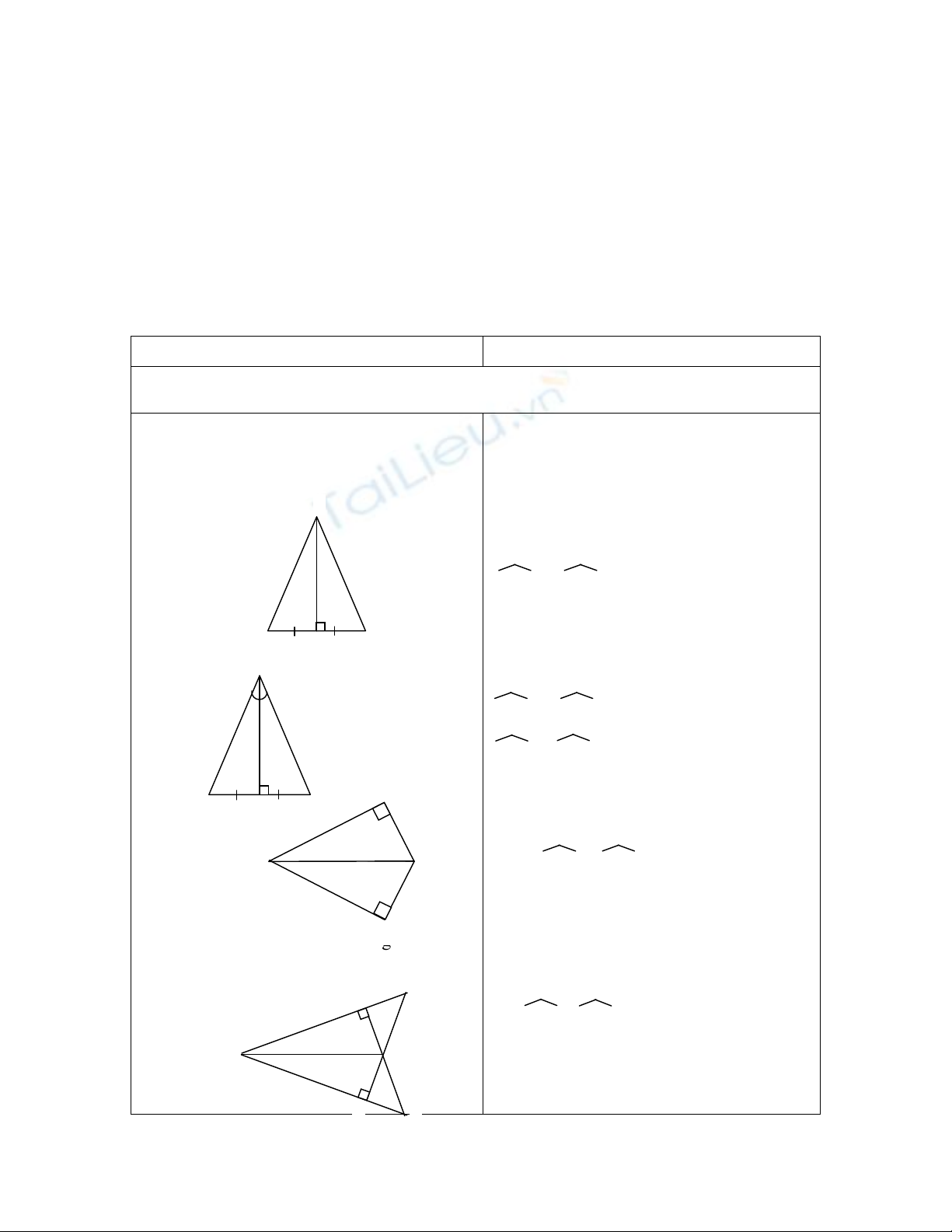
HS1: Chữa bài tập 39 Tr 124 SGK.
Trên mỗi hình có các tam giác vuông nào
bằng nhau ?
HS1 trả lời miệng
Hình 105
- Theo hình 105 có:
AHB = AHC (c.g.c) vì có
BH = CH (gt);
AHB = AHC (= 900);
AH chung
Hình 106
- Theo hình 106 có:
EDK = FDK (g.c.g) vì có:
EDK = FDK (gt);
cạnh DK chung
DKE = DKF (= 900)
Hình 107
- Theo hình 107 có:
vuông ABD = vuông ACD
(cạnh huyền – góc nhọn).
Vì có BAD = CAD (gt)
cạnh huyền AD chung.
HS2: Chỉ ra các tam giác bằng nhau trên
hình sau:
HS2 làm trên bảng
- ABD = ACD vì
B
ˆ = C
ˆ
= 900
và BAD = CAD (gt)
cạnh huyền AD chung
(theo TH cạnh huyền – góc nhọn)
BED = CHD vì
B
ˆ = C
ˆ
= 900; 1
ˆ
D
= 2
ˆ
D
(đối đỉnh)
Ti
ế
t 34
A
B
C
H
D
E
F
A
B
C
D
A
B
C
D
E
H
1
2
Hình 108 BD = CD (do ABD = ACD chứng
minh trên ) (theo TH g.c.g).
- GV đánh giá, cho điểm hai HS lên bảng.
- ADE = ADH vì
cạnh AD chung
DE = DH (do BED = CHD)
AE = AH (= AB + BE = AC + CH)
(theo TH c.c.c)
HS lớp nhận xét bài làm của bạn
Hoạt động 2
LUYỆN TẬP
Bài 62 Tr 105 SBT
(Đề bài đưa lên màn hình)
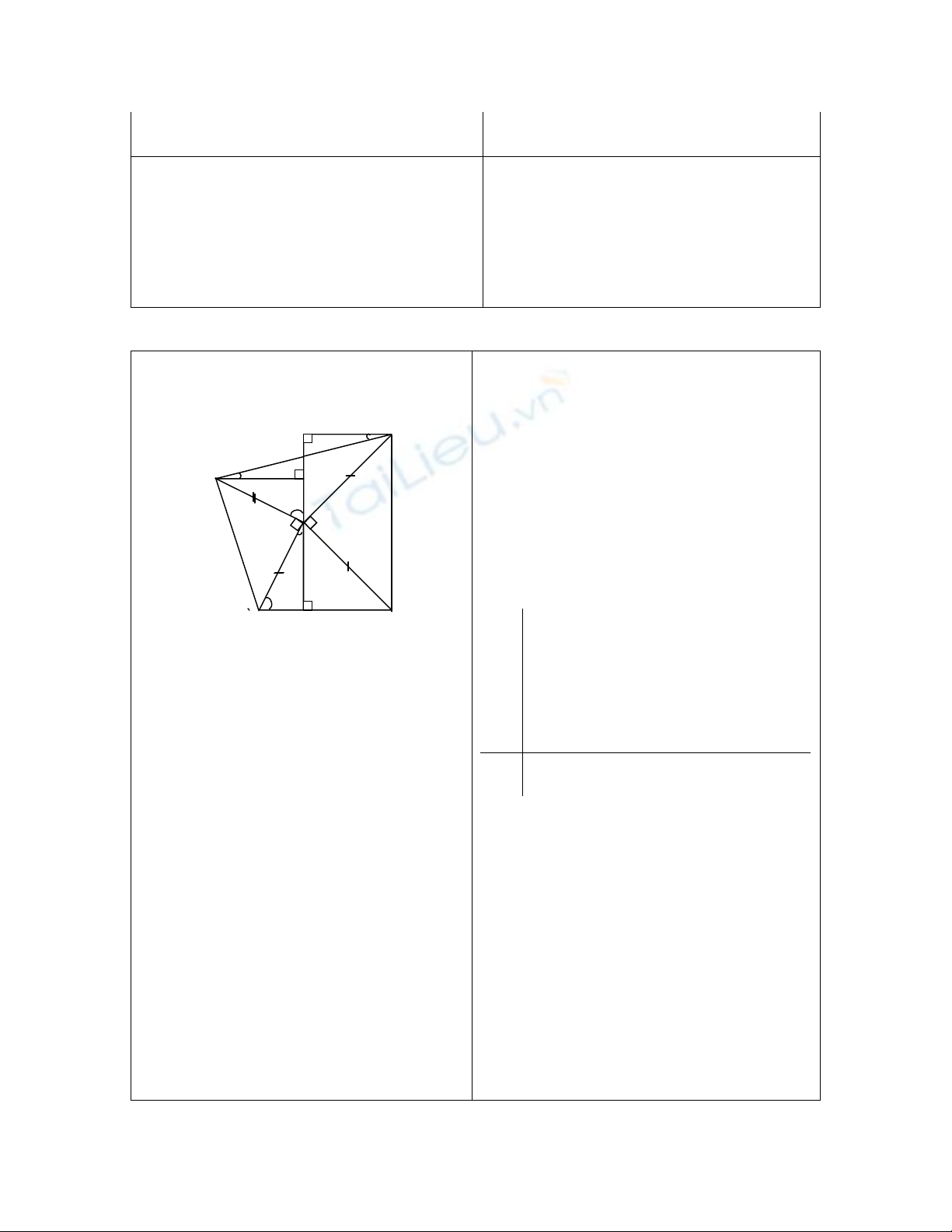
GV vẽ hình và hướng dẫn
HS vẽ hình và kí hiệu trên hình
Sau đó yêu cầu HS nêu GT, KL của bài
toán. GT
ABC
ABD:
A
ˆ = 900, AD = AB
ACE:
A
ˆ = 900, AE = AC
AH BC, DM AH.
EN AH
DE MN = {O}
KL
DM = AH
OD = OE
- Để có DM = AH ta cần chỉ ra 2 tam giác
nào bằng nhau ? a) Xét DMA và AHB có:
M
ˆ =
H
ˆ = 900 (gt);
AD = AB (gt)
1
ˆ
A
+ 2
ˆ
A
= 1800 - 3
ˆ
A = 1800 - 900 = 900
1
ˆ
B
+ 2
ˆ
A
= 900
1
ˆ
A
= 1
ˆ
B
(cùng phụ với 2
ˆ
A
)
DMA = AHB (cạnh huyền-góc
nhọn)
DM = AH (cạnh tương ứng)
- Tương tự có 2 tam giác nào bằng nhau để
được NE = AH ? b) Chứng minh tương tự ta có
NEA = HAC
NE = AH (cạnh tương ứng)
theo chứng minh trên ta có:
B
H
C
A
E
N
D
M
O1
1
22
1
1
3
DM = AH ; NE = AH
DM = NE
mà NE AH, DM AH
NE // DM
1
ˆ
D
= 1
ˆ
E
(2 góc so le trong)
có 1
ˆ
N = 1
ˆ
M
= 900
DMO = ENO (g.c.g)
OD = OE (cạnh tương ứng) hay MN đi
qua trung điểm O của DE
- GV có thể bổ sung thêm câu hỏi (nếu còn
thời gian).
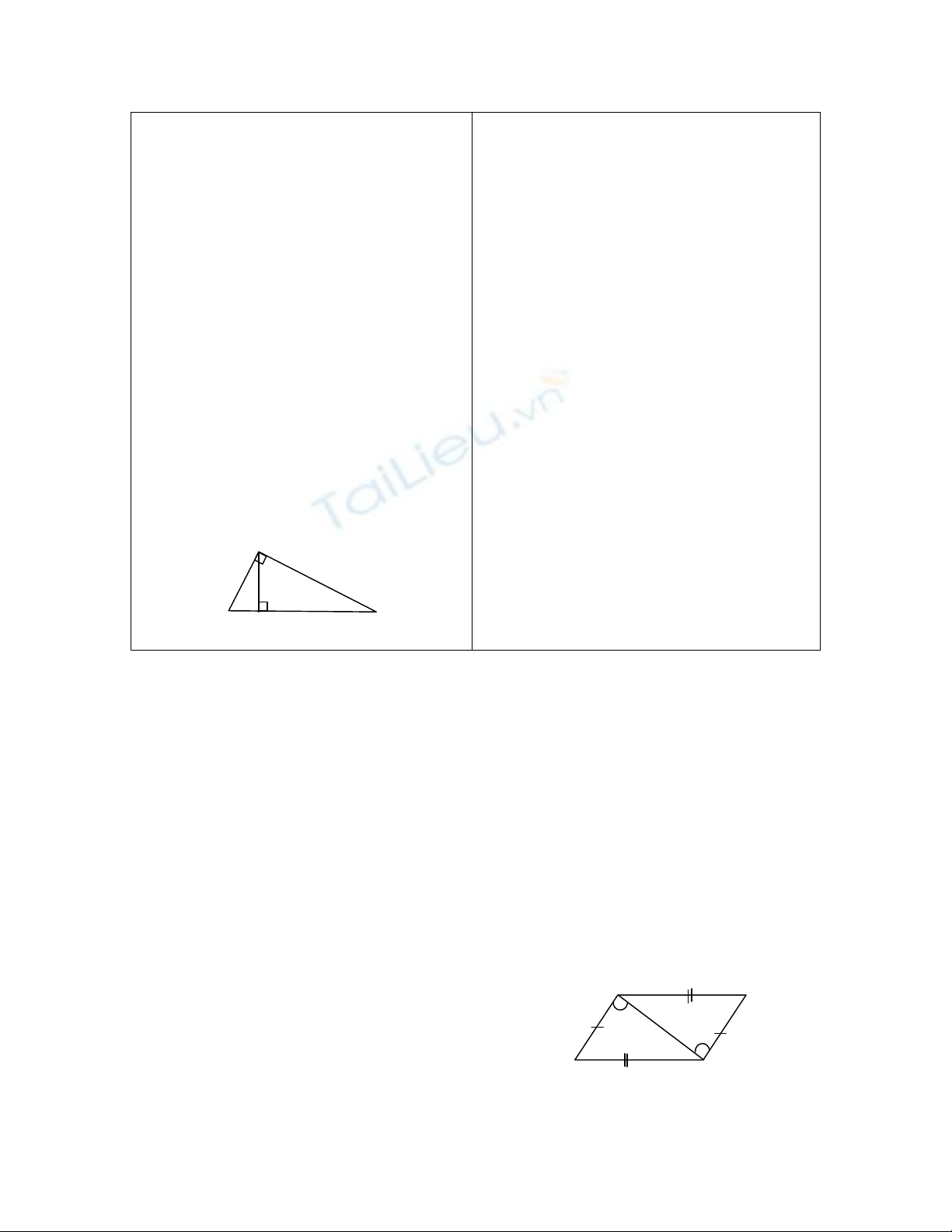
Nếu ABC có
A
ˆ = 900. Hãy xét xem
ABC và AHC có những yếu tố nào
bằng nhau hay không ?
GV đưa hình vẽ sẵn lên màn hình máy
chiếu (có thể cho HS thảo luận nhóm)
HS phát biểu:
ABC có
A
ˆ = 900
AHC có
H
ˆ = 900
A
ˆ =
H
ˆ = 900
có góc C, cạnh AC chung.
ABC và AHC có 2 góc bằng nhau
không thỏa mãn điều kiện 2 góc kề với một
cạnh tương ứng bằng nhau (theo g.c.g) nên
2 tam giác không bằng nhau.
Hoạt động 3
DẶN DÒ
- Ôn tập kĩ lí thuyết về các trường hợp bằng nhau của tam giác.
Làm các bài tập 57, 58, 59, 60, 61 Tr 105 SBT.
Hoạt động 4
KIỂM TRA GIẤY
Câu 1: Các khẳng định sau đúng hay sai ?
1. ABC và DEF có AB = DF, AC = DE, BC = FE
thì ABC = DEF (theo trường hợp c.c.c)
2. MNI và M’N’I’ có
M
ˆ =
'
ˆ
M
,
I
ˆ =
'
ˆ
I
, MI = M’I’
thì MNI = M’N’I’ (theo trường hợp g.c.g)
Câu 2: Cho hình vẽ bên có
AB = CD ; AD = BC ; 1
ˆ
A
= 850
a) Chứng minh ABC = CDA
b) Tính số đo của 1
ˆ
C
c) Chứng minh AB // CD
B
A
C
H
1
1
2
2
A
D
B
C
LUYỆN TẬP 3
A. MỤC TIÊU
Luyện kĩ năng chứng minh hai tam giác bằng nhau theo cả ba trường hợp của tam
giác thường và các trường hợp áp dụng vào tam giác vuông.
Kiểm tra kĩ năng vẽ hình, chứng minh hai tam giác bằng nhau.
B. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH
GV: Thước thẳng, phấn màu, thước đo độ.
HS: Thước thẳng, thước đo độ.
C. TIẾN TRÌNH DẠY HỌC
Hoạt động của GV Hoạt động của HS
Hoạt động 1
KIỂM TRA KẾT HỢP LUYỆN TẬP
GV: Nêu câu hỏi kiểm tra.
- Cho ABC và A’B’C’, nêu điều kiện
cần có để hai tam giác trên bằng nhau theo
các trường hợp c.c.c ; c.g.c ; g.c.g ?
HS lớp ghi câu trả lời vào nháp.
Một HS lên bảng trình bày
ABC và A’B’C’ có
1) AB = A’B’
AC = A’C’
BC = B’C’
ABC = A’B’C’ (c.c.c)
2) AB = A’B’
B
ˆ =
'
ˆ
B
BC = B’C’ (c.g.c)
ABC = A’B’C’ (c-g-c)
3)
A
ˆ =
'
ˆ
A
AB = A’B’ ;
B
ˆ =
'
ˆ
B
ABC = A’B’C’ (g.c.g)
(HS có thể ghi các cạnh, góc khác nhưng
phải đúng)
GV: Đưa đề bài lên màn hình
Bài tập 1:
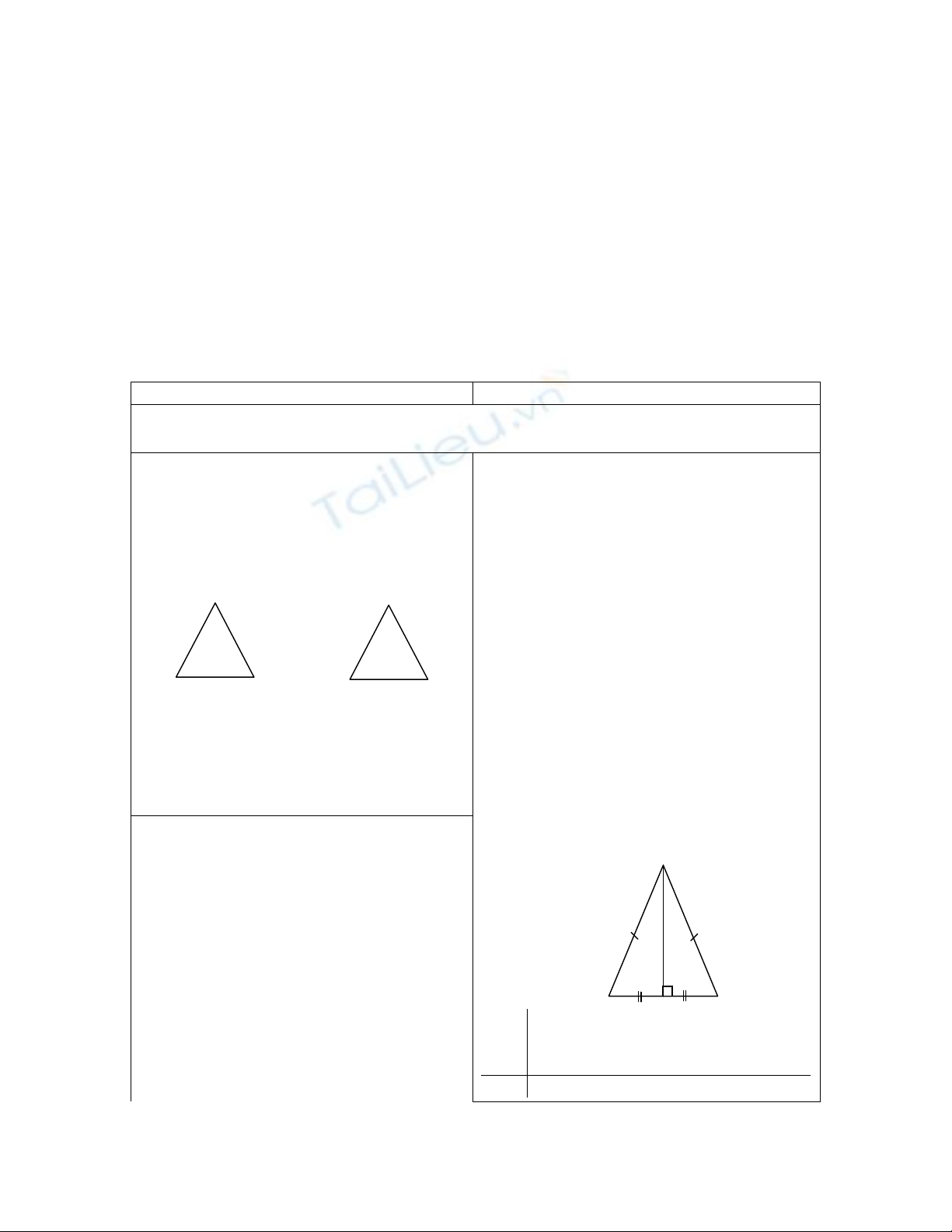
a) Cho ABC có AB = AC, M là trung
điểm BC.
Chứng minh AM là phân giác góc A
b) Cho ABC có
B
ˆ = C
ˆ
, phân giác góc
A cắt BC ở D. Chứng minh rằng AB = AC.
GV: Yêu cầu HS vẽ hình ghi GT, KL và
chứng minh.
- GV: Có thể cho HS làm theo thứ tự:
Dãy 1: 2 làm câu a trước, câu b sau
Dãy 3: 4 làm câu b trước, câu a sau
Gọi hai HS lên bảng vẽ và làm trên bảng,
HS: Làm theo hướng dẫn của GV
a)
GT ABC có:
AB = AC
MB = MC
KL AM là phân giác góc A
Ti
ế
t 35
C’’
B’
A’
C
B
A
A
B
C
M
sau đó đánh giá cho điểm.
Xét ABM và ACM có
AB = AC (gt)
BM = MC (vì M là trung điểm của BC),
cạnh AM chung.
ABM = ACM (góc tương ứng)
AM là phân giác góc A.
b)
GT
ABC có:
B
ˆ = C
ˆ
, 1
ˆ
A
= 2
ˆ
A
KL
AB = AC
Xét ABD và ACD có
1
ˆ
A
= 2
ˆ
A
(gt) (1)
B
ˆ = C
ˆ
(gt)
1
ˆ
D
= 1800 – (
B
ˆ + 1
ˆ
A
)
2
ˆ
D
= 1800 – (C
ˆ
+ 2
ˆ
A
)
1
ˆ
D
= 2
ˆ
D
(2)
cạnh DA chung (3)
Từ (1), (2), (3) ta có
ABD = ACD (g.c.g)
AB = AC (cạnh tương ứng)
Hoạt động 2
LUYỆN TẬP
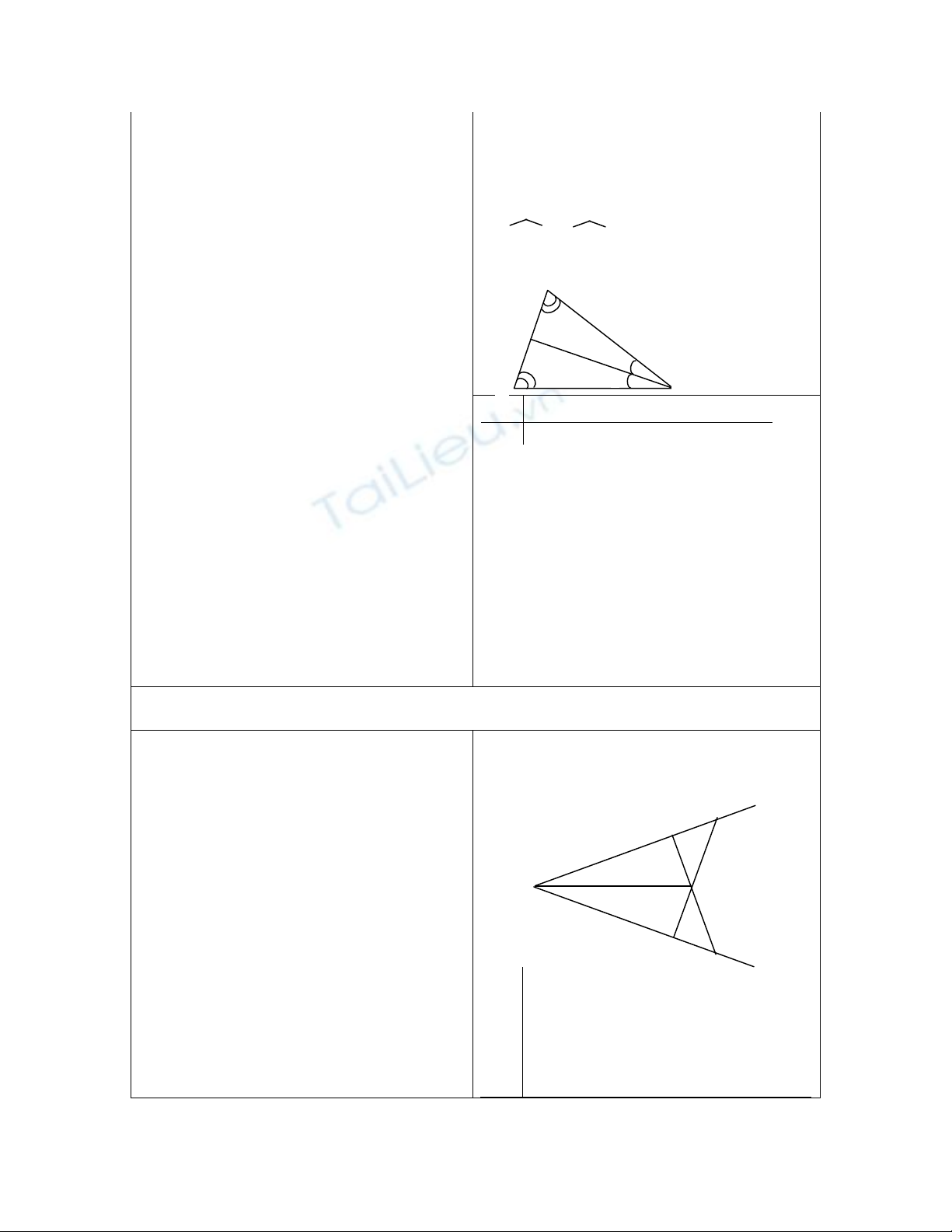
Bài tập 2: (bài 43 Tr 125 SGK)
(Đề bài đưa lên màn hình) Một HS đọc to đề bài
Một HS vẽ hình và viết GT, KL trên bảng
GT
Góc xOy khác góc bẹt
A: B thuộc tia Ox
OA < OB
C ; D thuộc tia Oy
OC = OA ; OD = OB
AD BC = {E}
B
1
2
A
C
D
1
2
O
A
C
E
y
1
2
1
1
1
1
B
D
2
2
x


























