TIẾT 36: LUYỆN TẬP
I. Mục tiêu:
- Giúp học sinh củng cố khái niệm cân, đều, vận dụng tính chất cân, đều để nhận
biết các loại đó và để tính số đo góc, để cm các góc bằng nhau, các đoạn thẳng bằng nhau
hay song song.
- Rèn kĩ năng vẽ hình, viết GT, KL, tập suy luận chứng minh bài toán.
II. Chuẩn bị của G và H:
Giáo viên : Thước thẳng, thước đo góc, com pa.
Học sinh : Thước thẳng, thước đo góc, com pa, bút chì.
III. Tiến trình bài dạy:
1. Kiểm tra bài cũ- đặt vấn đề chuyển tiếp vào bài mới: (3’- 5’)
H1: Phát biểu định nghĩa, t/c của tam giác cân, định nghĩa và t/c của tam giác vuông cân.
Vẽ hình minh họa.
- H2: Phát biểu định nghĩa, t/c của tam giác đều, Vẽ hình minh họa. Điều kiện để tam giác
cân trở thành tam giác vuông cân, tam giác đều
2. Dạy học bài mới:
HOẠT ĐỘNG CỦA THẦY HOẠT ĐỘNG CỦA TRÒ NỘI DUNG GHI BẢNG
HOẠT ĐỘNG 1: CHỮA BÀI VỀ NHÀ (10’ – 12’)
Bài 46 ( Tr 127- SGK)
Yêu cầu học sinh lên bảng
chữa
+ Yêu cầu hs nêu rõ từng bước
vẽ
Bài 49 ( Tr 127- SGK)
+ Chốt: Tính góc ở đáy của tam
giác cân biết góc ở đỉnh ta làm
như thế nào?
Tính góc ở đỉnh của
tam giác cân biết góc ở đáy ta
làm như thế nào?
+ 1hs lên bảng làm
+ Vẽ đoạn BC = 3cm.
+ Vẽ hai cung tròn
tâm B, C có cùng bán
kính 4cm. Hai cung
tròn cắt nhau tại A
+ Nối A với B, A với
C ta được tam giác
cân ABC ( cân tại A)
Một học sinh lên
bảng
làm bài.
+ Góc ở đáy = (1800 -
góc ở đỉnh): 2
+ Góc ở đỉnh = 1800 -
2 lần góc ở đáy
I. Chữa bài tập:
Bài 46 (Tr 127- SGK)
Bài 49 ( Tr 127- SGK)
a) Xét tam giác ABC có :
A
ˆ +
B
ˆ + C
ˆ = 1800 (định lý
tổng ba góc của )
B
ˆ + C
ˆ = 1800 -
A
ˆ
B
ˆ + C
ˆ = 1800 - 400 (
A
ˆ= 400
(GT))
B
ˆ + C
ˆ = 1400
Mà
B
ˆ = C
ˆ
(t/c tam giác cân)
B
ˆ = C
ˆ = 1400 : 2
B
ˆ = C
ˆ = 700
b) Xét tam giác ABC có :
B
C
40
0
A
A
B
40
0
A
ˆ +
B
ˆ + C
ˆ
= 1800 (định lý
tổng ba góc của )
A
ˆ= 1800 - (
B
ˆ + C
ˆ )
Mà
B
ˆ = C
ˆ= 400 (t/c tam giác
cân)
B
ˆ + C
ˆ = 800
A
ˆ= 1800 - 800
A
ˆ = 1000
HOẠT ĐỘNG 2: LUYỆN TẬP (18’ – 20’)
Bài 50 ( Tr 127- SGK)
Yêu cầu học sinh đọc đề bài,
vẽ hình, ghi GT, KL, nêu
hướng cm bài toán-> trình bày
lời giải
Chữa bài làm của học sinh,
hoàn thiện lời giải mẫu.
Bài 51 ( Tr 127- SGK)
Bằng trực giác ta thấy số đo của
hai góc?
Để cm điều này cân gắn vào việc
cm 2 nào bằng nhau? để cm hai
tg đó bằng nhau cần chỉ ra các
Một học sinh lên
bảng làm bài, cả
lớp làm vào vở.
Nhận xét bổ sung
lời giải của bạn.
+ Một học sinh lên
bảng vẽ hình, ghi GT,
KL, cả lớp làm vào
vở.
II. Luyện tập:
a) Xét tam giác ABC có :
A
ˆ +
B
ˆ + C
ˆ
= 1800 (định lý
tổng ba góc của )
B
ˆ + C
ˆ = 1800 -
A
ˆ
B
ˆ + C
ˆ = 1800 - 1450 (
A
ˆ=
1450 (GT))
B
ˆ + C
ˆ = 350
Mà
B
ˆ = C
ˆ (t/c tam giác cân)
B
ˆ = C
ˆ
= 350 : 2
B
ˆ = C
ˆ = 17,50
b) Tương tự ta tính được
B
ˆ = C
ˆ = 400
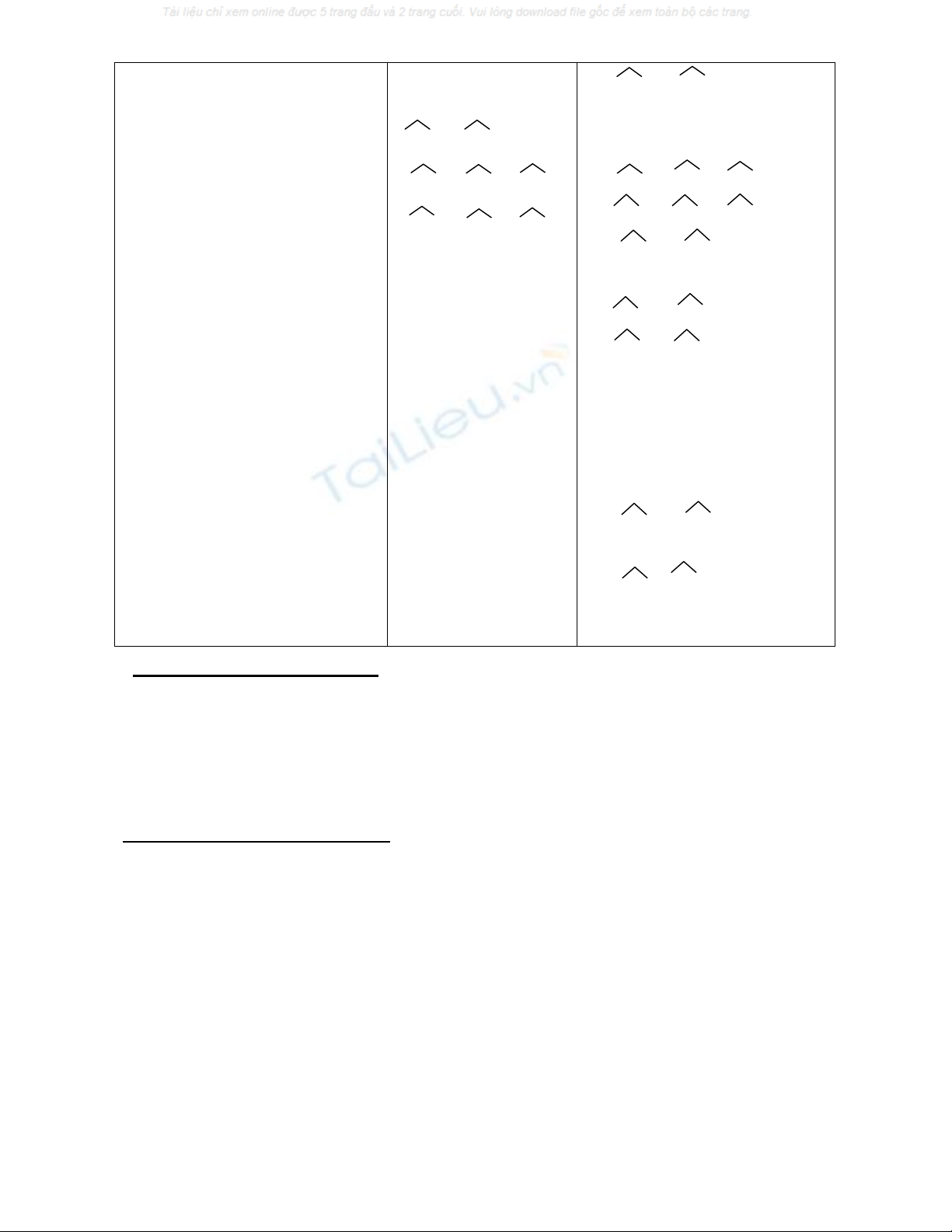
Bài 51 ( Tr 127- SGK)
Chứng minh:
Xét ABD và ACE có :
AB = AC (Do ABC cân tại
A theo GT)
 : góc chung
AD = AE (GT)
ABD = ACE (c.g.c) (1)
A
B
C
A
B C
D
E I
GT
ABC cân tại A
D AC; E AB
AD = AE
BD CE = {I}
KL a) ss: ABD và ACE
b) IBC là gì?
ABD = ACE
ABD = ACE
?
yếu tố nào bằng nhau?
b) Dự đoán IBC là tam giác gì?
hãy đưa ra các lí do để chứng
minh điều đó.
Chốt : khi cm 2 tam giác bằng
nhau cần lựa chọn xem nên cm
theo trường hợp nào ? muốn vậy
cần dựa vào GT và kết quả cm ở
các câu trước.
Một học sinh lên bảng
làm bài, cả lớp làm
vào vở.
Nhận xét bổ sung lời
giải của bạn.
ABD = ACE (hai góc tương
ứng)
b) Ta có :
DBC = ABC - ABD
ECB = ACB - ACE
Mà ABC = ACB (tc ABC cân
tại A )
ABD = ACE (CM)
DBC = ECB
IBC cân tại I
c) C/m IBE = ICD
Xét IBE và ICD
IB = IC (tc IBC cân tại I)
EIB = DIC (hai góc đối
đỉnh)
IBE = ICD (cmt)
IBE = ICD (g.c.g)
3. Luyện tập và củng cố bài học: (5’ – 6’)
- Yêu cầu hs đọc phần đọc thêm: giới thiệu định lí thuận, đảo. hai định lí như thế nào được
gọi là 2 định lí thuận đảo của nhau.
- Yêu cầu hs lấy ví dụ định lí thuận, đảo
- Lưu ý cho hs ko phải định lí nào cũng có định lí đảo.
4. Hướng dẫn học sinh học ở nhà: (2’)
- Nắm vững : DDN, T/c của cân, vuông cân, đều
- Cách nhận biết cân, vuông cân, đều
- Bài tập 52 (Tr 128 - SGK). Bài tập 68 đến 71 (Tr 106 - SBT tập 1)
IBC cân tại I
DBC = ECB
DBC = ABC - ABD
ECB = ACB
-
ACE
Ngày soạn:31/1/2007 Ngày giảng: 03/02/2007
TIẾT 37: ĐỊNH LÍ PI-TA-GO
I. Mục tiêu:
- Giúp học sinh nắm được định lý Pitago về quan hệ giữa ba cạnh của tam giác vuông, biết
vận dụng định lý Pitago để cm cạnh huyền, cạnh góc vuông của hai tam giác vuông.
- Biết vận dụng định lý Pitago để tính độ dài một cạnh của tam giác vuông khi biết độ dài
của hai cạnh kia.
- Biết cm hai tam giác vuông bằng nahu theo trường hợp cạnh huyền, cạnh góc vuông.
- Biết vận dụng các kiến thức học trong bài vào các bài toán thực tế.
II. Chuẩn bị của G và H:
Giáo viên: Thước thẳng, êke, com pa..
Học sinh: Thước thẳng, Eke, com pa, bút chì.
III. Tiến trình bài dạy:
1. Kiểm tra bài cũ- đặt vấn đề chuyển tiếp vào bài mới: (3’)
Kiểm tra sự chuẩn bị của HS
2. Dạy học bài mới:
HOẠT ĐỘNG CỦA THẦY HOẠT ĐỘNG CỦA TRÒ NỘI DUNG GHI BẢNG
HOẠT ĐỘNG 1: ĐỊNH LÝ PITAGO (18’ – 20’)
Yêu cầu học sinh làm ?1 vẽ
một tam giác vuông có các
cạnh góc vuông là 3cm, 4cm.
Đo độ dài cạnh huyền của tam
giác vuông đó?
+ Yêu cầu học sinh làm ?2 :
Tính dt hình vuông 1 (có
cạnh là c)
Tính dt hình vuông 2 (có
cạnh là a)
Tính dt hình vuông 3 (có
cạnh là b)
So sánh dt hình vuông 1
với dt hình vuông 2 và 3.
Rút ra nhận xét gì về quan hệ
giữa c2 với a2 + b2 , Nhận xét
về quan hệ giữa ba cạnh của
tg vuông.
Giới thiệu định lý Pitago
Cả lớp đo rồi trả lời
?1 (SGK/129)
ABC vuông tại A
AB= 3cm; AC =
4cm
Đo BC = 5cm
+ dt hv1 = c2
+ dt hv1 = a2
+ dt hv1 = b2
+ c2 = a2 + b2
1. Định lý Pitago
Định lý Pitago: (SGK/130)
ABC vuông tại A
BC2 = AB2 + AC2
Lưu ý : Gọi bình phương độ dài
đoạn thẳng là bình phương của
đoạn thẳng đó.
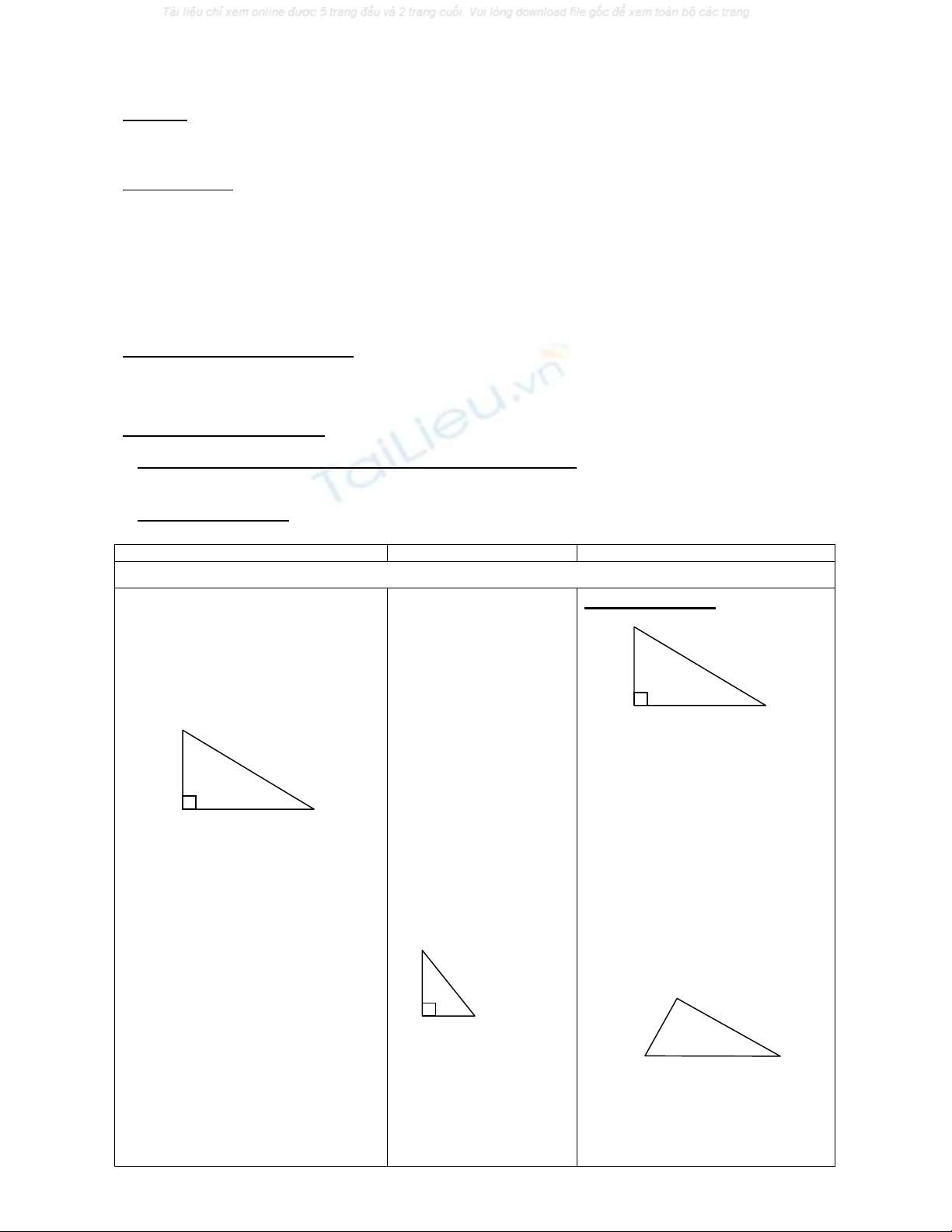
Áp dụng ? 3 ( SGK/130)
a) hình 124
Vì ABC vuông tại B
AC2 = AB2 + BC2 (đl
pitago)
b
a
c
A
B
C
8
10
3
B
C
4
A
C
A
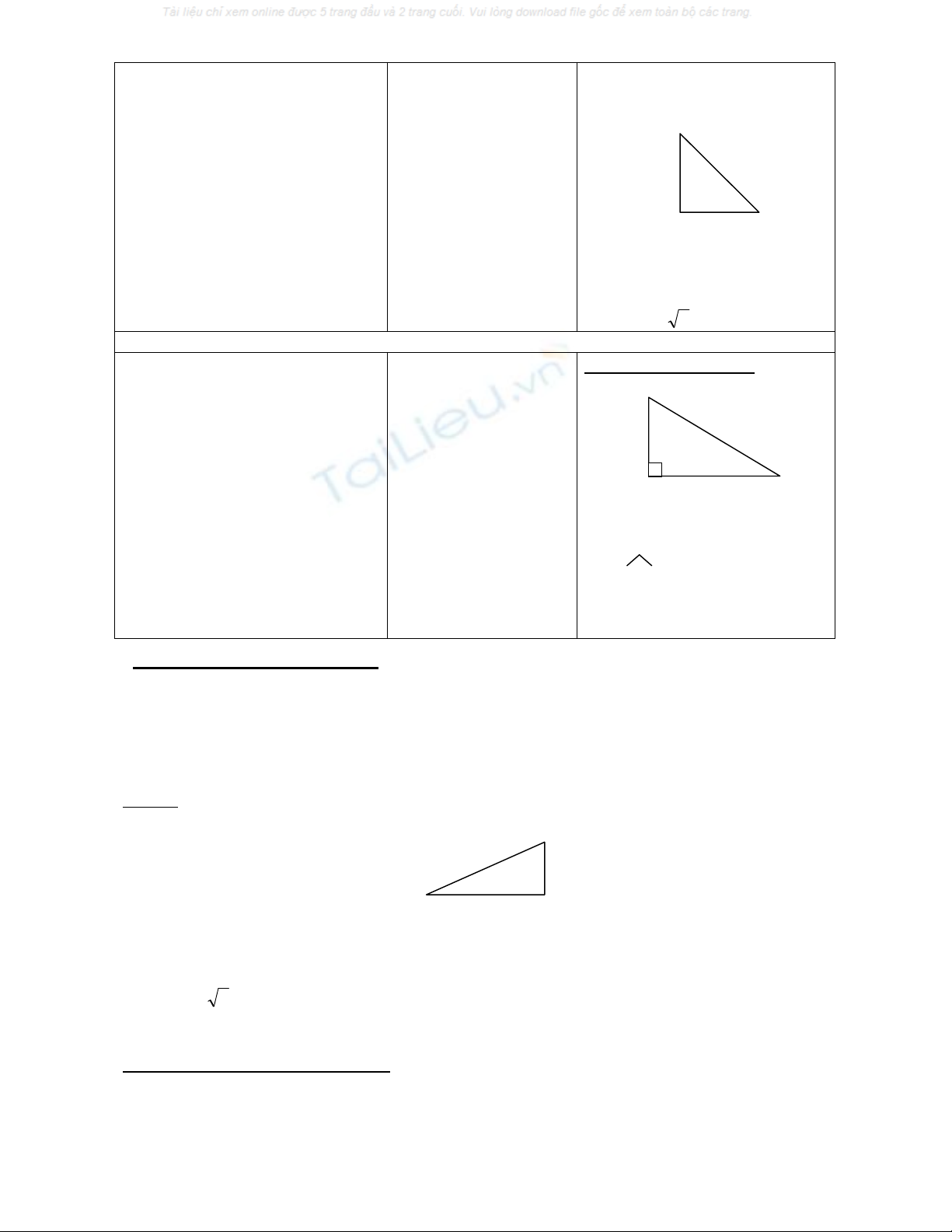
Yêu cầu học sinh làm ?3
+ Cả lớp làm ?3
Nêu kết quả.
102 = x2 + 82
x2 = 36 x = 6
b) hình 125
Vì DEF vuông tại D
EF2 = ED2 + DF2 (đl pitago)
x2 = 12 + 12 =2
x = 2
HOẠT ĐỘNG 2: ĐỊNH LÝ PITAGO ĐẢO(6’ – 8’)
Yêu cầu học sinh làm ?4
(30/SGK)
+ Rút ra định lý
Cả lớp làm ?4
Nêu kết quả.
?4
ABC có AB = 3cm
AC = 4cm; BC =
5cm
Đo góc BAC = 900
Phát biểu định lý
Pitago đảo
2. Định lý Pitago đảo
Định lý Pitago đảo: SGK/130
ABC: BC2 = AB2 + AC2
BAC = 900
3. Luyện tập và củng cố bài học: (10’ – 12’)
- Bài học hôm nay cần nắm những vấn đề gì? Phát biểu 2 định lý thuận.
- Định lý đảo – so sánh hai định lý.
- Yêu Cầu hs làm bài tập 53/131SGK ( 2 hs lên bảng làm, cả lớp làm vào vở)
Bài 53 (Tr 131 - SGK)
a) Vì DEF vuông tại D
EF2 = ED2 + DF2 (đl Pitago)
x2 = 122 + 52
x = 144 + 25 =169
x = 13
d) x2 =
2
7+ 32 = 7 + 9
x2 = 16 x = 4
4. Hướng dẫn học sinh học ở nhà: (2’)
- Học kĩ định lý Pitago, định lý đảo, đọc mục có thể em chưa biết.
- Bài tập 53 đến 56 (Tr 131 - SGK).
E
D
F
1
1
x
3
B
C
4
A
x
5
12
D
E
F


























