78
Chƣơng 5
CÁC ĐỊNH LÝ GIỚI HẠN
5.1. ĐỊNH NGHĨA. Dãy các ĐLNN {Xn} đƣợc gọi là hội tụ theo
xác suất tới ĐLNN X nếu với
> 0,
n
n
limP X X 1.
 

Khi đó
ta ký hiệu:
P
n
XX
.
5.2. BẤT ĐẲNG THỨC TRÊ-BƢ-SÉP. Cho ĐLNN X có kỳ
vọng E(X) và phƣơng sai D(X) đều hữu hạn. Khi đó với mọi  > 0,
ta có:
22
D(X) D(X)
P X E(X) 1 hay P X E(X)

(1)
Các bất đẳng thức (1) đƣợc gọi là các bất đẳng thức Trê-bư-sép.
Chứng minh: Giả sử X là ĐLNN liên tục có hàm mật độ phân phối
f(t).
Theo tính chất hàm mật độ, ta có:
E(X)
E(X)
P X E(X) P E(X) X E(X) f (t)dt


E(X)
E(X)
1 f (t)dt f (t)dt
 
 





. (2)
Mặt khác:
2
22
2
t E(X)
t E(X) t E(X) 1
2
2
t E(X)
f (t). f (t)

(vì f(t) 0).
Vì f(t) 0 nên
E(X)
E(X)
f (t)dt f (t)dt f (t)dt
  
 

E(X)
2
E(X)
1
f (t)dt f (t)dt .D(X)
 
 

(3)
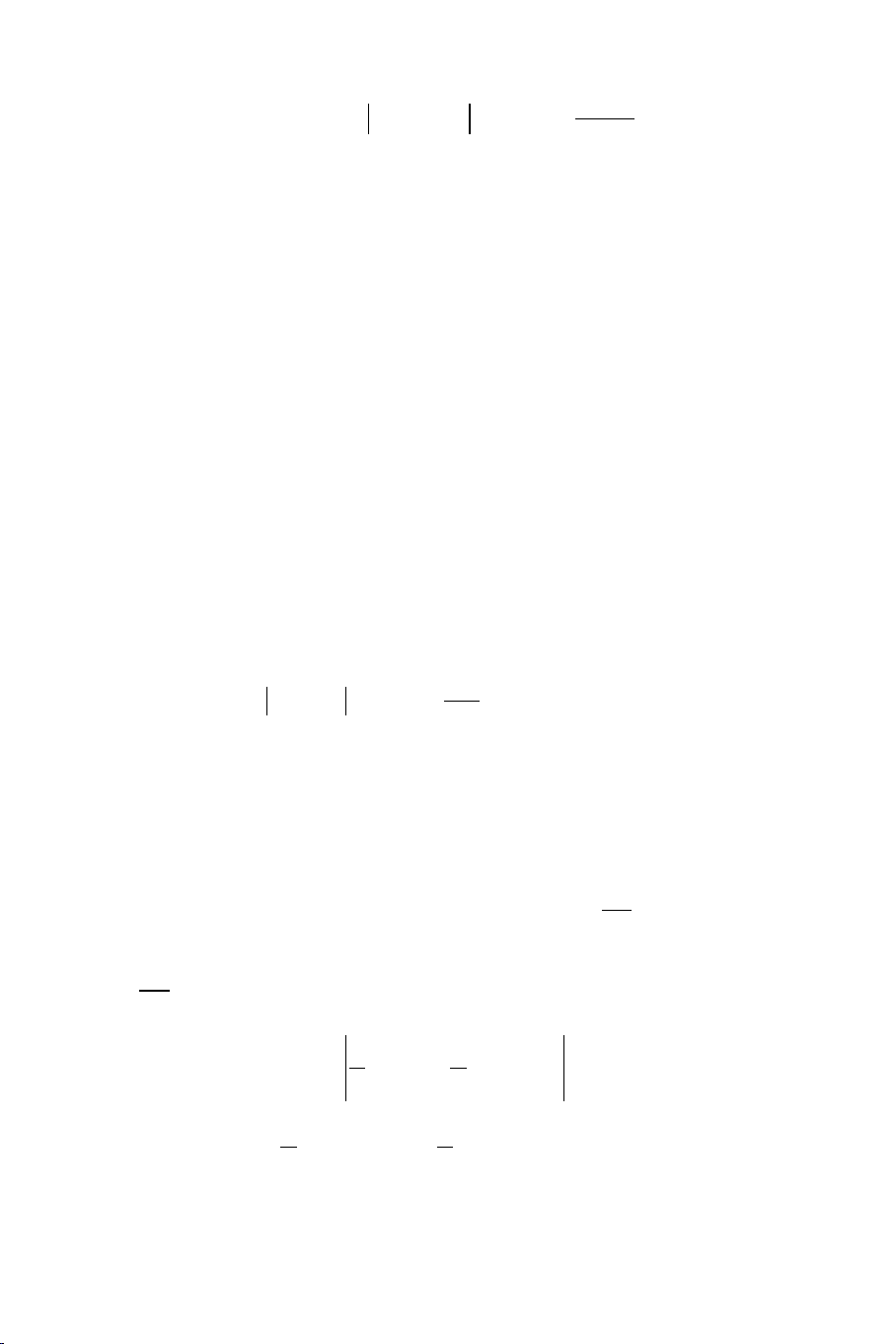
79
Từ (2) và (3) suy ra:
2
D(X)
P X E(X) 1 .
฀
Về mặt thực tế bất đẳng thức Trê-bƣ-sép chỉ cho phép đánh giá
cận trên hoặc cận dƣới xác suất để ĐLNN X nhận giá trị sai lệch so
với kỳ vọng của nó lớn hơn hoặc bé thua . Đôi khi sự đánh giá đó là
hiển nhiên và không có ý nghĩa. Chẳng hạn, nếu D(X) 2 thì bất
đẳng thức là hiển nhiên đúng. Song nó lại có ƣu điểm là áp dụng đƣợc
đối với mọi ĐLNN mà không cần biết quy luật phân phối xác suất của
nó.
Ví dụ 1. Thu nhập trung bình hàng năm của dân cƣ một vùng là
700 USD và độ lệch chuẩn là 120 USD. Hãy xác định một khoảng thu
nhập hàng năm xung quanh giá trị trung bình của ít nhất 95% dân cƣ
vùng đó.
Giải. Gọi X là thu nhập hàng năm của dân cƣ vùng đó thì X là
ĐLNN với quy luật phân phối xác suất chƣa biết song có kỳ vọng toán
E(X) = 700 và độ lệch chuẩn D(X) = 120. Do đó theo bất đẳng thức
Trê-bƣ-sép, ta có:
2
130
P X 700 1 0,95 536,656
Vậy ít nhất 95% dân cƣ vùng đó có thu nhập hàng năm nằm trong
khoảng (700 – 536,656; 700 + 536,656), tức là khoảng (163,344;
1236,656).
5.3. ĐỊNH LÝ TRÊ-BƢ-SÉP
5.3.1. Định lý. Giả sử X1, X2, ..., Xn là dãy các ĐLNN độc lập từng
đôi một, có kỳ vọng E(Xi) đều hữu hạn (
i 1,n
) và phƣơng sai
D(Xi) bị chặn trên bởi hằng số C (nghĩa là D(Xi) C, C là hằng số,
i 1,n
). Khi đó  > 0 ta có:
nn
ii
ni 1 i 1
11
limP X E(X ) 1
nn
 




.
Khi đó ta nói:
nn
(P)
ii
i 1 i 1
11
X E(X )
nn



.
Chứng minh:
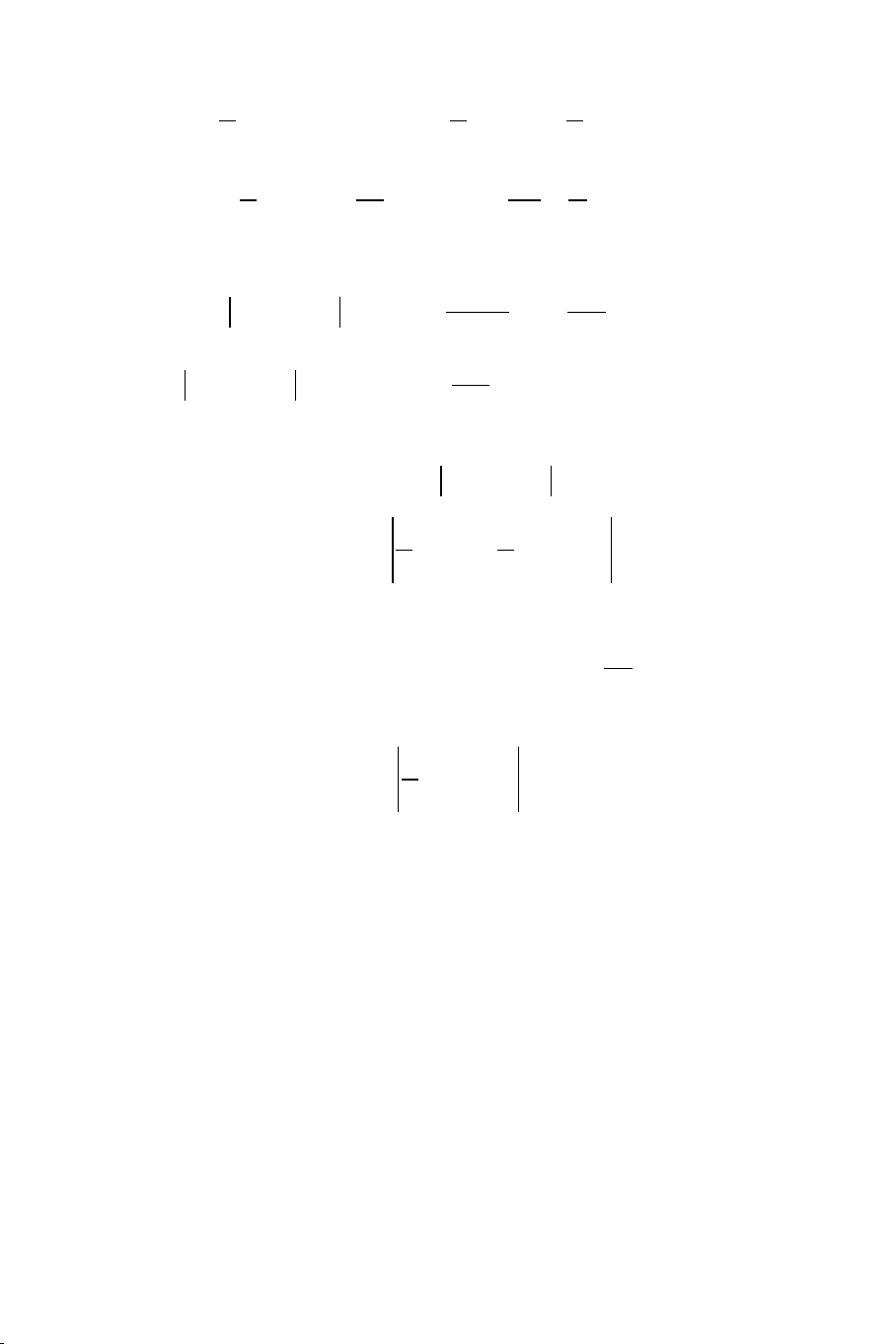
80
Đặt
n n n
n i n i i
i 1 i 1 i 1
1 1 1
S X E(S ) E X E(X )
n n n



và
nn
n i i
22
i 1 i 1
1 1 nC C
D(S ) D X D(X )
n n n n





.
Áp dụng bất đẳng thức Trê-bƣ-sép đối với ĐLNN Sn, ta có:
n
nn 22
D(S ) C
0,P S E(S ) 1 1 n

nn 2
nn
C
limP S E(S ) lim 1 1
n
 



Mà xác suất của một biến cố không vƣợt quá 1 nên:
nn
n
0,limP S E(S ) 1

nn
ii
ni 1 i 1
11
0,limP X E(X ) 1.
nn
 




฀
5.3.2. Hệ quả. Giả sử X1, X2, ..., Xn là dãy các ĐLNN độc lập
cùng tuân theo một quy luật phân phối xác suất nào đó với kỳ vọng
E(Xi) = và phƣơng sai D(Xi) = 2 hữu hạn (
i 1,n
). Khi đó  > 0
ta có:
n
i
ni1
1
limP X 1
n




Qua hệ quả trên ta thấy khi n khá lớn thì trung bình cộng các
ĐLNN có cùng kỳ vọng hầu nhƣ lấy những giá trị xấp xỉ kỳ vọng của
chúng và xấp xỉ này càng tốt nếu n càng lớn. Điều này có ý nghĩa thực
tiễn rất lớn, chẳng hạn nhƣ muốn đo đạc một đại lƣợng vật lý nào đó
ta cần thực hiện nhiều lần và lấy trung bình cộng của các kết quả làm
giá trị thực của đại lƣợng.
Nội dung hệ quả này còn là cơ sở cho một phƣơng pháp đƣợc áp
dụng trong thống kê là phƣơng pháp mẫu mà thực chất của nó là dựa
vào mẫu ngẫu nhiên để đi đến kết luận cho tổng thể các đối tƣợng
đƣợc nghiên cứu.
5.4. ĐỊNH LÝ BERNOULLI
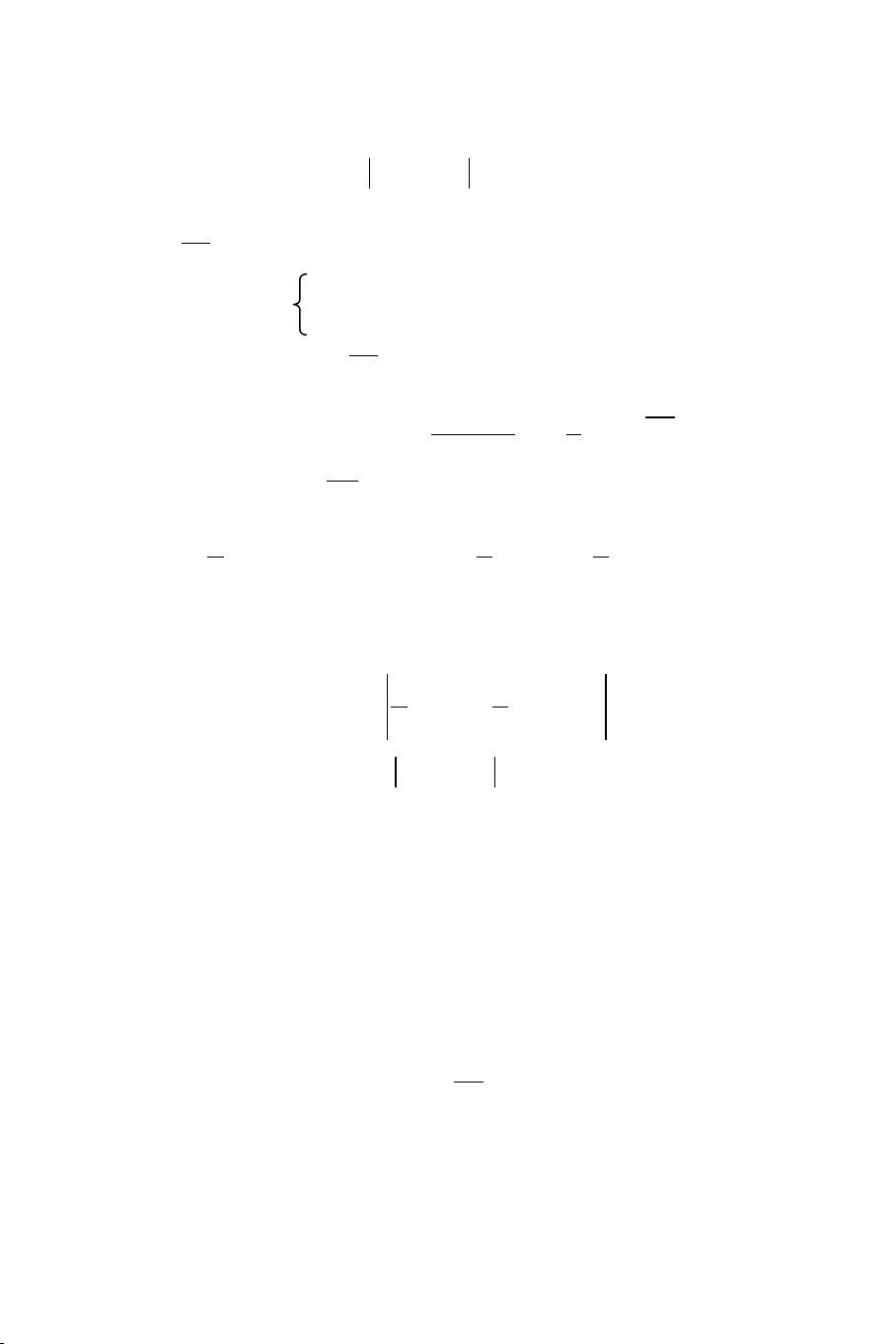
81
Định lý: Giả sử fn(A) là tần suất xuất hiện biến cố A trong n phép
thử độc lập và p là xác suất xuất hiện biến cố A trong mỗi phép thử.
Khi đó  > 0 ta có:
n
n
limP f (A) p 1

.
Chứng minh: Gọi Xi là số lần xuất hiện biến cố A trong phép thử
thứ i,
i 1,n
.
Ta có:
Do đó: Xi A(p) (
i 1,n
)
2
ii
p 1 p 1
E(X ) p;D(X ) p(1 p) , i 1,n.
24




D(Xi) bị chặn,
i 1,n
.
n n n
n i n i i
i 1 i 1 i 1
1 1 1
f (A) X E f (A) E X E(X ) p.
n n n



Áp dụng định lý Trê-bƣ-sép cho dãy các ĐLNN X1, X2, ..., Xn ở
trên ta có:
nn
ii
ni 1 i 1
11
0,limP X E(X ) 1
nn
 




n
n
limP f (A) p 1.

฀
Định lý Bernoulli nêu lên sự hội tụ theo xác suất của tần suất xuất
hiện biến cố trong n phép thử độc lập về xác suất xuất hiện biến cố đó
trong mỗi phép thử khi số phép thử tăng lên vô hạn. Do đó trong thực
tế khi số phép thử tăng lên khá lớn ta lấy fn(A) làm giá trị xấp xỉ cho
xác suất P(A).
5.5. ĐỊNH LÝ GIỚI HẠN TRUNG TÂM
Định lý. Giả sử X1, X2, ..., Xn là dãy các ĐLNN độc lập cùng tuân
theo một quy luật phân phối xác suất nào đó với kỳ vọng E(Xi) = và
phƣơng sai D(Xi) = 2 hữu hạn (
i 1,n
). Khi đó:
1 nếu A xuất hiện ở phép thử thứ i
0 nếu A không xuất hiện ở phép thử thứ i
i
X
82
Đại lƣợng ngẫu nhiên
1 2 n
X X ... X
Xn
sẽ hội tụ theo xác
suất tới một ĐLNN có quy luật phân phối xác suất chuẩn
2
N,
n



khi
n
.
hay đại lƣợng ngẫu nhiên
X
Un




sẽ hội tụ theo xác suất tới
quy luật phân phối xác suất chuẩn hóa N(0, 1) khi
n
.
Trong thực hành tính toán, khi n > 30 thì ta có thể xấp xỉ:
2X
X N , hay n N 0,1
n




 
.
Ví dụ. 1) Chọn ngẫu nhiên 192 số trên đoạn [0, 1]. Tìm xác suất để
tổng số điểm thu đƣợc X nằm trong khoảng (88, 104).
Giải. Ta có thể coi nhƣ
192
i
i1
XX
, trong đó mọi ĐLNN Xi độc
lập và cùng tuân theo quy luật phân phối đều U(0, 1).
Từ đó ta có E(Xi) =
01 0,5
2
; D(Xi) =
2
(1 0) 1
12 12
,
i 1,192
.
E(X) = 192.0,5 = 96 và D(X) = 192/12=16 = 4.
Vì vậy
P(88 X 104)
104 96 88 96 2 2 0,954.
44

2) Cho biến ngẫu nhiên X B(1000; 0,02). Tìm xác suất để X
nhận giá trị trong khoảng (40, 50).
Giải. Có thể coi
1000
i
i1
XX
, trong đó Xi độc lập và có cùng phân
phối không một A(0,02). Từ đó theo định lý giới hạn trung tâm suy ra
X N(, 2), trong đó = np = 1000.0,02 = 20; 2 = np(1 – p) = 19,6.
P(40 X 50)
50 20 40 20 6,77 4,51 0,5 4,999
19,6 19,6

= 0,001.