Chương 3
Tích phân và một số ứng dụng
Từ Chương 2, ta biết rằng nếu hàm số f(x)khả vi trong khoảng (a, b)thì có đạo
hàm trong khoảng (a, b)và ta hoàn toàn tính được đạo hàm của hàm số trong khoảng
đó. Một bài toán đặt ra là nếu cho trước một hàm số f(x)xác định trong khoảng (a, b)
thì liệu có tồn tại một hàm số F(x)khả vi trong khoảng (a, b)và F′(x) = f(x)với mọi
xthuộc khoảng (a, b), và nếu hàm F(x)như vậy tồn tại thì ta sẽ tìm hàm đó như thế
nào? Chương này nhằm trả lời câu hỏi đó. Bên cạnh đó, chúng ta sẽ tìm hiểu một số
ứng dụng quan trọng của bài toán trên trong nhiều lĩnh vực trong thực tế như kinh
tế, nông nghiệp và một số ngành khoa học khác.
3.1. Tích phân bất định
3.1.1. Nguyên hàm của hàm số
Định nghĩa 3.1.1. Nguyên hàm
Hàm F(x)được gọi là nguyên hàm của hàm f(x)nếu tại mọi điểm xthuộc miền
xác định của fta đều có F′(x) = f(x).
Nếu F(x)là một nguyên hàm của f(x)thì F(x) + C, với Clà hằng số cũng là một
nguyên hàm của f(x).
Ví dụ 3.1.2. Ta có các hàm số F(x) = x3;G(x) = x3+ 2; H(x) = x3+ 0,1đều
là các nguyên hàm của hàm số f(x) = 3x2vì đạo hàm của chúng đều bằng 3x2.
Định lí 3.1.3. Giả sử F(x)có đạo hàm trong (a, b)và F(x)là nguyên hàm của f(x)
với mọi x. Khi đó, ta có các khẳng định sau:
(1) Với mọi hằng số C, F (x) + Ccũng là một nguyên hàm của f(x),∀x∈(a, b).
(2) Ngược lại, mọi nguyên hàm của f(x),∀x∈(a, b)đều có dạng F(x) + C.
3.1.2. Tích phân bất định
Định nghĩa 3.1.4. Nếu f(x)có một nguyên hàm là F(x)thì nó có một họ các nguyên
hàm là F(x) + Cvới Clà một hằng số tùy ý và họ nguyên hàm đó được gọi là tích
phân bất định của hàm f(x).
56
Ký hiệu: Zf(x)dx, trong đó: Zlà dấu tích phân; xlà biến lấy tích phân; f(x)là
hàm dưới dấu tích phân; f(x)dx là biểu thức dưới dấu tích phân.
Như vậy theo định nghĩa Zf(x)dx =F(x) + C.
Ví dụ 3.1.5. Tính các tích phân sau: (a) Zx5dx;(b) Zsin xdx.
Giải: (a) Ta có Zx5dx =x6
6+Cvì x6
6+C!′
=x5.
(b) Zsin xdx =−cos x+Cvì (cos x)′= sin x.
•Các tính chất của tích phân bất định
(1) Zf(x)dx′=f(x); dZf(x)dx =f(x)dx;
(2) dF (x) = F(x) + Chay ZdF (x)
dx dx =ZF′(x)dx =ZdF (x) = F(x) + C;
(3) Zkf(x)dx =kZf(x)dx với klà một hằng số;
(4) Z(f(x) + g(x))dx =Zf(x)dx +Zg(x)dx;
(5) Nếu có Zf(x)dx =F(x) + Cvà u=ϕ(x)thì Zf(u)du =F(u) + C.
•Bảng các tích phân bất định của một số hàm cơ bản
1) Z0dx =C; 9) Zdx
1 + x2= arctan x+C;
2) Zxαdx =xα+1
α+ 1 +C(α6=−1);10) Zdx
√1−x2= arcsin x+C;
3) Z1
xdx = ln |x|+C; 11) Zdx
a2−x2=1
2aln
a+x
a−x
+C;
4) Zaxdx =ax
ln a+C; 12) Zf′(x)
pf(x)dx = 2pf(x) + C;
5) Zcos xdx = sin x+C; 13) Zdx
√x2+a= ln(x+√x2+a) + C;
6) Zsin xdx =−cos x+C; 14) Zdx
a2+x2=1
aarctan x
a+C;
7) Zdx
cos2x= tan x+C;15) Zdx
√a2−x2= arcsin x
a+C.
8) Zdx
sin2x=−cot x+C;
Chú ý 3.1.6. Từ định nghĩa nguyên hàm ta thấy phép tính đạo hàm và phép tính
nguyên hàm là hai phép tính ngược nhau nên từ bảng đạo hàm của một số hàm cơ bản
57
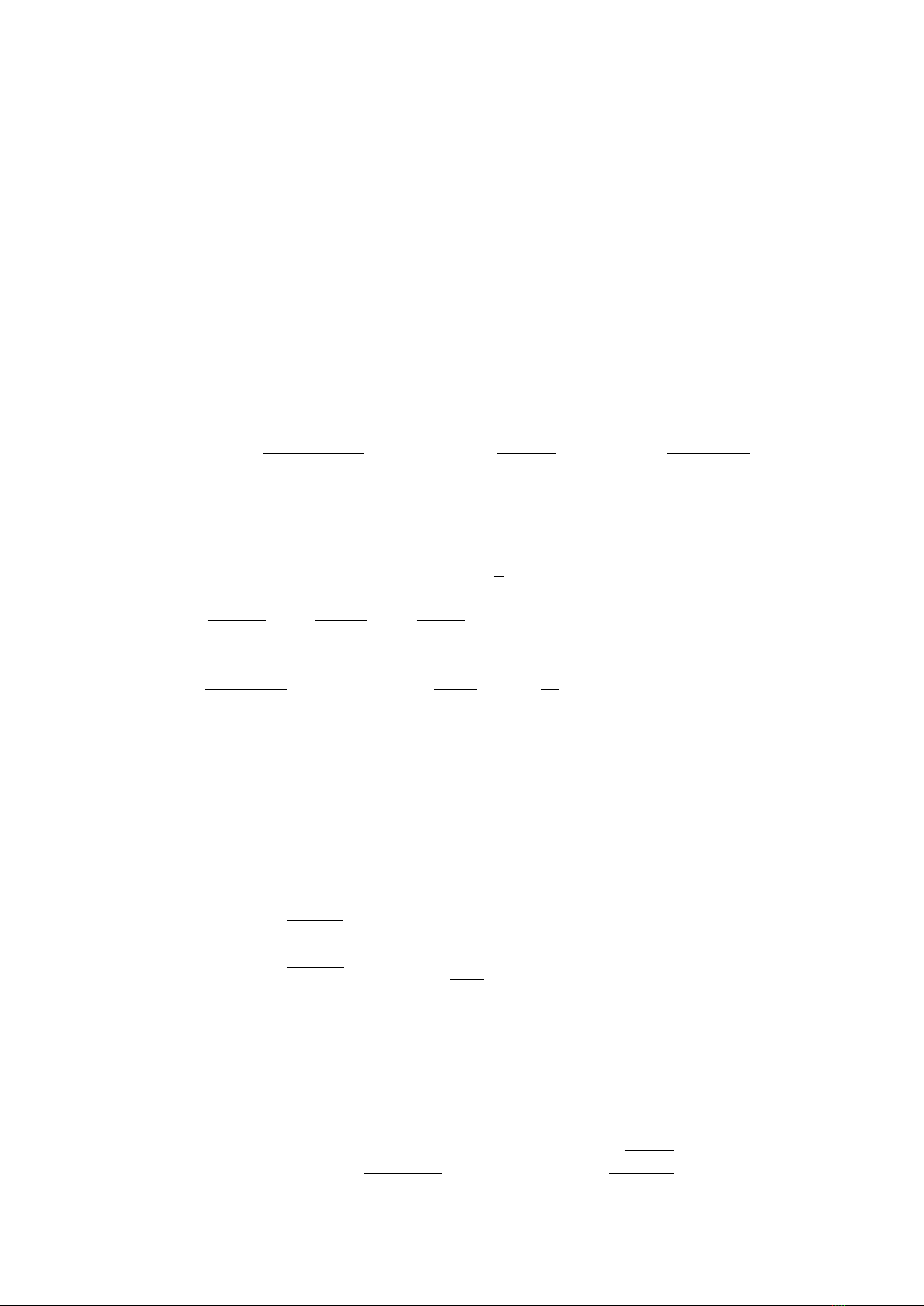
ta suy ra được bảng nguyên hàm của một số hàm cơ bản, chẳng hạn các tích phân từ
1 đến 10 trong bảng. Các tích phân từ 11 đến 15 ta có thể xây dựng dựa vào tính chất
của tích phân bất định và các tích phân đã biết.
3.1.3. Các phương pháp tính tích phân bất định
(a)Phương pháp tính trực tiếp
Sử dụng các tính chất và bảng tích phân bất định của một số hàm cơ bản để tính
trực tiếp một số tích phân đơn giản.
Ví dụ 3.1.7. Tính các tích phân
(a) Z3x2+ 2x−1
x2dx;(b) Zdx
1 + e−x;(c) Zx2+x+ 1
x−1dx.
Giải: (a) Z3x2+ 2x−1
x2dx =Z 3x2
x2+2x
x2−1
x2!dx =Z3 + 2
x−1
x2dx
= 3x+ 2 ln |x|+1
x+C.
(b) Zdx
1 + e−x=Zdx
1 + 1
ex
=Zexdx
ex+ 1 = ln(ex+ 1) + C.
(c) Zx2+x+ 1
x−1dx =Zx+ 2 + 3
x−1dx =x2
2+ 2x+ 3 ln |x−1|+C.
(b)Phương pháp đổi biến số
Cách 1: Giả sử cần tính tích phân Zf(x)dx. Đặt x=ϕ(t)với ϕ(t)là hàm đơn điệu,
ta có Zf(x)dx =Zf[ϕ(x)]ϕ′(x)dx, (3.1)
Trong một vài trường hợp việc tính tích phân mới này đơn giản hơn. Cách đặt này
thường áp dụng để đưa từ tích phân của hàm số vô tỷ mà có chứa các biểu thức sau:
(1) ZR(x, √a2+x2)dx, đặt x=atan t;
(2) ZR(x, √x2−a2)dx, đặt x=a
cos t;
(3) ZR(x, √a2−x2)dx, đặt x=asin t;
về tích phân của hàm lượng giác đơn giản hoặc từ tích phân của hàm hữu tỷ có chứa
biểu thức (x2+a2)về tích phân của hàm lượng giác.
Ví dụ 3.1.8. Tính các tích phân
(a)I=Zdx
(x2+a2)2; (b)I=Z√1−x2
x2dx.
58
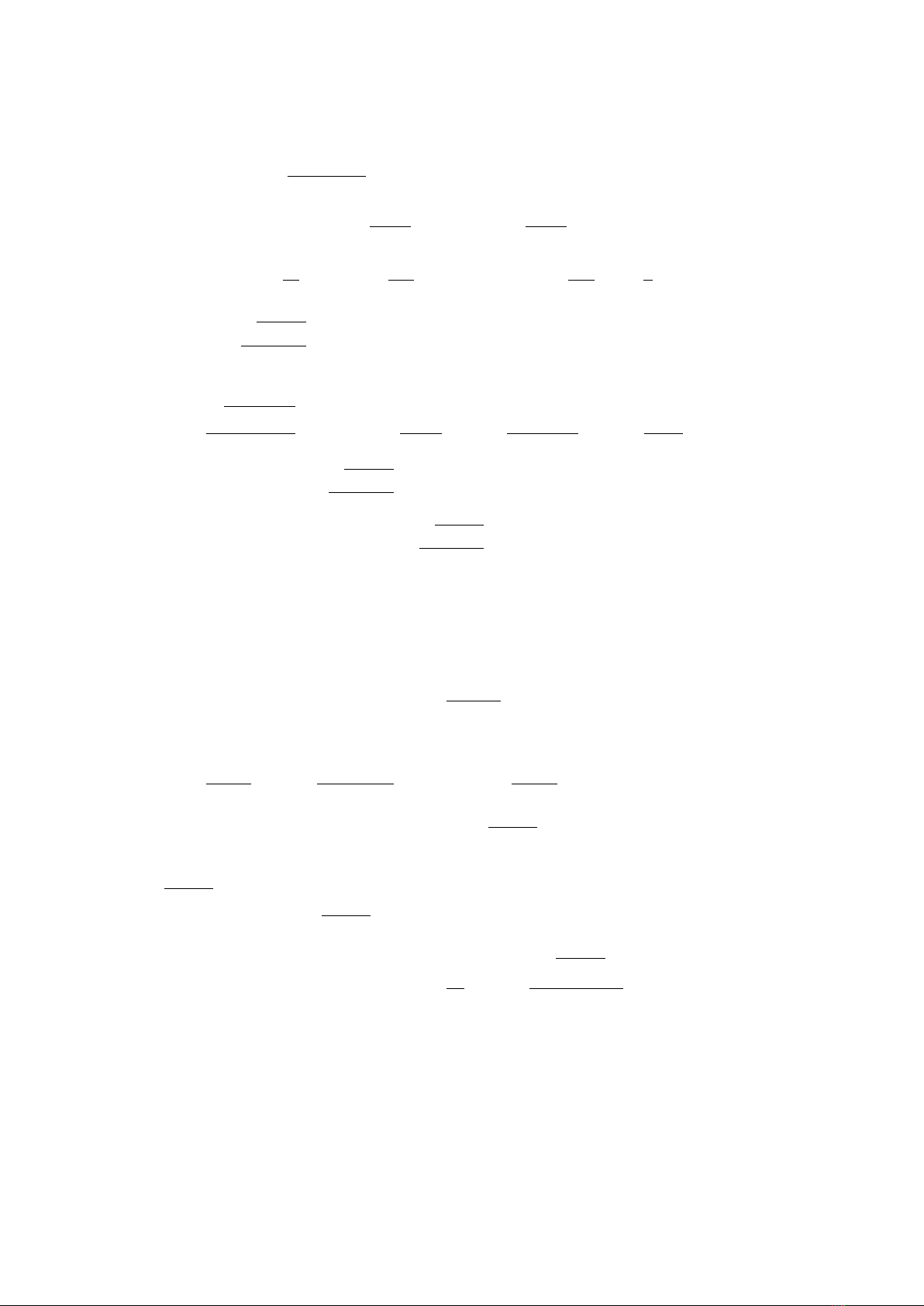
Giải: (a) I=Zdx
(x2+a2)2·
Đặt x=atan t⇒dx =adt
cos2t; (x2+a2)2=a4
cos4t·Vậy
I=Z1
a3cos2tdt =1
2a3Z(1 + cos 2t)dt =1
2a3t+1
2sin 2t+C.
(b) I=Z√1−x2
x2dx.
Đặt x= sin t⇒dx = cos tdt. Do đó:
I=Zp1−sin2t
sin2t·cos tdt =Zcos2t
sin2tdt =Z1−sin2t
sin2tdt =Zdt
sin2t−Zdt =−cot t−t+C.
Vì x= sin t⇒cot t=√1−x2
x;t= arcsin x. Vậy
I=−√1−x2
x−arcsin x+C.
Cách 2: Giả sử cần tính tích phân. Đặt t=ψ(x)với ψ(x)khả vi, tlà biến mới, khi
đó Zf[ψ(x)]ψ′(x)dx =Zf(t)dt. (3.2)
Ví dụ 3.1.9. Tính tích phân I=Ze3x
e2x+ 1dx.
Giải: Đặt t=ex⇒dt =exdx. Suy ra, ta có tích phân sau:
I=Zt2
t2+ 1dt =Zt2+ 1 −1
t2+ 1 dt =Zdt−Zdt
t2+ 1 =t−arctan t+C=ex−arctan ex+C.
Ví dụ 3.1.10. Tính tích phân I=Zx23
√1 + x3dx.
Giải: Ta nhận thấy x2dx đưa được về d(x3)nên để tính tích phân trên ta có thể đặt
3
√1 + x3=uhoặc cũng có thể đặt u= 1 + x3.
Chẳng hạn, đặt 3
√1 + x3=u⇒u3= 1 + x3⇒u2du =x2dx. Vậy
I=Zu.u2du =u4
4+C=3
√1 + x34
4+C.
Chú ý 3.1.11.
(1) Công thức (3.1) và (3.2) chứng minh bằng phương pháp lấy đạo hàm hai vế.
(2) Sau khi tìm được nguyên hàm ta phải trả lại vai trò cho biến cũ ban đầu.
(c)Phương pháp tích phân từng phần
Định lí 3.1.12. Giả sử u=u(x); v=v(x)là các hàm số có đạo hàm trên khoảng K,
ta có: Zudv =uv −Zvdu.
59
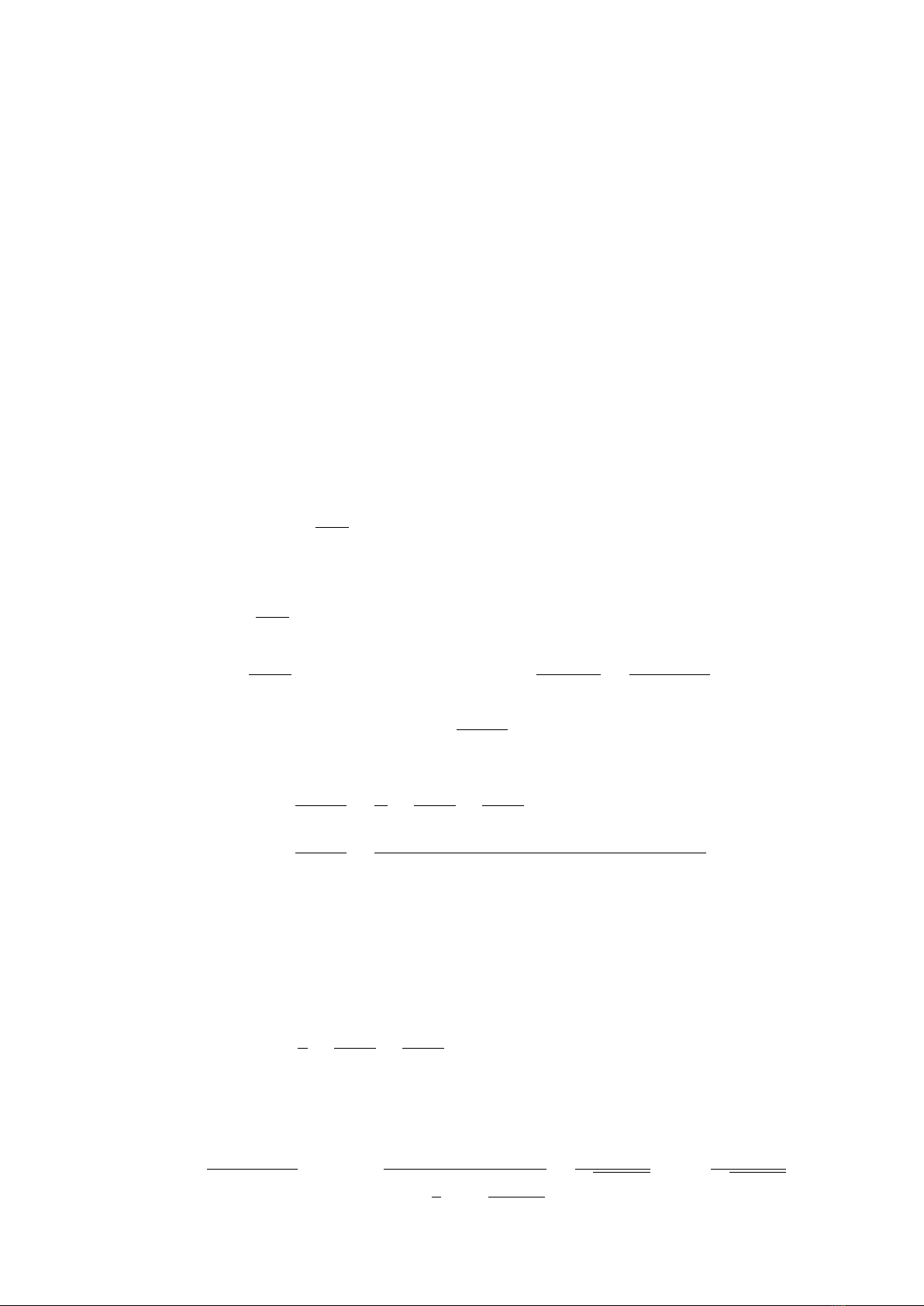
Chú ý 3.1.13. Công thức tích phân từng phần dùng để tính tích phân của một tích
các hàm số. Để tính được tích phân các hàm số này ta phải khéo léo lựa chọn hàm u
và dv.
Ví dụ 3.1.14. Tính tích phân I=Zx2exdx.
Giải: Đặt u=x2⇒du = 2xdx;dv =ex⇒v=ex⇒I=x2ex−2Zx.exdx.
Đặt u=x⇒du =dx;dv =ex⇒v=ex
⇒I=x2ex−2x.ex−Zexdx=x2ex−2xex+ 2ex+C.
3.1.4. Tích phân một số hàm cơ bản
(a)Tích phân các phân thức hữu tỷ
Xét tích phân Zp(x)
q(x)trong đó bậc của p(x)nhỏ hơn bậc của q(x).
•Nếu q(x)có nghiệm thực: Phân tích q(x)thành tích các nhị thức bậc nhất, tam
thức bậc hai sau đó dùng phương pháp hệ số bất định, hoặc phương pháp thêm bớt
để phân tích p(x)
q(x)thành tổng hoặc hiệu các phân thức có dạng:
Zdx
x±a= ln |x±a|+Choặc Zdx
(x±a)k=(x±a)1−k
1−k+C.
Ví dụ 3.1.15. Tính tích phân I=Zx−3
x3−xdx.
Giải: Ta có
x−3
x3−x=A
x+B
x−1+C
x+ 1
⇔x−3
x3−x=A(x−1)(x+ 1) + Bx(x+ 1) + Cx(x−1)
x3−x
⇒x−3 = A(x−1)(x+ 1) + Bx(x+ 1) + Cx(x−1) (3.3)
Vì (3.3) đúng với mọi giá trị của xnên đúng với giá trị xcụ thể.
Thay x= 0 :−3 = −A⇒A= 3.
Thay x= 1 :−2 = 2B⇒B=−1.
Thay x=−1:−4 = 2C⇒C=−2.
Vậy I=Z3
x−1
x−1−2
x+ 1dx= 3 ln |x| − ln |x−1| − 2 ln |x+ 1|+C.
•Nếu q(x) = x2+px +qtrong đó p2−4q <0
+ Xét q(x) = A
I=ZA
x2+px +qdx =AZdx
x+p
22
+4q−p2
4
=2A
p4q−p2arctan 2x+p
p4q−p2+C.
60