- 93 -
CHƯƠNG 5. HÀM SỐ NHIỀU BIẾN SỐ
5.1 Các khái niệm cơ bản
5.1.1. Hàm số hai biến số
5.1.1.1. Khái niệm hàm số hai biến số.
Khái niệm hàm số một biến số phản ánh sự phụ thuộc hàm số của một
biến số vào một biến số khác: mỗi giá trị của biến độc lập được đặt tương ứng
với một giá trị của biến phụ thuộc. Trong thực tế, nhiều khi một biến số phụ
thuộc không chỉ vào một mà còn phụ thuộc đồng thời vào nhiều biến số khác. Ví
dụ: sản lượng, tức là số lượng sản phẩm của một nhà sản xuất, phụ thuộc vào
mức sử dụng các yếu tố đầu vào như lao động, vốn, …
Khái niệm hàm số n biến số phản ánh sự phụ thuộc hàm số của một biến
số vào n biến số khác. Để đơn giản trước hết ta đề cập đến trường hợp n = 2.
Cho một cặp biến số có thứ tự (x; y), ta có thể đồng nhất mỗi cặp số với
một điểm M(x; y) của mặt phẳng. Mặt phẳng tọa độ được gọi là không gian hai
chiều và ký hiệu là
2
. Theo quan điểm này, một cặp biến số (x; y) được xem
như một biến điểm M(x; y) với miền biến thiên là một tập hợp D của không gian
2
.
Định nghĩa 1. Một hàm số f của biến điểm M(x; y), với miền biến thiên
2
D
,
là quy tắc đặt tương ứng mỗi điểm M(x; y) D với một và chỉ một số thực z.
Miền D được gọi là miền xác định của hàm số f, số thực z ứng với điểm
M(x; y) được gọi là giá trị của hàm f tại M(x; y) và được ký hiệu là f(M) hoặc
f(x; y). Hàm f được xác định như trên được gọi là hàm số hai biến số x và y. x, y
được gọi là các biến số độc lập; z là biến số phụ thuộc hàm số vào các biến x, y.
Khi cho một hàm hai biến, các cách diễn đạt sau là như nhau:
- Hàm số f xác định trên miền
2
D
;
- Hàm số f(M), M D;
- Hàm số f(x; y), (x; y) D;
- Hàm số z = f(x; y), (x; y) D.
5.1.1.2. Miền xác định của hàm số
- 94 -
Miền xác định của hàm hai biến z = f(x; y) là miền biến thiên của biến
điểm M. Nếu biểu diễn hình học thì miền biến thiên là một tập hợp trong mặt
phẳng tọa độ.
Thông thường một hàm của hai biến x, y được cho dưới dạng một biểu
thức f(x; y). Mỗi biểu thức có một miền xác định tự nhiên của nó. Miền xác định
tự nhiên của một biểu thức tập hợp tất cả các cặp số thực (x; y) mà biểu thức đó
có nghĩa khi ta gán các giá trị x, y. Nói chung miền xác định của một hàm hai
biến cho dưới dạng biểu thức có thể là tập con D bất kỳ của miền xác định tự
nhiên của biểu thức đó. Ta quy ước, nếu không nói gì thêm về miền xác định
của một biểu thức thì miền xác định của nó được hiểu là miền xác định tự nhiên.
Ví dụ 5.1: Miền xác định của hàm số z = x + y là toàn bộ mặt phẳng x0y.
Ví dụ 5.2: Miền xác định của hàm số
2 2
ln 4 z x y
là tập tất cả các điểm
M(x; y) thỏa mãn điều kiện x2 + y2 < 4. Như vậy miền xác định là hình tròn có
tâm ở gốc tọa độ có bán kính r = 2, không kể các điểm trên đường tròn.
5.1.1.3. Đồ thị hàm hai biến.
Để biểu diễn hình học quan hệ hàm số z = f(x; y) trong không gian ba
chiều, ta dùng hệ tọa độ vuông góc với trục hoành 0x biểu diễn biến số x, trục
tung 0y biểu diễn biến số y và trục cao 0z biểu diễn biến phụ thuộc z.
Miền xác định D của hàm số z = f(x; y) là một tập hợp điểm trên mặt
phẳng (0xy). Mỗi điểm M(x; y) cho tương ứng một giá trị của hàm số z, theo đó
ta có tương ứng một điểm P(x; y; z) trong không gian.
Định nghĩa 2. Đồ thị của hàm số z = f(x; y) là tập hợp tất cả các điểm P(x; y; z)
trong không gian, trong đó M(x; y) là điểm bất kỳ thuộc miền xác định D và z là
giá trị của hàm số tại điểm đó.
Ví dụ 5.3: Đồ thị hàm số z =
2 2
4
x y
là nửa mặt cầu có tâm ở gốc tọa độ và
bán kính R = 2.
5.1.1.4. Đường mức
Cho z = f(x; y) là hàm số xác định trong miền D và z0 là một giá trị cố
định của hàm số đó.
Định nghĩa 3. Đường mức của hàm số z = f(x; y) là tập hợp tất cả các điểm
M(x ; y) thỏa mãn điều kiện : f(x; y) = z0 , với z0 là một giá trị cố định. Nói cách
khác, đường mức của hàm hai biến z = f(x; y) là tập hợp tất cả các điểm của mặt
phẳng ( 0xy ) mà tại đó hàm số nhận cùng một giá trị z0 cố định.
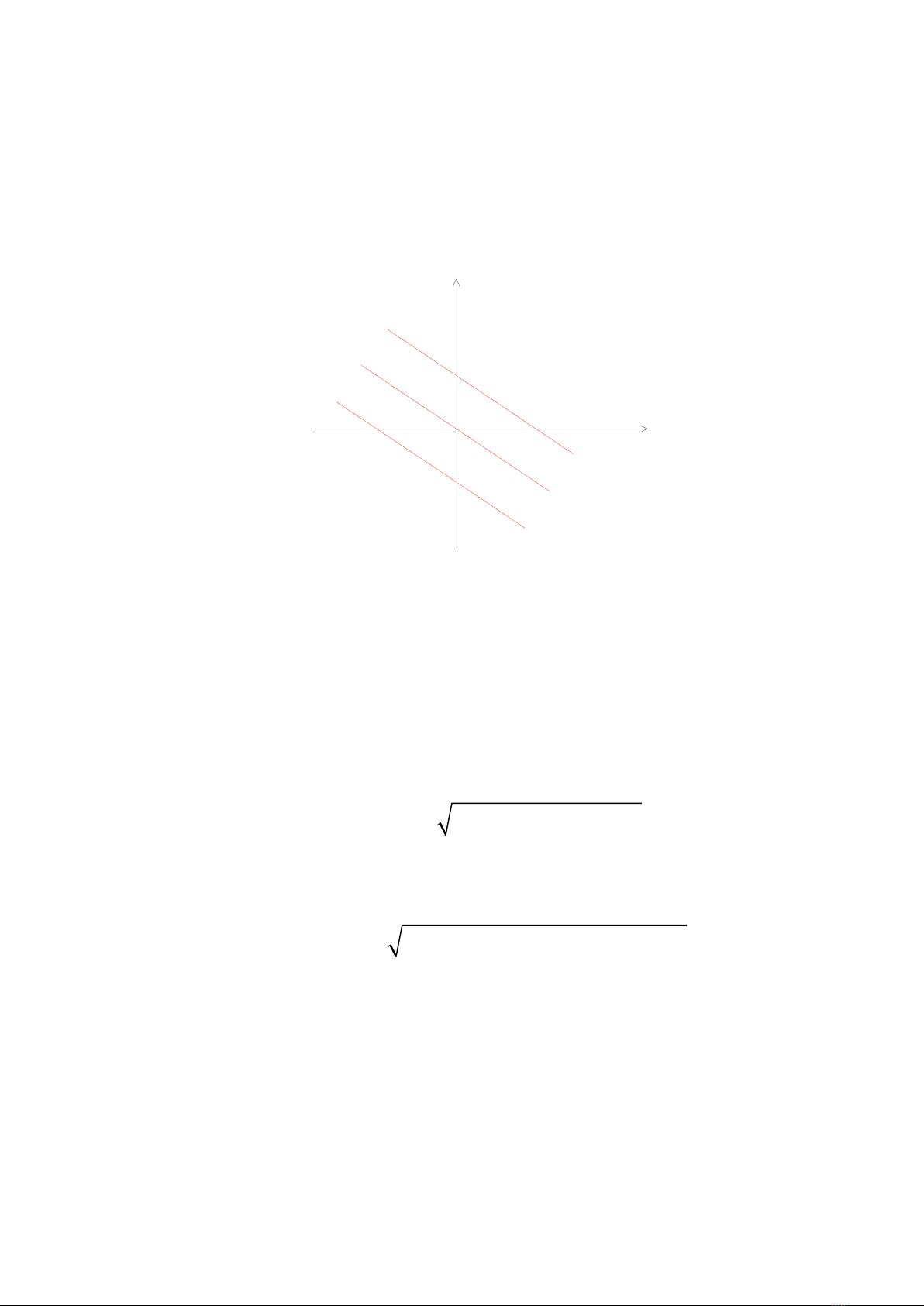
- 95 -
Thông thường đường mức của một hàm hai biến là một đường trên mặt
phẳng. Mỗi giá trị z0 cố định tương ứng với một đường mức.
Ví dụ 5.4: Các đường mức của hàm số
2 3z x y
là các đường thẳng có
phương trình
0
2 3
x y z
, với z0 là hằng số. trên hình 5.1 là các đường mức của
hàm số này ứng với các giá trị 0 0 0
6; 0; 6
z z z
2x + 3y = -6
2x + 3y = 0
2x + 3y = 6
-3
-2
2
3
x
Oy
5.1.2. Hàm số n biến số
5.1.2.1. Không gian điểm n chiều
Theo phương pháp tọa độ, mỗi điểm trên mặt phẳng được đồng nhất với
một bộ hai số thực có thứ tự (x; y) và mỗi điểm trong không gian ba chiều được
đồng nhất với bộ ba số có thứ tự (x; y; z).
Trên mặt phẳng tọa độ (trong không gian hai chiều) khoảng cách giữa hai
điểm M(x; y) và M’(x’; y’) được xác định theo công thức:
2 2
( ; ') ( ') ( ') .d M M x x y y
Tương tự, trong không gian ba chiều khoảng cách giữa hai điểm M(x; y;
z) và M’(x’; y’; z’) được xác định theo công thức:
Một cách tổng quát ta có định nghĩa điểm n chiều và không gian n chiều
như sau:
Định nghĩa 4. Mỗi bộ n số thực có thứ tự 1 2
( ; ; ; )
n
x x x
được gọi là một điểm
n chiều.
Để gán tên cho điểm n chiều 1 2
( ; ; ; )
n
x x x
ta dùng các chữ cái in hoa,
chẳng hạn điểm X thì ta viết:
1 2
( ; ; ; )
n
X x x x
hoặc 1 2
( ; ; ; )
n
X x x x
- 96 -
Định nghĩa 5. Không gian điểm n chiều (gọi tắt là không gian n chiều) là tập
hợp tất cả các điểm n chiều, trong đó khoảng cách giữa hai điểm
1 2
( ; ; ; )
n
X x x x
và 1 2
'( ' ; ' ; ; ' )
n
X x x x
được xác định theo công thức:
' 2 ' 2 ' 2
1 1 2 2
( ; ') ( ) ( ) ... ( ) .
n n
d X X x x x x x x (5.1.1)
Không gian n chiều được ký hiệu là
n
Ta có thể chứng minh được rằng khoảng cách trong không gian
n
, xác
định theo công thức (5.1.1), thỏa mãn các tính chất đã biết của khoảng cách
trong không gian hai chiều và không gian ba chiều:
Với bất kỳ ba điểm X, X’, X” thuộc không gian
n
ta có:
(i) d(X; X’) 0, d(X; X’) = 0 X = X’(xi = xi’ với mọi i = 1, 2,…, n).
(ii) d(X ; X’) = d(X’ ; X).
(iii) d(X; X’) + d(X’; X’’)
d(X; X’’).
5.1.2.2. Khái niệm hàm số n biến số
Định nghĩa 6. Một hàm số f của biến điểm 1 2
( ; ; ; )
n
X x x x
, với miền biến
thiên D
n
, là quy tắc đặt tương ứng mỗi điểm 1 2
( ; ; ; )
n
X x x x
D với
một và chỉ một số thực z.
Miền D được gọi là miền xác định của hàm số f, số thực z ứng với điểm
1 2
( ; ; ; )
n
X x x x
được gọi là giá trị của hàm f tại X và được ký hiệu là f(X)
hoặc f(x1; x2; …; xn). Hàm f được định nghĩa như trên được gọi là hàm số n biến
số.
Các khái niệm khác của hàm số n biến số được định nghĩa tương tự như
đã định nghĩa ở hàm hai biến số.
5.1.3. Các hàm số thường gặp trong phân tích kinh tế
Để tiếp cận với các phương pháp phân tích định lượng trong kinh tế học,
ta hãy làm quen với một số hàm số mà các nhà kinh tế hay sử dụng khi phân tích
các hoạt động kinh tế. Các ký hiệu biến số kinh tế đưa ra ở đây là các ký hiệu
thông dụng trong các tài liệu về kinh tế học, thường là lấy các chữ cái đầu của từ
tiếng Anh tương ứng.
5.1.3.1. Hàm sản xuất.
- 97 -
Hàm sản xuất là hàm số biểu diễn sự phụ thuộc của sản lượng tiềm năng
của một doanh nghiệp vào lượng sử dụng các yếu tố sản xuất. Khi phân tích hoạt
động sản xuất, các nhà kinh tế thường lưu tâm đến hai yếu tố sản xuất quan
trọng nhất là tư bản (capital và lao động (labor). Gọi K là lượng tư bản (vốn) và
L là lượng lao động được sử dụng. Với trình độ công nghệ của mình, khi sử
dụng K đơn vị tư bản và L đơn vị lao động, doanh nghiệp có khả năng sản xuất
một lượng sản phẩm tối đa, ký hiệu là Q (gọi là sản lượng tiềm năng). Hàm sản
xuất có dạng:
; Q f K L
(5.1.2)
Hàm số (5.1.2) cho biết số lượng sản phẩm mà doanh nghiệp có khả năng
sản xuất được ở mỗi mức sử dụng kết hợp vốn và lao động. Khi phân tích sản
xuất, người ta giả thiết rằng các doanh nghiệp khai thác hết khả năng công nghệ,
tức là Q luôn luôn là sản lượng tiềm năng, do đó hàm sản xuất f là do công nghệ
xác định.
Dạng hàm sản xuất mà các nhà kinh tế học hay sử dụng là hàm Cobb –
Douglas:
Q ,aK L
trong đó
, ,a
là các hằng số dương.
Đường mức của hàm sản xuất có phương trình:
0 0 0
( ; ) ( , 0)
f K L Q Q const Q
Trong kinh tế học, thuật ngữ “ đường mức ” của hàm sản xuất có tên gọi
là đường đồng lượng, hay đường đẳng lượng (isoquant). Đường đồng lượng là
tập hợp các yếu tố sản xuất (K; L) cho cùng một mức sản lượng Q0 cố định.
5.1.3.2. Hàm chi phí và hàm lợi nhuận.
Như ta đã biết, tổng chi phí sản xuất TC (Total cost) tính theo sản lượng
gọi là hàm chi phí, có dạng:
( )TC TC Q
Nếu tính theo các yếu tố sản xuất thì hàm chi phí là hàm số của các yếu tố
sản xuất:
0
K L
TC w K w L C