Giáo trình Vật lý 2 ThS. Trương Thành
101
CHƯƠNG X
CƠ LƯỢNG TỬ
Mục đích của chương này là khảo sát những tính chất và quy luật vận
động của các hạt trong phạm vi kích thước của phân tử, nguyên tử.
10.1. TÍNH SÓNG HẠT CỦA VẬT
CHẤT TRONG THẾ GIỚI VI MÔ
10.1.1. TÍNH SÓNG HẠT CỦA ÁNH SÁNG
Trong phần quang học chúng ta đã nghiên cứu các hiện tượng chứng tỏ
ánh sáng có bản chất sóng điện từ như hiện tượng giao thoa, nhiễu xạ, phản
cực v.v... Việc giải thích các hiện tượng này dựa trên cơ sở xem ánh có bản
chất sóng. Chẳng hạn, sự truyền một chùm ánh sáng song song đơn sắc có thể
coi là sự truyền những sóng phẳng đơn sắc, mặt sóng vuông với tia sóng .
Giả sử biểu thức của dao động sóng ở O là:
x = acos2πνt.
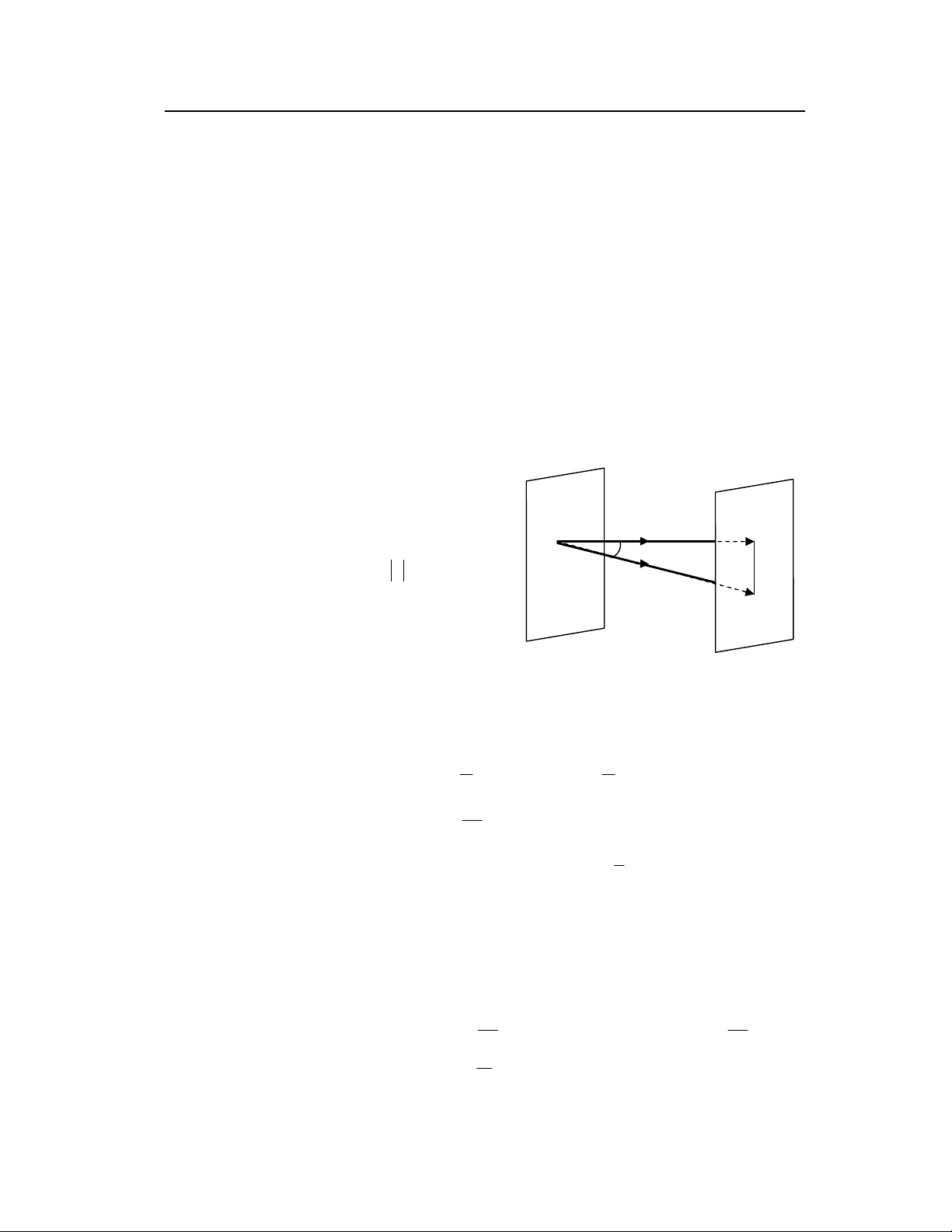
Trong đó ν là tần số dao động sóng. Ta
hãy tìm biểu thức của dao động sóng tại
điểm M bất kỳ ( rMO
r
r
=). Mặt sóng đi
qua M cách mặt sóng đi qua O một đoạn
d: d = rcos α = r n
r
cosα
Trong đó n
r là vector pháp tuyến đơn vị
nằm theo phương truyền của sóng ánh
sáng, α là góc hợp bởi n
r và
r
r
. Như vậy
ta có thể viết : nrd rr.=
Biểu thức của dao động sáng trên
mặt sóng đi qua M (nghĩa là biểu thức của dao động sáng tại điểm M) có
dạng:
x = acos 2πν(c
d
t−) = acos2π(
λ
d
vt −)
x = acos 2π (
λ
nr
vt
r
r
−) (X-1).
Trong đó c là vận tốc ánh sáng trong chân không, λ = v
c là bước sóng của ánh
sáng trong chân không.
Trong cơ học lượng tử để thuận lợi cho việc tính toán người ta viết hàm
sóng dưới dạng số phức (dựa vào công thức Euler)
α
i
e− = cosα - isinα.
Nghĩa là hàm sóng thực là phần thực của hàm phức:
ψ
= 0
ψ
cos 2π (
λ
nr
vt
r
r
−) + 0
ψ
isin 2π (
λ
nr
vt
r
r
−)
)
.
(2
0
λ
π
ψ
ψ
nr
vti
e
r
r
−−
= (X-2).
n
r
d
r
r
α
α
M’
M
O
Hình X-1

Giáo trình Vật lý 2 ThS. Trương Thành
102
Chú ý rằng do tiện ích của số phức mà ta dùng hàm sóng
ψ
nhưng hàm sóng
thực chính là phần thực (x) của số phức này, nghĩa là trong
ψ
còn có sóng ảo.
Đối với những hiện tượng khác như: hiện tượng quang điện, Compton,
áp suất ánh sáng v.v..., ánh sáng biểu hiện rõ tính chất hạt. Việc giải thích các
hiện tượng này phải dựa trên cơ sở xem ánh sáng cấu tạo bởi những hạt
photon, mỗi hạt mang năng lượng E = hν và chuyển động với vận tốc bằng c.
Theo thuyết tương đối, năng lượng E của photon bằng: E = 2
mc
Do đó, khối lượng m của photon: m = 2
c
hv ,
và động lượng của nó : p = mc = c
E =
λ
h
Như vậy: ánh sáng vừa có tính sóng, vừa có tính hạt. Ta nói rằng ánh
sáng có lưỡng tính sóng hạt. Trong một số hiện tượng thì ánh sáng biểu hiện
rõ rệt tính chất sóng, ngược lại trong một số hiện tượng khác tính chất hạt thể
hiện rõ rệt hơn. Những đại lượng đặc trưng cho tính chất hạt của ánh sáng (E,
p
r
) và cho tính chất sóng (ν, λ) liên hệ với nhau bởi các công thức trên.
Mặt khác do: h
P
=
λ
π
2, h
E
=
πν
2 nên trên ta có thể viết hàm sóng ánh
sáng dưới dạng: )..( rpEt
i
aex
rr
h−
−
=
với:
π
2
h
=
h = 1,05 . 34
10− Js.
10.1.2. GIẢ THUYẾT DE BRÖGLIE
Trên cơ sở lưỡng tính sóng hạt của ánh sáng De Bröglie đã mở rộng tính
chất đó đối với điện tử và sau đó đối với mọi vật thể với hai nội dung sau:
Mỗi hạt vi mô chuyển động tự do có năng lượng E và động lượng P xác
định được gắn liền với một sóng phẳng đơn sắc có:
- Năng lượng: E = hν (X-3).
- Động lượng p:
λ
h
p= (X-4).
10.1.3. THỰC NGHIỆM XÁC NHẬN LƯỠNG TÍNH SÓNG HẠT CỦA
HẠT VI MÔ
Giả thuyết De Bröglie về lưỡng tính sóng hạt của mọi vi hạt đã được
nhiều sự kiện thực nghiệm xác nhận. Ở đây chúng ta sẽ xét hai thí nghiệm cơ
bản:
10.1.3.1. Thí nghiệm 1
Ta cho một chùm điện tử đi qua một khe hẹp. Hứng chùm điện tử trên
màn huỳnh quang và dùng kính quan sát hay chụp ảnh, ta sẽ thu được các vân
nhiễu xạ giống như các vân nhiễu xạ của ánh sáng qua một khe. Nếu cho từng
điện tử riêng biệt đi qua khe thì trên màn huỳnh quang ta sẽ thu được những
ảnh rời rạc của điện tử. Tuy nhiên nếu thời gian thí nghiệm khá lâu, để số điện

Giáo trình Vật lý 2 ThS. Trương Thành
103
tử qua khe đủ lớn, thì mặc dù cho từng điện tử riêng biệt đi qua khe, ta vẫn
thu được các vân nhiễu xạ trên màn huỳnh quang. Như vậy khi qua khe hẹp
điện tử bị nhiễu xạ, tức là điện tử có tính chất sóng.
10.1.3.2. Thí nghiệm 2 (Davisson – Germer).
Ta hãy cho một chùm điện tử đập thẳng góc vào mặt tinh thể Ni. Chùm
điện tử sẽ tán xạ trên mặt tinh thể dưới những góc khác nhau. Hiện tượng tán
xạ này xảy ra giống như hiện tượng nhiễu xạ của tia X trên mặt tinh thể Ni.
Việc xác định vị trí các vân nhiễu xạ cho phép ta tìm được bước sóng λ của
điện tử theo công thức thông thường tính các cực đại nhiễu xạ của một nhiều
khe: d sin ϕ = kλ
Trong đó d là khoảng cách giữa hai lớp ion liên tiếp của tinh thể, ϕ là góc tán
xạ của hạt. Kết quả này phù hợp với phép tính λ theo công thức.
Ngoài ra người ta còn làm được nhiều thí nghiệm về giao thoa; nhiễu
xạ của các hạt vi mô khác.
Tất cả các kết quả thực nghiệm đều xác nhận tính chất sóng của mọi hạt
vi mô và do đó chứng minh sự đúng đắn của giả thuyết De Bröglie .
10.1.4. Ý NGHĨA THỐNG KÊ CỦA HÀM SÓNG
Theo giả thuyết De BrÖglie, chuyển động của các hạt tự do (hạt không
chịu tác dụng của ngoại lực) được mô tả bởi hàm sóng tương tự như sóng
phẳng ánh sáng đơn sắc:
).( rpEt
h
i
oe
rr
−−
=
ψ
ψ
(X-5).
Biên độ của hàm số sóng o
ψ
được cho bởi:
*
2
ψψ
ψ
=
ψ* là liên hợp phức của ψ, ( ).(
0
*rpEt
h
i
e
rr
−
=
ψ
ψ
) (X-6).
Biểu thức (X-5) là hàm số sóng của các hạt tự do. Còn nói chung đối
với các hạt vi mô chuyển động trong trường thế, hàm số sóng của nó là một
hàm phức tạp của
r
r
và t.
ψ
ψ
ψ
=
=
),( tr
r
(x,y,z,t)
Dưới đây, ta sẽ xét ý nghĩa của hàm số
sóng nói trên. Để cụ thể ta xét một chùm hạt
photon truyền trong không gian và giả sử dV là
một phần tử thể tích vô cùng nhor bất kỳ trong
không gian bao quanh điểm M có hàm sóng ψ.
Theo quan điểm sóng cường độ sáng tại M tỉ lệ
với bình phương biên độ dao động sóng 2
o
ψ
tại M: 2
o
ψ
càng lớn thì điểm M
càng sáng.
Theo quan điểm hạt, cường độ sáng tại M tỉ lệ với năng lượng của các
hạt trong đơn vị thể tích bao quanh M, nghĩa là tỉ lệ với số hạt trong đơn vị
thể tích. Do đó, số hạt trong đơn vị thể tích bao quanh M tỉ lệ với bình
Hình X-2
M
dV c

Giáo trình Vật lý 2 ThS. Trương Thành
104
phương biên độ sóng ánh sáng tại đó. Nghĩa là số hạt trong đơn vị thể tích tỷ
lệ với 2
2
ψ
ψ
=
o. Nếu số hạt trong đơn vị thể tích càng nhiều thì khả năng tìm
thấy hạt trong đó càng lớn. Vì thế có thể nói, bình phương biên độ sóng
ψ
2
tại M đặc trưng cho khả năng tìm thấy hạt trong đơn vị thể tích bao quanh M.
Ta gọi
ψ
2 là mật độ xác suất (xác suất tìm thấy hạt trong một đơn vị thể tích).
2
ψω
=.
Như vậy xác suất tìm thấy hạt trong thể tích bất kỳ dV sẽ bằng:
dVd 2
W
ψ
=,
và xác suất tìm thấy hạt trong không gian V nào đó bằng:
∫∫∫
=
V
dV
2
W
ψ
.
Nếu tìm hạt trong toàn không gian chứa hạt thì chắc chắn sẽ tìm thấy
hạt, nghĩa là xác suất tìm hạt trong toàn không gian đó phải bằng 1:
∫∫∫ =1
2dV
ψ
Điều kiện trên gọi là điều kiện chuẩn hoá hàm sóng.
Tóm lại, ta có thể đưa ra một số kết luận sau:
- Trạng thái của một hạt vi mô tại vị trí x, y, z và ở thời điểm t được xác
định bởi hàm số sóng
ψ
(x, y, z, t).
-
ψ
2 biểu diễn mật độ xác suất tìm thấy hạt tại vị trí và thời điểm đó.
Như vậy hàm số sóng ψ không mô tả một sóng thực nào trong không
gian như sóng cơ, sóng điện từ trong vật lý cổ điển, mà chỉ cho phép ta tính
xác suất tìm hạt tại một vị trí và thời điểm nào đó.
Do yêu cầu của các điều kiện vật lý và toán học hàm số này phải liên
tục, đơn trị, hữu hạn và đạo hàm bậc nhất của nó cũng phải liên tục.
Giáo trình Vật lý 2 ThS. Trương Thành
105
10.2. HỆ THỨC BẤT ĐỊNH HEISENBERG
10.2.1. HỆ THỨC
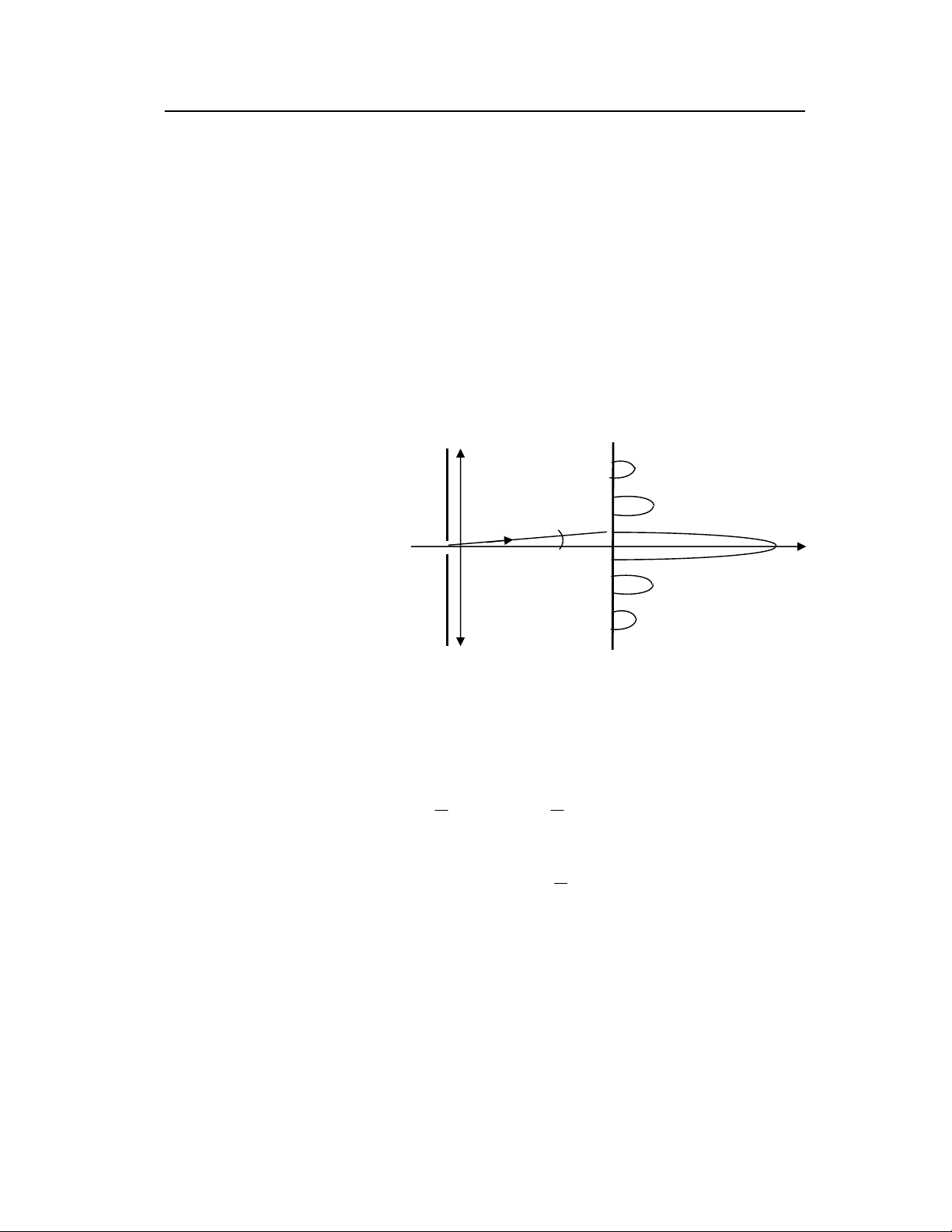
Để đi đến hệ thức bất định ta lại xét hiện tượng nhiễu xạ của một chùm
hạt (photon, điện tử...) qua một khe có bề rộng b. Sau khi qua khe, hạt bị
nhiễu xạ theo những phương khác nhau. Tuỳ theo trị số của góc nhiễu xạ ϕ,
mật độ chùm hạt nhiễu xạ trên màn sẽ cực đại hoặc cực tiểu (bằng không).
Ta hãy xét vị trí của hạt trong khe. Để đơn giản, ta xét toạ độ của hạt
theo một phương x nằm trong mặt phẳng của khe và song song với chiều rộng
của khe. Toạ độ x của hạt trong khe có những giá trị ở trong khoảng từ 0 đến
b (b là bề rộng của khe).
0 ≤ x ≤ b
Như vậy nếu tìm hạt trong khe thì tọa độ của hạt có độ bất định lớn nhất là:
∆x ≈ b
Mặt khác sau khi qua
khe, phương động hướng p
r
của hạt thay đổi. Hình chiếu
p
r
theo phương x sẽ có giá
trị thay đổi trong khoảng
0 ≤ Px ≤ psin ϕ
Nghĩa là sau khi qua khe,
các hạt có thể rơi vào cực
đại chính hoặc các cực đại
phụ. Cho nên x
p được xác
định với độ bất định nào đó.
Hình chiếu x
p được xác định với độ bất định nhỏ nhất x
p
∆
tương ứng với hạt
rơi vào cực đại chính là: 1
sin
ϕ
ppx
≈
∆
ϕ1 là góc ứng với cực tiểu thứ nhất:
b
λ
ϕ
=
1
sin b
ppx
λ
≈∆⇒
Như vậy:
λ
ppx x
=
∆
∆.
Nhưng theo Theo giả thuyết De Bröglie thì
λ
h
p=, do đó ta có:
hpx x
≈
∆
∆. (X-7).
Đó là hệ thức bất định Heisenberg
10.2.2. VÍ DỤ
Trong nguyên tử, điện tử chuyển động trong phạm vi 10-8 cm (cở kích
thước nguyên tử). Hãy tìm độ chính xác của vận tốc khi ta xác định nó.
Theo bài ra thì độ bất định lớn nhất về vị trí của điện tử là: mx 10
10−
≈∆ ,
do đó độ bất định về vận tốc bằng:
p
r
ϕ1
Hình X-3
b











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














