Phùng Danh Thắng Đại học TM
GợI ý BàI TậP KINH Tế VI MÔ
Bài tập 1
Vẽ đường giới hạn khả năng sản xuất, lấy trục hoành là số lượng lương
thực, trục tung là số lượng quần áo. Chi phí cơ hội để sản xuất thêm
một đơn vị lương thực là số lượng quần áo phải mất đi.
Vậy chi phí cơ hội tại đoạn AB là Ccơ hội = 3
2
09
3024 =
−
−
=
Δ
Δ
luongthuc
quanao
Nhận xét: chi phí cơ hội để sản xuất thêm 01 đơn vị lương thực là 2/3
đơn vị quần áo, nghĩa là để sản xuất thêm 01 đơn vị lương thực thì
người ta mất đi cơ hội sản xuất thêm 2/3 đơn vị hàng hóa.
Các đoạn khác BC, CD, DE làm tương tự
Bài tập 2
Bài này rất đơn giản,
Với nhà kinh doanh:
- Nếu đi máy bay: 700+2*50 = 800 ngàn
- Nếu đi tầu hỏa: 200+18*50 = 1100 ngàn
Vì thế nhà kinh doanh sẽ chọn đi máy bay mặc dù chi phí kế toán
nhìn thấy là 700k lớn hơn 200k.
Tương tự, sinh viên sẽ chọn đi tầu hỏa.
Bài tập 3
Đã chữa tại lớp, bỏ câu e và f, xem qua cho biết cách làm mà thôi
Bài tập 4
Đã chữa, tương tự như bài 3
Bài tập 5
Người tiêu dùng có I=160 (thay lại đầu bài để cho kết quả chẵn hơn)
a. Lợi ích tối đa của người tiêu dùng có thể đạt được là bao nhiêu.
Điều kiện để tối đa hóa lợi ích của người tiêu dùng là
Y
Y
X
X
P
MU
P
MU = và I = X*PX + Y*PY
Mà ta lại có MUX = (TU)’X = (60XY)’X = 60Y
MU
Y = (TU)’Y = (60XY)’Y = 60X
Nên ta có 8
60
4
60 XY = Æ X = 2Y nghĩa là để tối đa hóa lợi ích, thì số
lượng hàng hóa X phải tiêu dùng gấp đôi số lượng hàng Y
Thay vào điều kiện ngân sách ta sẽ có : 160 = 4X + 8Y
Do X = 2Y nên ta có 160 = 16Y Æ Y = 10 Æ X = 5
Vậy thì với ngân sách là I = 160, người tiêu dùng sẽ đạt lợi ích tối đa
nếu tiêu dùng 5 đơn vị hàng X, 10 đơn vị hàng Y
Lợi ích tối đa là : TUMAX = 60XY = 60*5*10 = 3000 đơn vị lợi ích
b. Ngân sách này tăng lên gấp n lần (n>0) và giá cả ko đổi, khi đó
thì tính lại từ đầu, vẫn áp dụng điều kiện tối đa hóa lợi ích để có X
= 2Y, và thay I’ = nI = X*PX + Y*PY nên số lượng hàng hóa tiêu
dùng sẽ là nX, nY và lợi ích sẽ tăng n2.
Chú ý : để có được X = 2Y chỉ xảy ra khi có hàm TU theo X, Y mà
thôi, trường hợp khác sẽ có thay đổi.
c. Ngân sách ko đổi, giá cả thay đổi, cách làm tương tự câu b.
Bài tập 6
áp dụng điều kiệnr
MP
w
MP KL =
Bài tập 8
P 20 24 28 32
QM70 66 62 58
QN80 70 60 50
a. Viết phương trình đường cầu 2 loại hàng trên
Làm như bài 3 với từng loại hàng hóa, chú ý: đây là 2 loại hàng hóa
khác nhau.
b. Cung cố định là 60, cân bằng ntn?
Lúc này phương trình đường cung là : QS = 60, làm như bài tập 3,
quá đơn giản.
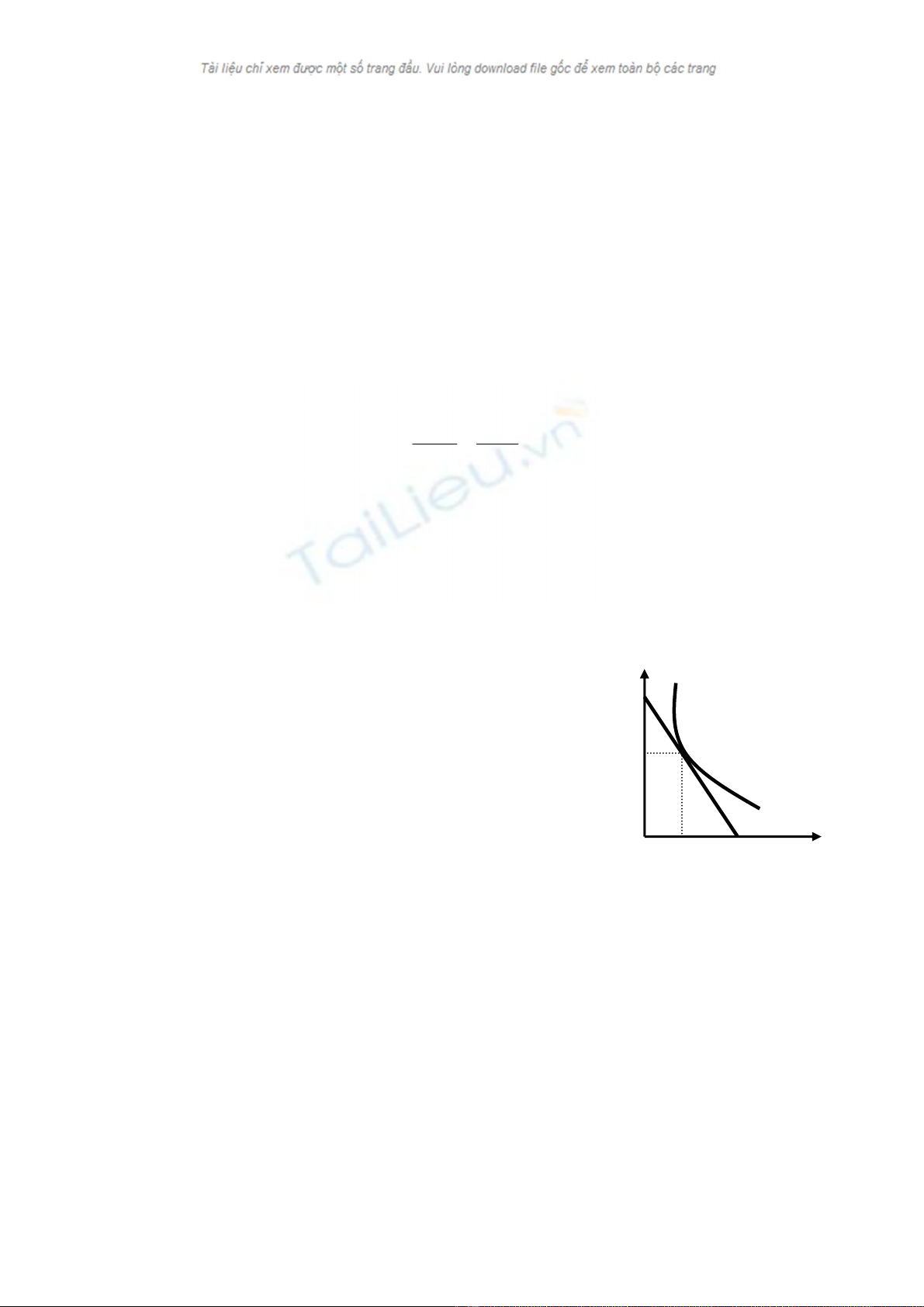
c. Nhận xét về độ dốc của hai đường cầu trên.
Phùng Danh Thắng Đại học TM
Độ dốc nào lớn hơn, nghĩa là độ co dãn của cầu theo giá cũng vì thế
mà khác nhau, và nó thể hiện độ phản ứng của người tiêu dùng trước
sự thay đổi giá cả của hàng hóa. Càng dốc, phản ứng càng mạnh,
Bài tập 9
Bài tập này đã giảng trên lớp, làm bảng 8 cột.
Chú ý, khi ngân sách của người tiêu dùng này thay đổi, giá cả thay
đổi sẽ làm cho lựa chọn tiêu dùng tối ưu sản xuất thay đổi, không
biết chính xác thay đổi bao nhiêu lần, vì thay đổi n lần chỉ đúng khi
có có dạng hàm TU = X.Y. Kết luận là tiêu dùng tối ưu có thay đổi vì
điều kiện tiêu dùng tối ưu là
Y
Y
X
X
P
MU
P
MU = và I = X*PX + Y*PY
Bài tập 10
Làm giống như bài tập 5
Bài tập 11
a. Viết phương trình giới hạn ngân sách
Phương trình đường ngân sách có dạng Y
X
0 80
U
C
80
120
?
I = X*PX + Y*PY
Nếu chỉ tiêu dùng Y thì max được 120 nghĩa
là
X = 0 Æ I = 0*PX + Y*PY = Y*PY
4800 = 120*PY
Æ PY = 40
Nếu chỉ tiêu dùng X thì max được 80 đơn vị nghĩa là
Y = 0 Æ I = X*PX + 0*PY = X*PX
4800 = 80*PX
Æ PX = 60
Như vậy phương trình đường ngân sách là I = 60X + 40Y
Chú ý, nếu người ta nói phương trình giới hạn ngân sách thì nó là
I # 60X + 40Y
b. Xác định số lượng hàng X tại điểm tiêu dùng tối ưu C
Tại điểm tiêu dùng tối ưu thỏa mãn điều kiện