Bµi tËp lín C¶m BiÕn ®o Lêng vµ Xö LÝ TÝn HiÖu
SVTH : Lê Đăng Thắng - Lớp CĐT3 _ K52
Đề Bài 3:Trình bày các hệ thống tín hiệu và hệ thống
cho miền tần số
Bài Làm:
I:Tóm tắt lý thuyết
1.1:Tín hiệu
Định nghĩa : Tín hiệu là một đại lượng vật lý chứa thông tin
(information) có thể truyền đi được. Về mặt toán học tín hiệu được biểu diễn bởi
một hàm hay một biến độc lập
Phân loại tín hiệu : Có 4 loại tín hiệu sau
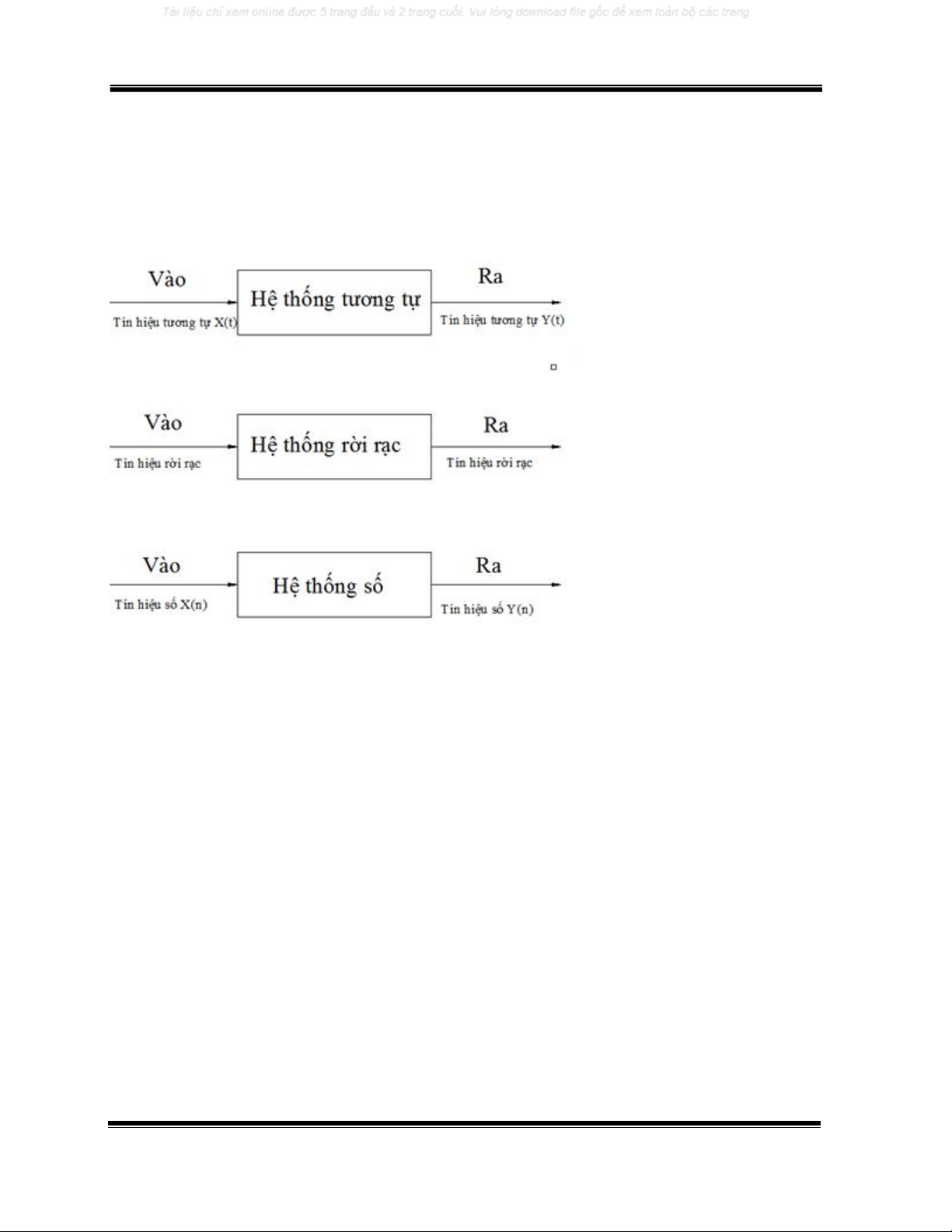
- Tín hiệu tương tự (Analog Signal) : Thời gian liên tục và biên
độ cũng liên tục
- Tín hiệu rời rạc (Discrete Signal) : Thời gian rời rạc và biên độ
liên tục. ( tín hiệu tương tự có sự cách quãng)
- Tín hiệu số ( Digital Signal) : Thời gian rời rạc và biên độ cũng
rời rạc ( loại tín hiệu được mã hóa và có hệ thống xử lý riêng
biệt so với tín hiệu tương tự)
Biểu diễn một số tín hiệu cơ bản :
- Tín hiệu xung đơn vị ( Unit impulse sequence):
δ = δ(n) =
- Tín hiệu hằng ( Constant sequence)
x(n) = A với -∞ < n < +∞
- Tín hiệu nhảy bậc đơn vị (Unit Step sequence):
u(n) =
- Tín hiệu hàm mũ ( Exponetial sequence) :
x(n) : A
- Tín hiệu tuàn hoàn ( Periodic sequence) :
Là một tín hiệu xâu tuần hoàn với chu kì N
1.2. Hệ thống trong miền tần số :
Khái niệm Hệ thống : Lá một thiết bị (device) sử dụng thuật toán
tác động vào tín hiệu đầu vào để cung cấp tín hiệu đầu ra theo một quy luật tính
toán nào đó.
Bản chất là khảo sát được đặc tính cua tín hiệu đó.
Bµi tËp lín C¶m BiÕn ®o Lêng vµ Xö LÝ TÝn HiÖu
SVTH : Lê Đăng Thắng - Lớp CĐT3 _ K52
Định nghĩa theo toán học, đó là một phép quy đổi hay một toán tử
như biến đổi Fourier, Laplace, biến đổi trong miền Z, …
Một số loại hệ thống : hệ thống bất biến theo thời gian, hệ thống
không nhớ, hệ thống tuyến tính,…
Phụ thuộc vào dạng tín hiệu cần xử lý:
Công cụ phân tích tần số:
- Chuỗi Fourier – tín hiệu tuần hoàn
- Biến đổi Fourier – tín hiệu năng lượng, không tuần hoàn
Công cụ tổng hợp tần số :
- Chuỗi Fourier ngược – tín hiệu tuần hoàn
- Biến đổi Fourier ngược – tín hiệu năng lượng, không tuần hoàn
1-3 Phân tích tần sô:
a. Tần số của tín hiệu liên tục thời gian tuần hoàn
x(t) liên tục theo thời gian và tuần hoàn với chu kỳ T p, tần số F0
Phương trình tổng hợp là:
x(t)= 2
o
j kF t
k
k
c e

Bµi tËp lín C¶m BiÕn ®o Lêng vµ Xö LÝ TÝn HiÖu
SVTH : Lê Đăng Thắng - Lớp CĐT3 _ K52
Phng trình tích phân:
0
2
1( )
p
j kF t
k
pT
c x t e
T
Công suất trung bình:
2
| |
x k
k
P c


b,Tần số của tín hiệu liên tục thời gian không tuần hoàn.
x(t) : liên tục và thời gian không tuần hoàn:
2
( ) ( ) j Ft
x t X F e dF


Phương trình tích phân:
2
( ) ( ) j Ft
X F x t e dt


Năng lượng:
2
x
E x t dF


Nếu x(t) là tín hiệu thực thì
( ) ( )
xx xx
S F S F
c- Tần số của tín hiệu rời rạc thời gian tuần hoàn
x(n): rời rạc và tuần hoàn với chu kỳ( x(n+N)=x(n),
n
)
Phương trình tổng hợp:
12
0
( )
k
N
j n
N
k
k
x n c e
Phương trình phân tích:
Bµi tËp lín C¶m BiÕn ®o Lêng vµ Xö LÝ TÝn HiÖu
SVTH : Lê Đăng Thắng - Lớp CĐT3 _ K52
12
0
1( )
k
N
j n
N
kn
c x n e
N
| |
k
j
k k
c c e
Công suất trung bình
1 1
2 2
0 0
1
| ( ) | | |
N N
x k
n k
P x n c
N
Năng lượng trong 1 chu kỳ
1 1
2 2
0 0
| ( ) | | |
N N
x k
n k
E x n N c
d- Tần số của tín hiệu rời rạc thời gian không tuần hoàn.
x(n): rời rạc thời gian va không tuần hoàn:
Phương trình tổng hợp:
2
1
( ) ( )
2
j n
x n X e d
Phương trình phân tích:
( ) ( )
j n
n
X x n e


* *
1 2 1 2
1
( ) ( ) ( ) ( )
2
F
n
x n x n X X d


Năng lượng:
2 2
1
| ( )| | ( )|
2
xn
E x n X d


Phổ mật độ năng lượng:
2 *
| ( ) | ( )
xx
S X X X
1.3 Đặc tính của biến đổi Fourier
Bµi tËp lín C¶m BiÕn ®o Lêng vµ Xö LÝ TÝn HiÖu
SVTH : Lê Đăng Thắng - Lớp CĐT3 _ K52
Đối với tín hiệu rời rạc thời gian và không tuần hoàn, có năng lượng hữu hạn. Và
tín hiệu liên tục thời gian không tuần hoàn có năng lượng hữu hạn.
Tuyến tính: 1 1
2 2
( ) ( )
( ) ( )
F
F
x n X
x n X
1 1 2 2 1 1 2 2
( ) ( ) ( ) ( )
F
a x n a x n a X a X
Dịch theo thời gian:
( ) ( ) ( ) ( )
F F j k
x n X x n k e X
Đảo theo thời gian:
( ) ( ) ( ) ( )
F F
x n X x n X
Tổng chập: 1 1
2 2
( ) ( )
( ) ( )
F
F
x n X
x n X
*
1 2 1 2
( ) ( ) ( ) ( ) ( ) ( )
F
x n x n x n X X X
Tương quan: 1 1
2 2
( ) ( )
( ) ( )
F
F
x n X
x n X
1 2 1 2
0
( ) ( ) ( ) ( )
F Fj k
x x x x
r n S e x n X
Dịch theo tần số:
0
( ) ( ) ( ) ( )
F Fj k
x n X e x n X
Định lý điều chế:
0 0 0
1
( ) () ( ) os ( ) ( )
2
F F
x n X x n c n X X
Định lý Parseval: 1 1
2 2
( ) ( )
( ) ( )
F
F
x n X
x n X