
Hình học lớp 9 - Tiết 45:
LUYỆN TẬP
A. MỤC TIÊU:
- Kiến thức:
- Kĩ năng : Rèn kí năng nhận biết góc có đỉnh ở bên
trong, bên ngoài đường tròn. Rèn kĩ năng áp dụng các
định lí về số đo của góc có đỉnh ở bên trong đường
tròn, bên ngoài đường tròn vào giải 1 số bài tập. Rèn
kĩ năng trình bày bài giải, kĩ năng vẽ hình, tư duy hợp
lí.
- Thái độ : Rèn luyện tính cẩn thận cho HS.
B. CHUẨN BỊ CỦA GV VÀ HS:
- Giáo viên : Thước thẳng, com pa, bảng phụ.

- Học sinh : Thứơc kẻ, com pa.
C. TIẾN TRÌNH DẠY HỌC:
- Ổn định tổ chức lớp, kiểm tra sĩ số HS.
- Kiểm tra việc làm bài tập ở nhà và việc chuẩn bị bài
mới của HS
Hoạt động của GV
Hoạt động
của HS
Hoạt động I
KIỂM TRA (8 phút)
- GV: 1) Phát bi
ểu các
đ
ịnh lí về góc có đỉnh ở
bên trong, góc có đ
ỉnh ở
bên ngoài đường tròn.
2) Chữa bài tập 37
<82 SGK>.
- Một HS lên bảng kiểm
tra.
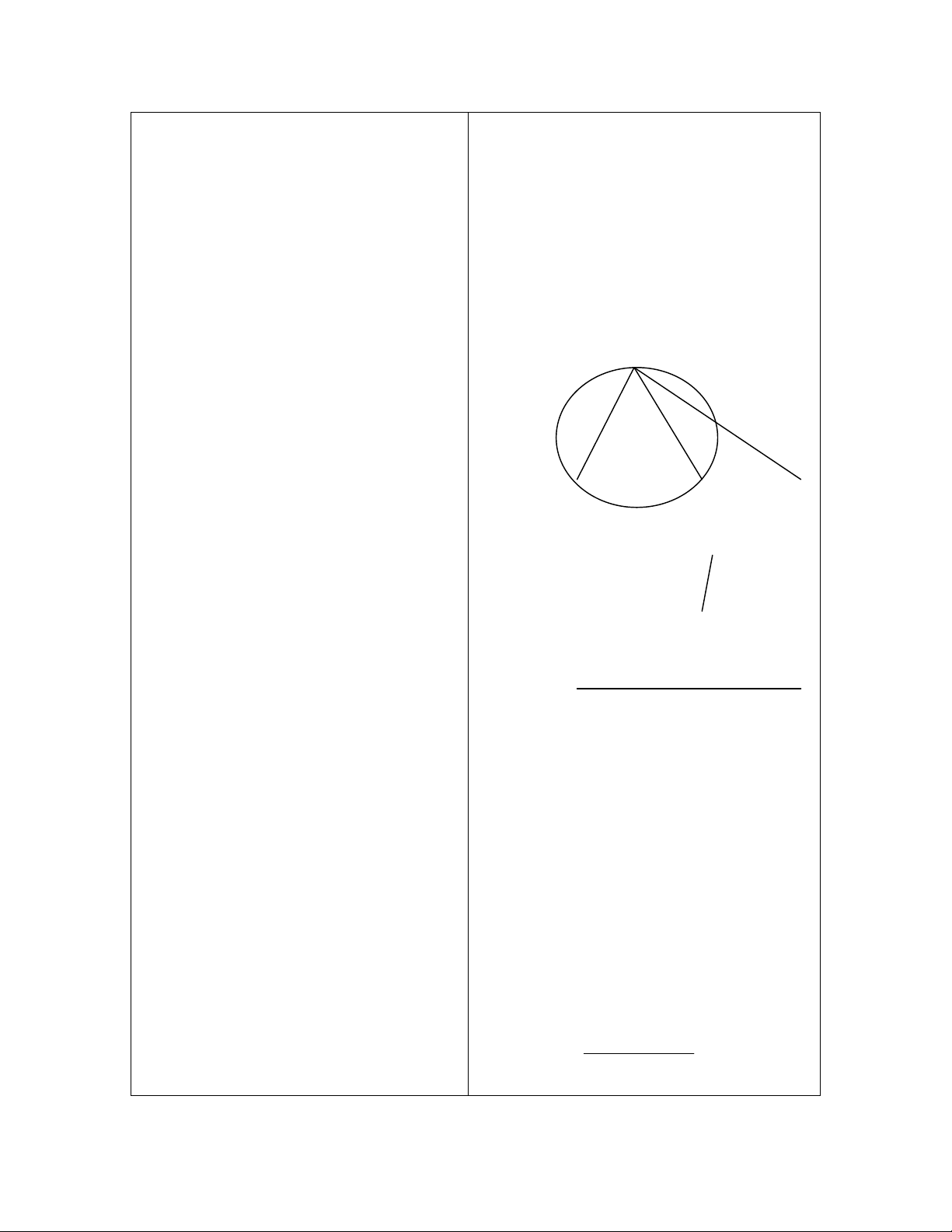
- Bài 37:
A
M
B
C S
- Chứng minh: ASC =
MCA
ASC =
2
SdMCSdAB
(đ/l góc
O
- GV nhận xét, cho điểm.
có đỉnh ở bên ngoài đường
tròn).
MCA =
2
2
SdMCSdACSdAM
Có AB = AC (gt) AB =
AC.
ASC = MCA.
Hoạt động 2
LUYỆN TẬP (35 ph)
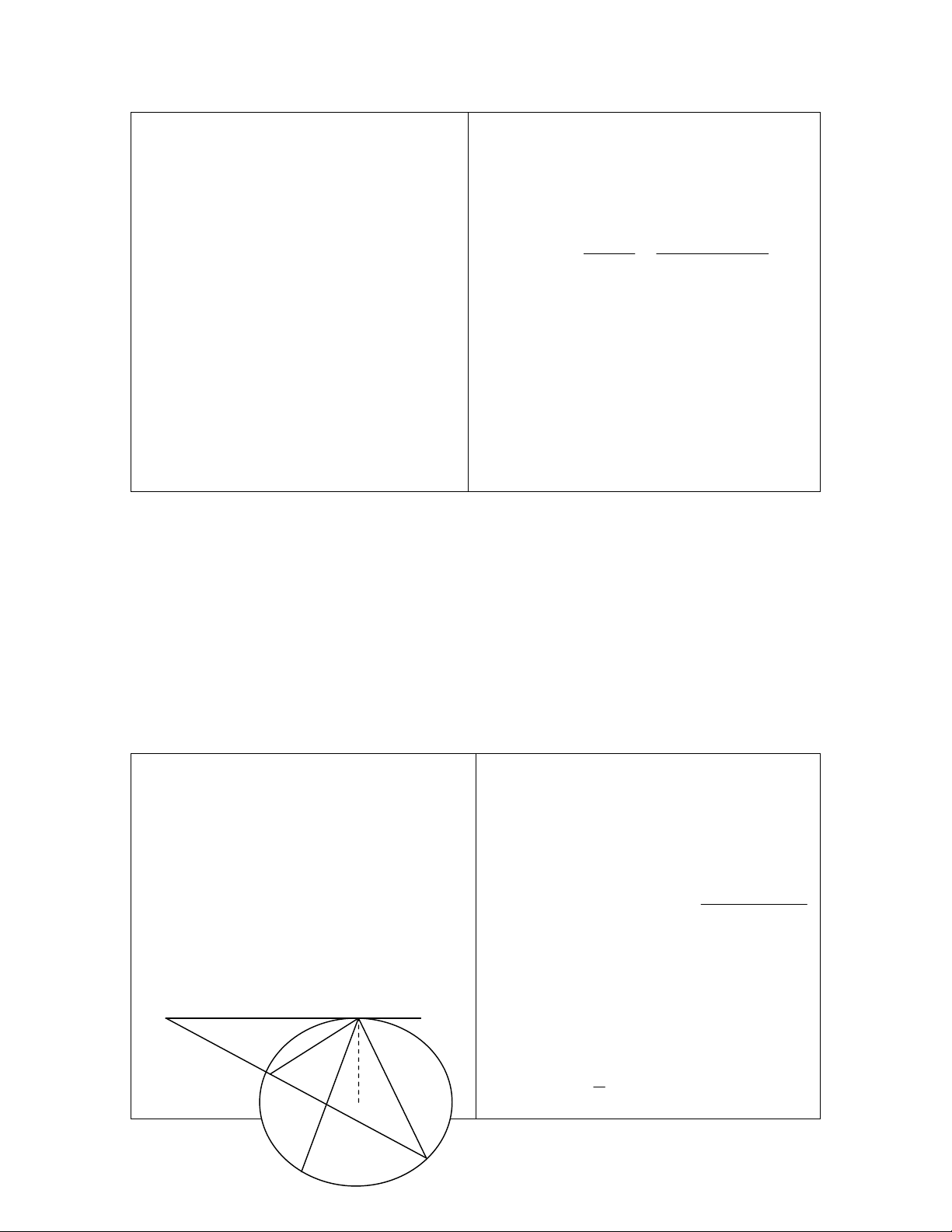
- Chữa bài tập 40 <83
SGK>.
- 1 HS lên vẽ hình.
A
S
- Một HS trình bày bài
giải.
Có: ADS =
2
SdCESdAB
(định lí góc có đỉnh ở
ngoài đường tròn).
SAD =
2
1Sđ AE (đ/l góc
D O
B
E
C
- Yêu cầu HS tìm cách
giải.
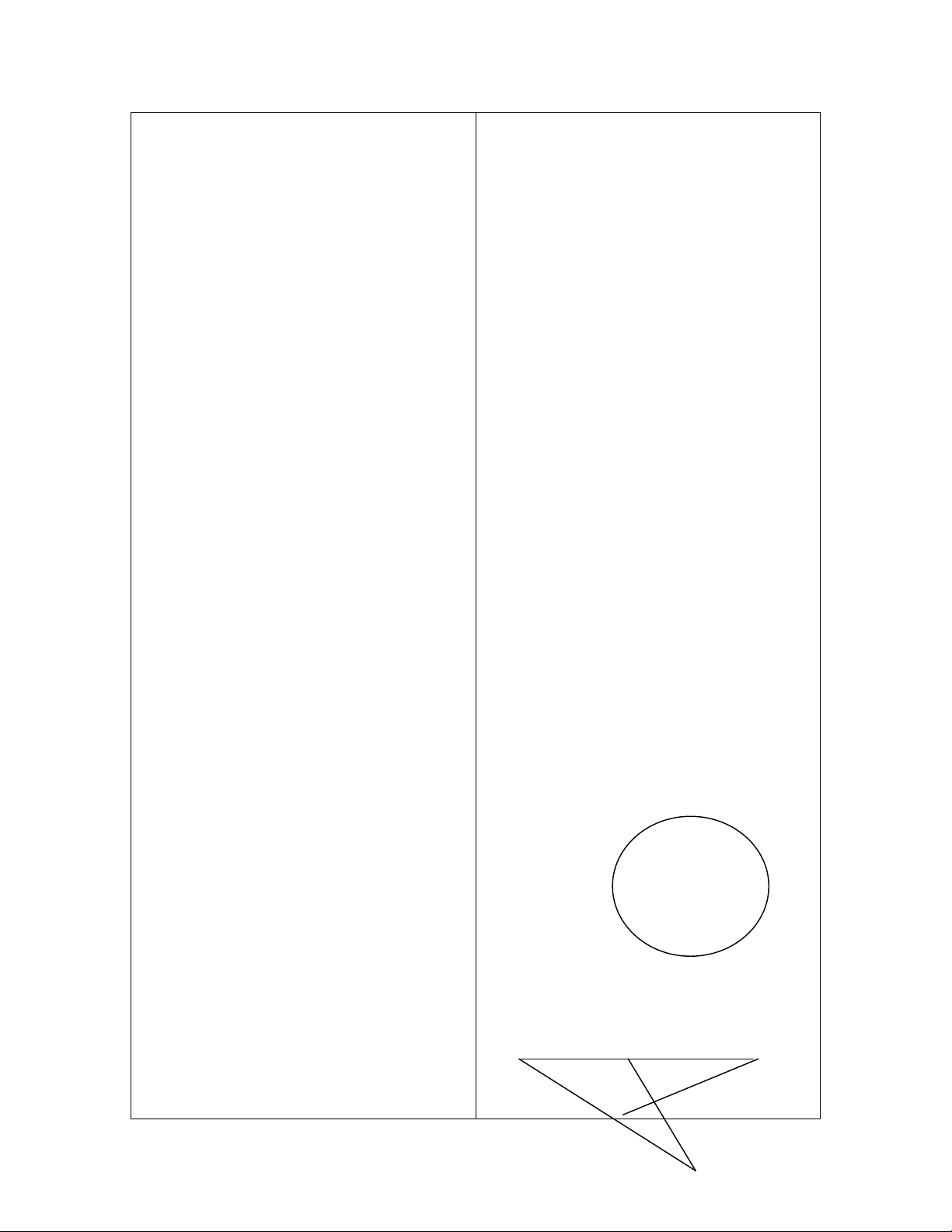
- Yêu cầu HS làm bài 41
<83 SGK>.
giữa tia tiếp tuyến và 1
dây cung).
Có: Â1 = Â2 BE = EC.
Sđ AB + Sđ EC = Sđ
AB + Sđ BE
= Sđ
AE
nên ADS = SAD
SDA cân tại S hay SA =
SD.
- Một HS đọc đề bài, vẽ
hình ghi GT, KL lên
bảng.
A B
C
S
O


























