
I- PH N M ĐUẦ Ở Ầ
1. Lí do ch n đ tài.ọ ề
B i d ng h c sinh gi i là vi c c n thi t, th ng xuyên trong nhàồ ưỡ ọ ỏ ệ ầ ế ườ
tr ng. M i c p h c, m i l p h c v i nh ng yêu c u c th ph i làm sao đóườ ỗ ấ ọ ỗ ớ ọ ớ ữ ầ ụ ể ả
giúp các em có năng khi u nâng cao ki n th c m t cách h th ng theo ch ngế ế ứ ộ ệ ố ươ
trình đc ti p thu trên l p h c hàng ngày.ượ ế ớ ọ
Trong quá trình gi ng d y, b n thân tôi nh n th y m ng ki n th cả ạ ả ậ ấ ả ế ứ
“ph ng trình nghi m nguyênươ ệ ” là m t đ tài lý thú c a S h c và Đi s .ộ ề ủ ố ọ ạ ố
N i dung này đã lôi cu n nhi u ng i, t các h c sinh nh đn các chuyênộ ố ề ườ ừ ọ ỏ ế
gia toán h c l n. Ph ng trình và bài toán v i nghi m nguyên mãi mãi còn làọ ớ ươ ớ ệ
đi t ng nghiên c u c a Toán h c.ố ượ ứ ủ ọ
Ngoài ph ng trình b c nh t hai n, các bài toán tìm nghi m nguyênươ ậ ấ ẩ ệ
th ng không có quy t c gi i t ng quát. M i bài toán v i s li u riêng c a nóườ ắ ả ổ ỗ ớ ố ệ ủ
đòi h i m t cách gi i riêng phù h p. Đi u đó có tác d ng rèn luy n t duyỏ ộ ả ợ ề ụ ệ ư
toán h c m m d o, linh ho t và sáng t o. Chính vì th mà các bài toán tìmọ ề ẻ ạ ạ ế
nghi m nguyên th ng có m t trong các k thi h c sinh gi i v Toán t t cệ ườ ặ ỳ ọ ỏ ề ở ấ ả
các c p. ấ
Trong quá trình b i d ng h c sinh gi i môn toán các kh i 6; 7 và b iồ ưỡ ọ ỏ ố ồ
d ng gi i toán qua m ng l p 9, tôi th y có nhi u bài t p v ch đ ph ngưỡ ả ạ ớ ấ ề ậ ề ủ ề ươ
trình nghi m nguyên khi n nhi u em h c sinh g p không ít khó khăn vì khôngệ ế ề ọ ặ
n m rõ các d ng cũng nh các ph ng pháp gi i chúng. Vì v y, tôi nghiênắ ạ ư ươ ả ậ
c u đ tài ứ ề ‘‘H ng d n h c sinh khá gi i l p 9 gi i ph ng trình nghi mướ ẫ ọ ỏ ớ ả ươ ệ
nguyên hai nẩ" nh m h ng d n các em h c sinh khá gi i có th n m ch cằ ướ ẫ ọ ỏ ể ắ ắ
và gi i t t các bài toán v ph ng trình nghi m nguyên.ả ố ề ươ ệ
* Đi m m i c a đ tàiể ớ ủ ề
Đ tài này h n là đã có m t s tác gi nghiên c u. Song, đi m m i c aề ẳ ộ ố ả ứ ể ớ ủ
đ tài này đó là v n d ng đc nhi u ph ng pháp khác nhau, phân lo iề ậ ụ ượ ề ươ ạ

đc các d ng toán tìm nghi m nguyên, đ tài s d ng m t s bài toán thiượ ạ ệ ề ử ụ ộ ố
h c sinh gi i c p huy n và m t s bài toán trên trang Violympic.vn. Đ phùọ ỏ ấ ệ ộ ố ể
h p v i đi t ng h c sinh, trong đ tài này tôi ch đ c p đn m t sợ ớ ố ượ ọ ề ỉ ề ậ ế ộ ố
ph ng pháp c b n và m t s d ng toán c b n v ch đ ph ng trìnhươ ơ ả ộ ố ạ ơ ả ề ủ ề ươ
nghi m nguyên hai n. Ph ng trình nghi m nguyên có r t nhi u d ng khácệ ẩ ươ ệ ấ ề ạ
nhau v i nhi u cách gi i phong phú khác nhau, vì th trong đ tài này, tôi chớ ề ả ế ề ủ
y u đa ra các ph ng pháp gi i và th hi n qua các ví d đc l y t cácế ư ươ ả ể ệ ụ ượ ấ ừ
tài li u nâng cao môn Toán, t các đ thi h c sinh gi i c p huy n, các bài t pệ ừ ề ọ ỏ ấ ệ ậ
gi i toán qua m ng .....ả ạ
2.Ph m vi áp d ng c a đ tài, sáng ki n, gi i pháp:ạ ụ ủ ề ế ả
Ph m vi nghiên c u c a đ tài là ch đ ph ng trình nghi m nguyênạ ứ ủ ề ủ ề ươ ệ
hai n s trong ch ng trình môn Toán THCS. Trong đ tài này tôi ch nghiênẩ ố ươ ề ỉ
c u các ph ng trình nghi m nguyên v i hai n s .ứ ươ ệ ớ ẩ ố
Đi t ng áp d ng c a đ tài là h c sinh khá, gi i môn Toán l p 9 ố ượ ụ ủ ề ọ ỏ ớ ở
các đn v ( h c sinh tham gia b i d ng gi i toán qua m ng )ơ ị ọ ồ ưỡ ả ạ
II- PH N N I DUNGẦ Ộ
1. Th c tr ng n i dung c n nghiên c uự ạ ộ ầ ứ :
Th c t , qua nhi u năm gi ng d y t i đn v , trong quá trình b i d ngự ế ề ả ạ ạ ơ ị ồ ưỡ
h c sinh gi i, tôi nh n th y h c sinh th ng ng i gi i ph ng trình nghi mọ ỏ ậ ấ ọ ườ ạ ả ươ ệ
nguyên, đc bi t nh ng ph ng trình không d ng m u m c, ph ng trìnhặ ệ ữ ươ ở ạ ẫ ự ươ
nhi u n, nh ng ph ng trình không gi i đc b ng nh ng ph ng phápề ẩ ữ ươ ả ượ ằ ữ ươ
gi i c b n đã đc giáo viên h ng d n. H c sinh th ng lúng túng khi g pả ơ ả ượ ướ ẫ ọ ườ ặ
nh ng ph ng trình có d ng l ho c thoáng nhìn th y có v ph c t p, nh ngữ ươ ạ ạ ặ ấ ẻ ứ ạ ữ
bài toán ki u nh v y làm gi m h ng thú và tính kiên nh n c a trò trong quáể ư ậ ả ứ ẫ ủ
trình h c toán. ọ
Có nhi u nguyên nhân d n đn h c sinh g p khó khăn khi gi i các bàiề ẫ ế ọ ặ ả
toán v ph ng trình nghi m nguyên, trong đó ph i nh c đn nh ng nguyênề ươ ệ ả ắ ế ữ
nhân c b n, đó là: h c sinh không hi u th nào là gi i ph ng trình nghi mơ ả ọ ể ế ả ươ ệ
nguyên, không n m đc cách bi u di n nghi m c a ph ng trình nhi u n,ắ ượ ể ễ ệ ủ ươ ề ẩ
không n m ch c ho c n m không đy đ các ph ng pháp gi i ph ng trìnhắ ắ ặ ắ ầ ủ ươ ả ươ
nghi m nguyên; không phân lo i đc các ph ng trình nghi m nguyên, h cệ ạ ượ ươ ệ ọ
sinh th ng m c m t s sai l m khi gi i ph ng trình nghi m nguyên.ườ ắ ộ ố ầ ả ươ ệ
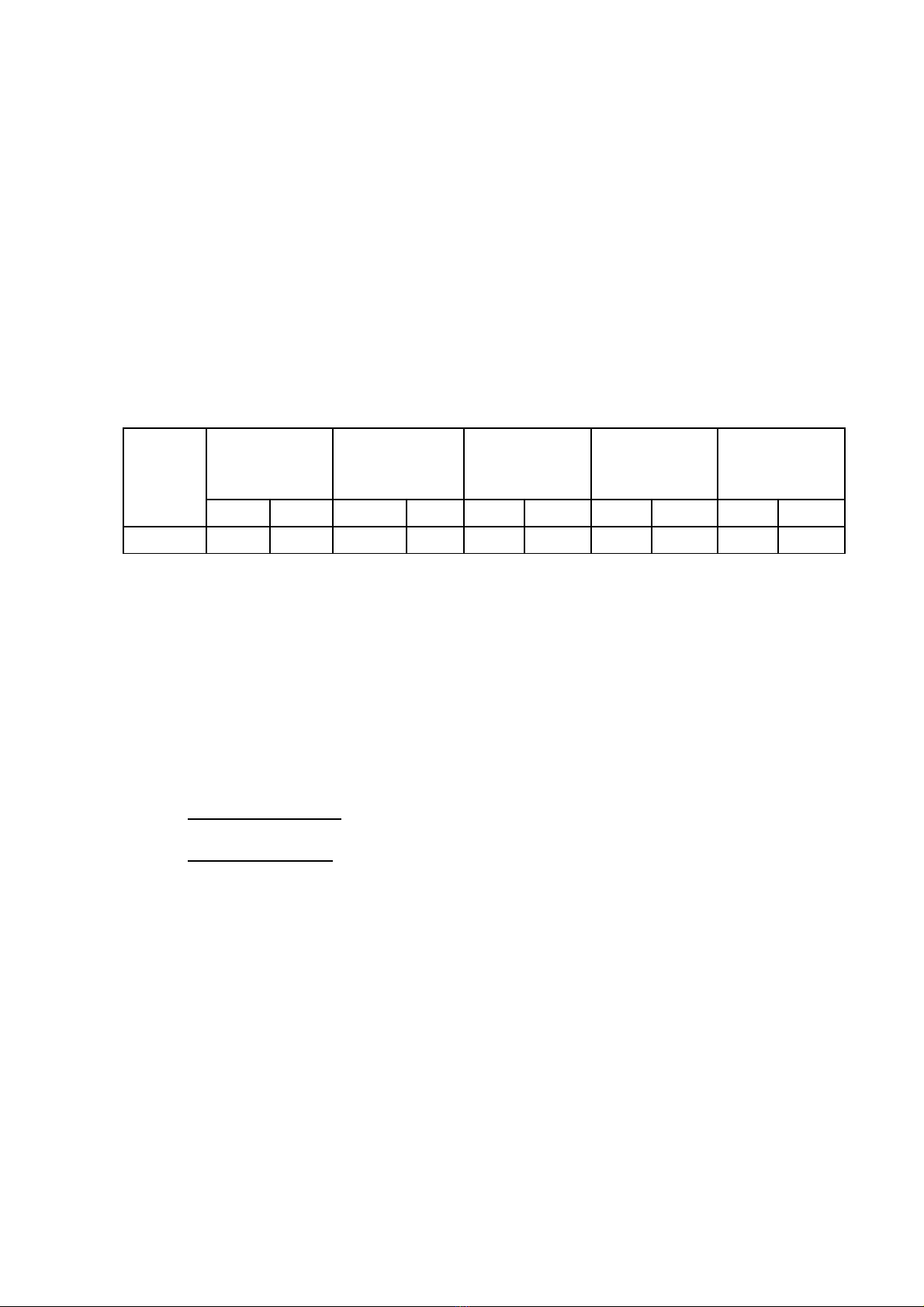
Khi áp d ng đ tài này t i đn v , tôi đã ti n hành kh o sát đi v i điụ ề ạ ơ ị ế ả ố ớ ộ
tuy n b i d ng gi i toán qua m ng l p 9 v ch đ ph ng trình nghi mể ồ ưỡ ả ạ ớ ề ủ ề ươ ệ
nguyên hai n, s li u thu đc nh sau:ẩ ố ệ ượ ư
Lo iạ
đi mể
Không bi tế
cách làm
D i 5,0ướ 5 – 6, 5 6,5 - 8 8 - 10
SL % SL % SL % SL % SL %
SS : 06 02 33,3 03 50,0 01 16,7 0 0 0 0
Tr c th c t đó, tôi m nh d n đ xu t sáng ki n: ướ ự ế ạ ạ ề ấ ế “H ng d n h cướ ẫ ọ
sinh khá gi i l p 9 gi i ph ng trình nghi m nguyên hai nỏ ớ ả ươ ệ ẩ ” v i mongớ
mu n có th giúp đc h c trò c m th y h ng thú h n, t tin h n và gi iố ể ượ ọ ả ấ ứ ơ ự ơ ả
quy t t t h n khi g p các bài toán v ph ng trình nghi m nguyên trongế ố ơ ặ ề ươ ệ
ph ng trình hai n s .ươ ẩ ố
2. Các gi i phápả:
2.1 Gi i pháp 1ả: H ng d n h c sinh n m v ng các khái ni m, ướ ẫ ọ ắ ữ ệ
nh ng thu t ng v ph ng trình nghi m nguyênữ ậ ữ ề ươ ệ
Khi đc đ toán v ph ng trình nghi m nguyên, có nhi u h c sinhọ ề ề ươ ệ ề ọ
không hi u v n đ là gì, tìm nghi m nguyên là nh th nào; m t s khôngể ấ ề ệ ư ế ộ ố
n m đc cách bi u di n nghi m c a ph ng trình nhi u n s ...ắ ượ ể ễ ệ ủ ươ ề ẩ ố
Đ gi i quy t v n đ trên, giáo viên c n ch rõ cho h c sinh thông hi uể ả ế ấ ề ầ ỉ ọ ể
nh ng khái ni m, thu t ng c b n, bi t đc cách bi u di n nghi m c aữ ệ ậ ữ ơ ả ế ượ ể ễ ệ ủ
ph ng trình m t n, ph ng trình hai n.ươ ộ ẩ ươ ẩ
M t s khái ni m, thu t ng c b n, đó là:ộ ố ệ ậ ữ ơ ả

Ph ng trình hai n ươ ẩ là ph ng trình có d ng f(x;y) = 0ươ ạ
Nghi m c a ph ng trình hai n ệ ủ ươ ẩ f(x;y) = 0 là các b s (x; y) th aộ ố ỏ
mãn ph ng trình đó.ươ
Nghi m nguyênệ c a ph ng trình hai n f(x;y) = 0ủ ươ ẩ là các b s nguyênộ ố
(x;y ) th a mãn ph ng trình đã cho.ỏ ươ
Gi i ph ng trình nghi m nguyênả ươ ệ hai n f(x;y) = 0 là tìm t t c cácẩ ấ ả
b s nguyên (x,y) tho mãn ph ng trình đó.ộ ố ả ươ
2.2. Gi i pháp 2ả: Phân lo i các d ng ph ng trình nghi m nguyên.ạ ạ ươ ệ
D ng 1ạ: Ph ng trình b c nh t 2 nươ ậ ấ ẩ
Ví dụ: Tìm nghi m nguyên c a ph ng trình: 12x – 7y = 45 (1)ệ ủ ươ
Gi iả
Ta th y:ấ45 3; 12x 3 nên 7y 3 y 3
Đtặy = 3k (k Z)
Thay vào (1) ta có: 12x – 7 . 3k = 45
4x – 7k = 15
x =
4
1
42
4
715
k
k
k
Đt ặt =
4
1k
(t Z) k = 4t – 1
Do đó x = 2(4t – 1) + 4 – t = 7t + 2
y = 3k = 3(4t - 1) = 12t – 3
V y nghi m nguyên c a ph ng trình đc bi u th b i công th c:ậ ệ ủ ươ ượ ể ị ở ứ
x = 7t + 2
y = 12t – 3
D ng 2ạ: Ph ng trình b c 2 hai nươ ậ ẩ
Ví d 1ụ: Tìm các nghi m nguyên c a ph ng trình:ệ ủ ươ
xy – 2y – 3 = 3x – x2
t Z
Gi iả
Cách 1: Bi u th m t n qua n kia:ể ị ộ ẩ ẩ
y(x - 2) = 3x – x2 +3
D th y: x = 2 không tho mãn ph ng trìnhễ ấ ả ươ
V yậx 2 y =
2
52)2(
2
33 2
x
xxx
x
x
x
= - x + 1 +
2
5
x
Đ y ể Z ta ph i có:ả5 x – 2
V yậ
nghi m nguyên c a ph ng trình là:ệ ủ ươ
(1; - 5); (3; 3); (- 3; 3); (7; - 5)
Cách 2: Đa v ph ng trình c s :ư ề ươ ướ ố
xy – 2y – 3 = 3x – x2
y(x - 2) + x2 – 2x – x + 2 = 5
y(x - 2) + x(x - 2) – (x - 2) = 5
(x – 2) (y + x - 1) = 5
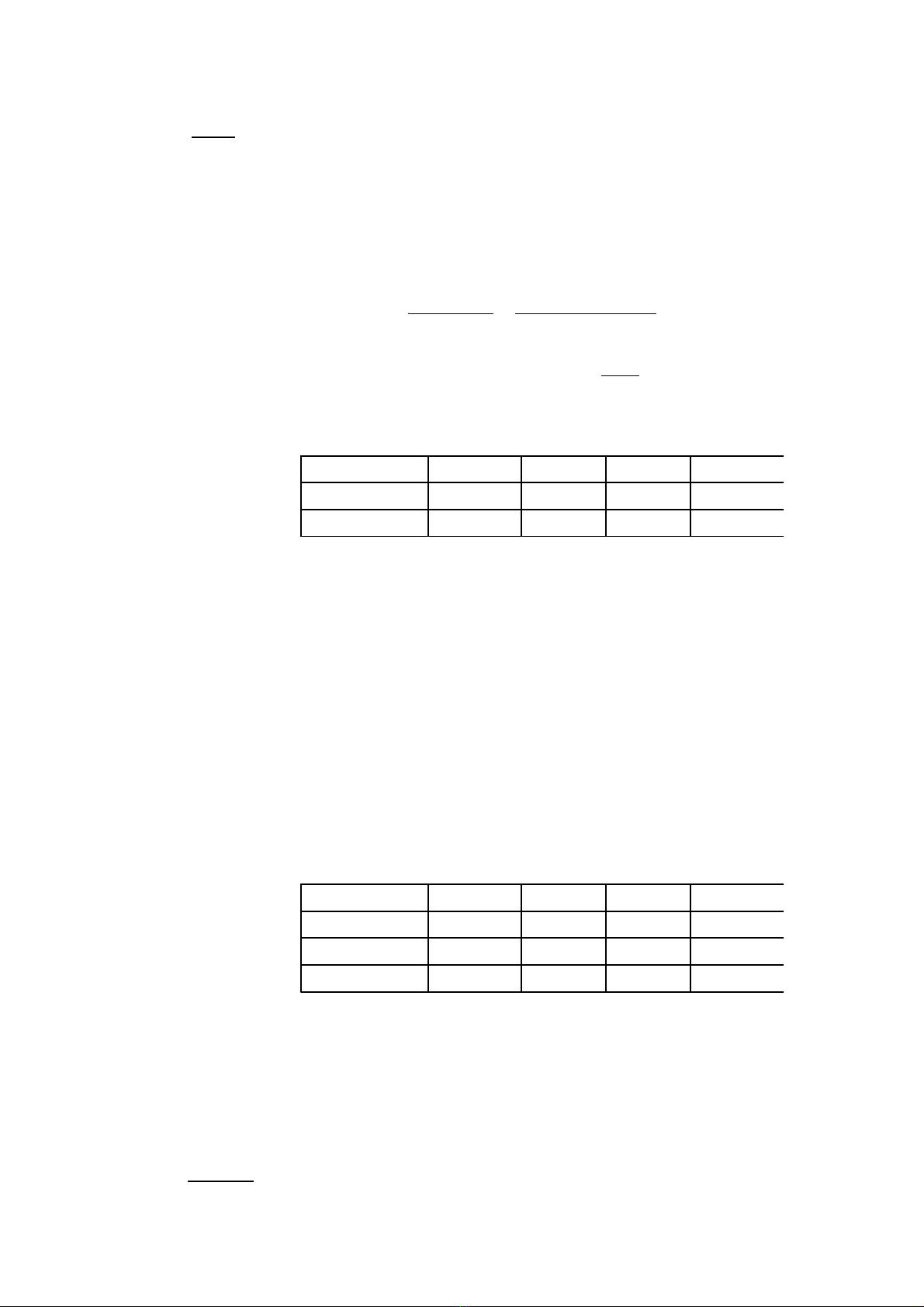
Ta có:
V y nghi m nguyên c a ph ng trình là:ậ ệ ủ ươ
(1; - 5); (3; 3); ( - 3; 3); (7; - 5)
Ví d 2ụ: Tìm các nghi m nguyên c a ph ng trình:ệ ủ ươ
x - 2 - 1 1 - 5 5
y 1 3 - 3 7
x - 5 3 3 - 5
x - 2 - 1 1 - 5 5
x + y - 1 - 5 5 - 1 1
x 1 3 - 3 7
y - 5 3 3 - 5


























