Đề tài: Hướng dẫn học sinh khai thác một
bài tập hình học sách giáo khoa toán 9
I. Đặt vấn đề:
Bắt đầu năm học 2005-2006 học sinh lớp 9 trên toàn quốc được học tập cuốn
sách giáo khoa mới. Trong quá trình giảng dạy bộ môn hình học 9, tôi thấy rằng
cuốn sách được biên soạn khá công phu, sắp xếp hệ thống kiến thức khoa học. Hệ
thống bài tập đa dạng, số lượng bài tập ở trong sách giáo khoa đã quá đủ với tất cả
học sinh. Đặc biệt, các bài tập thử nghiệm đơn giản, nhưng nghiên cứu kĩ tôi thấy
rằng chứa đựng trong đó nhiều điều hết sức thú vị. Cụ thể đó là chúng ta có thể
hướng dẫn các em “khai thác phát triển” thành những bài toán hay hơn khó
hơn…Làm như vậy sẽ góp phần quan trọng trong việc nâng cao năng lực tư duy
cho học sinh, kích thích sự tìm tòi sáng tạo phát huy được trí lực cho học sinh.
II. Nội dung.
Bài toán 1( Bài tập 11 trang 104 SGK - Toán 9 tập 1)
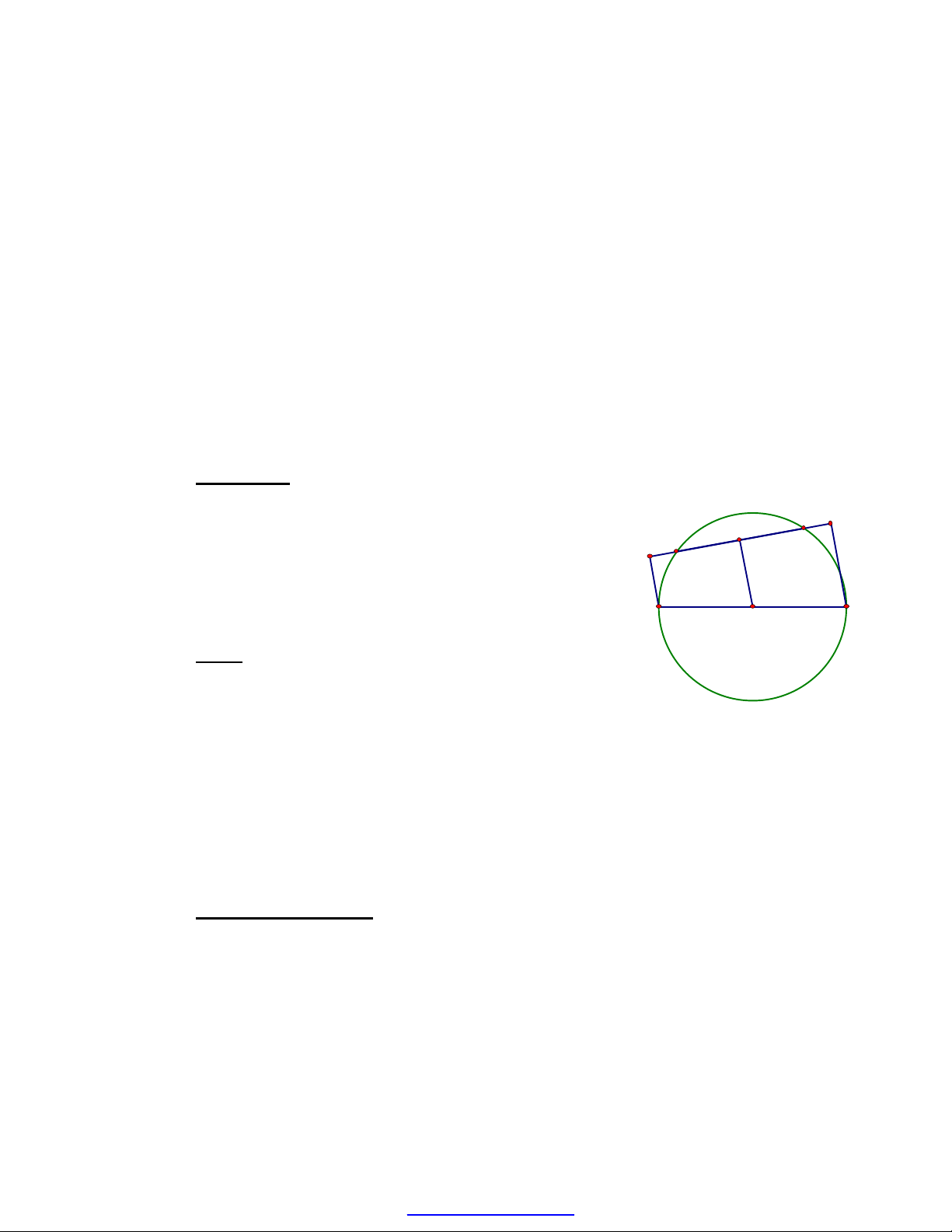
Cho đường tròn (O) đường kính AB, dây CD
không cắt đường kính AB. Gọi H và K theo thứ tự là
chân các đường vuông góc kẻ từ A và B đến CD.
Chứng minh rằng: CH = DK (*)
(Gợi ý: kẻ OM vuông góc với CD).
Giải:
Theo gt ta có: AH
⊥
CD và BK
⊥
CD nên
AH // BK suy ra AHKB là hình thang.
Kẻ OM
⊥
CD tại M
⇒
MC = MD(1)(ĐL quan hệ vuông góc giữa đk và
dây). Xét hình thang AHKB có OA = OB = R; OM//AH//BK (cùng
⊥
CD).
OM là đường trung bình của hình thang
⇒
MH = MK (2)
Từ (1) và (2) ta có CH = DK
Đối với bài tập này ta có thể khai thác theo 2 hướng như sau:
A. Hướng thứ nhất
Để chứng minh CH = DK ta chứng minh hai đoạn thẳng CD và HK có
chung trung điểm. (ở đây ta chỉ xét trường hợp CD và HK thuộc cùng một đường
thẳng nhưng trong trường hợp chúng không cùng một đường thẳng thì CH = DK
vẫn đúng)
- Với ý tưởng chúng ta thử xây dựng một số bài toán mà có thể vận dụng
cách giải ở bài toán (*) để giải nó
MK
H
B
A
O
C
D
PDF created with pdfFactory Pro trial version www.pdffactory.com
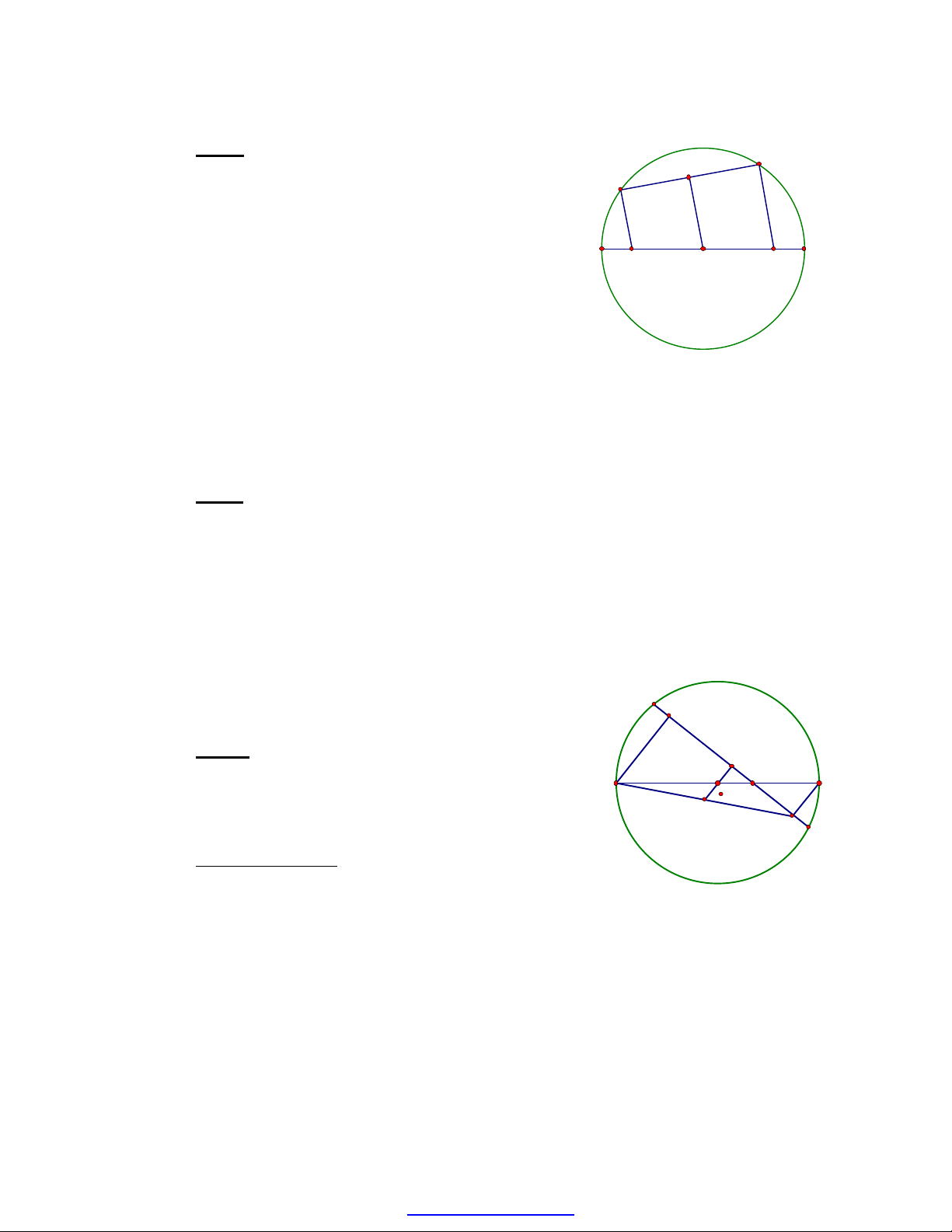
Bài 1:Cho đường tròn O đường kính AB,
dây CD không cắt đường kính. Qua C, D kẻ các
đường vuông góc với CD lần lượt cắt AB tại H
và K.
Chứng minh rằng AH = BK
Để chứng minh AH = BK ta chỉ cần
chứng minh hai đoạn thẳng AB và HK có
chung trung điểm O. Muốn vậy ta làm xuất hiện
trung điểm I của đoạn thẳng CD. Lập luận để
có O là trung điểm của hai đoạn thẳng HK và AB
⇒
ĐPCM
Từ bài toán 1 chúng ta có thể
Phát biểu bài toán đảo như sau:
Bài 2: Bài toán đảo của bài toán 1
Trên đường kính AB của đường tròn tâm O ta lấy hai điểm H và K sao cho
AH = KB. Qua H và K vẽ hai đường thẳng song song với nhau lần lượt cắt đường
tròn tại hai điểm C và D (C, D cùng thuộc một nửa đường tròn tâm O). Chứng
minh rằng: HC ⊥ CD, KD ⊥ CD
Từ bài toán (*) nếu dây cung CD cắt đường kính AB thì kết luận CH = DK
có còn đúng nữa không? Kết luận đó vẫn đúng
và chúng ta có bài toán khó hơn bài toán (*) một
chút như sau.
Bài 3: Cho đường tròn (O) đường kính
AB, dây CD cắt đường kính AB tại G. Gọi H và
K lần lượt là hình chiếu của A và B trên CD.
Chứng minh rằng CH = DK.
Hướng dẫn giải:
Để chứng minh CH = DK ta c/m CD và
HK có chung trung điểm.
Qua O vẽ đường thẳng song song với AH và BK cắt CD tại I, cắt AK tại F.
Lập luận để có OI là đường trung trực của đoạn CD và FI là đường trung
bình của tam giác AHK
⇒
I là trung điểm của HK
⇒
ĐPCM
Cũng là bài toán 3 nhưng chúng ta cũng có thể phát biểu dưới một dạng
khác phức tạp hơn như sau:
KH
I
B
A
O
C
D
F
I
K
H
G
AB
O
C
D
PDF created with pdfFactory Pro trial version www.pdffactory.com
Bài 4: Cho tứ giác ACBD nội tiếp đường tròn đường kính AB. Chứng minh
rằng hình chiếu vuông góc của các cạnh đối diện của tứ giác trên đường chéo CD
bằng nhau. (cách giải hoàn toàn tương tự bài toán 3)
Từ bài toán 3 và 4 ta có thể thấy tam giác AGH nội tiếp đường tròn đường
kính AG, tam giác BGK nội tiếp đường tròn đường kínhBG. Nên từ bài toán 3 & 4
ta có bài toán toán sau
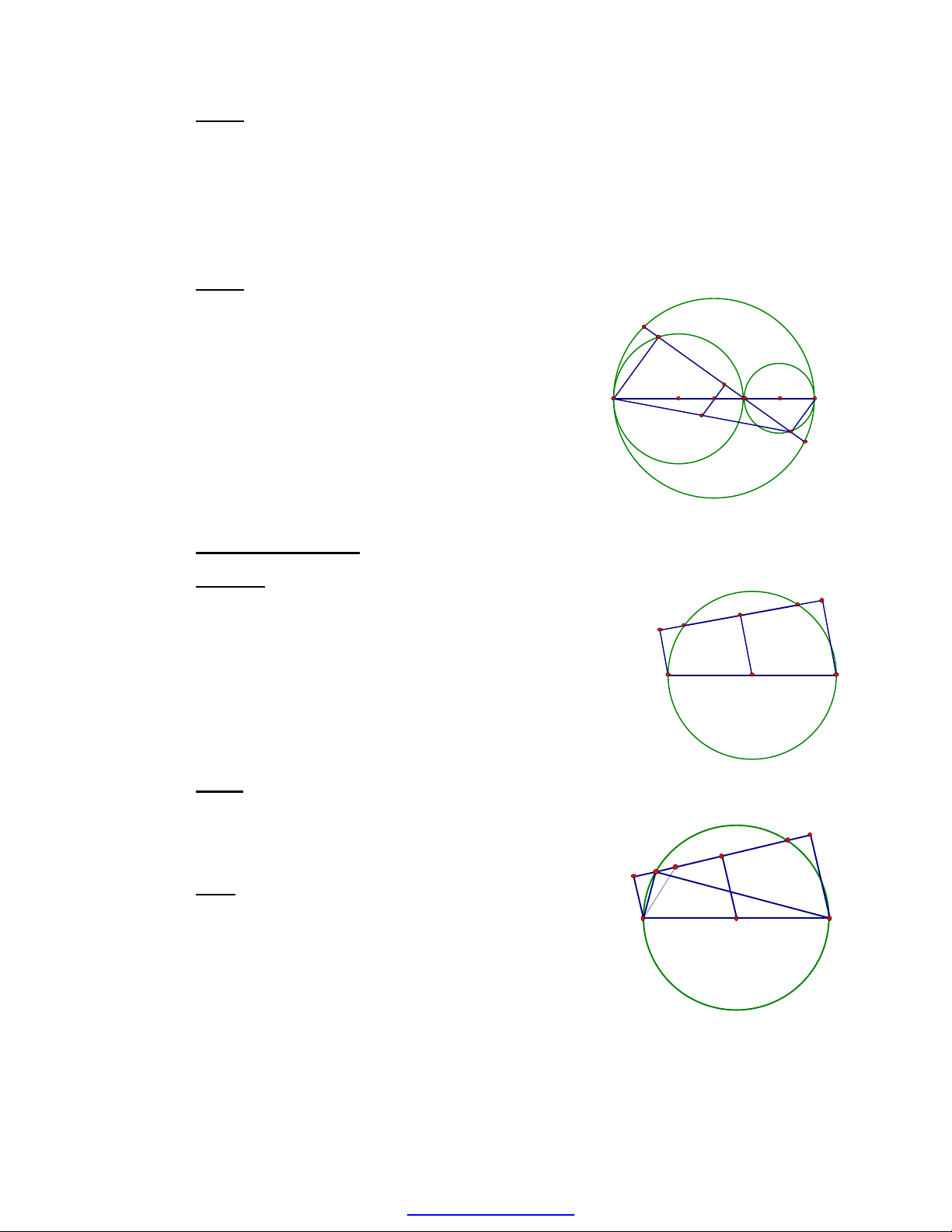
Bài 5: Gọi G là điểm thuộc đoạn thẳng AB
(G không trùng với A và B). Lấy AB, AG và BG
làm đường kính , dựng các đường tròn tâm O,
O1, O2. Qua G vẽ cát tuyến cắt đường tròn (O)
tại C, D; cắt (O1) tại H, cắt (O2) tại K. Chứng
minh CH = DK
B Hướng thứ hai:
Đề bài: ( Bài tập 11 trang 104 SGK - Toán 9
tập 1)
Cho đường tròn (O) đường kính AB, dây CD
không cắt đường kính AB. Gọi H và K theo thứ tự là
chân các đường vuông góc kẻ từ A và B đến CD.
Chứng minh rằng: CH = DK ( gợi ý: kẻ OM ⊥ CD)
Bài 1: Thêm vào bài tập 11 câu b như sau:
Chứng minh H và K ở bên ngoài (O)
Giải: (dùng phương pháp phản chứng)
Giả sử chân đường vuông góc hạ từ A đến
đường thẳng CD là H’, H’ là điểm nằm giữa 2
điểm C và D.
Xét
'
ACH
∆
ta có:
0
ˆˆˆˆ
'90
ACHACBBCDBCD
=+=+
⇒
0
ˆ
'90
ACH >
Mà
0
ˆ
'90
AHC=(theo giả sử)
⇒
Tổng các góc trong của
'
ACH
∆
lớn hơn 1800
là điều vô lí.Vậy H’ phải nằm ngoài đường tròn (O) hay H nằm ngoài (O)
Chứng minh tương tự đối với điểm K
MK
H
B
A
O
C
D
F
I
K
H
D
O1 O2
O
A B
G
C
M
H
K
B
O
A
C
D
H'
PDF created with pdfFactory Pro trial version www.pdffactory.com
C' D'
I
K
H
B
O
A
C
D
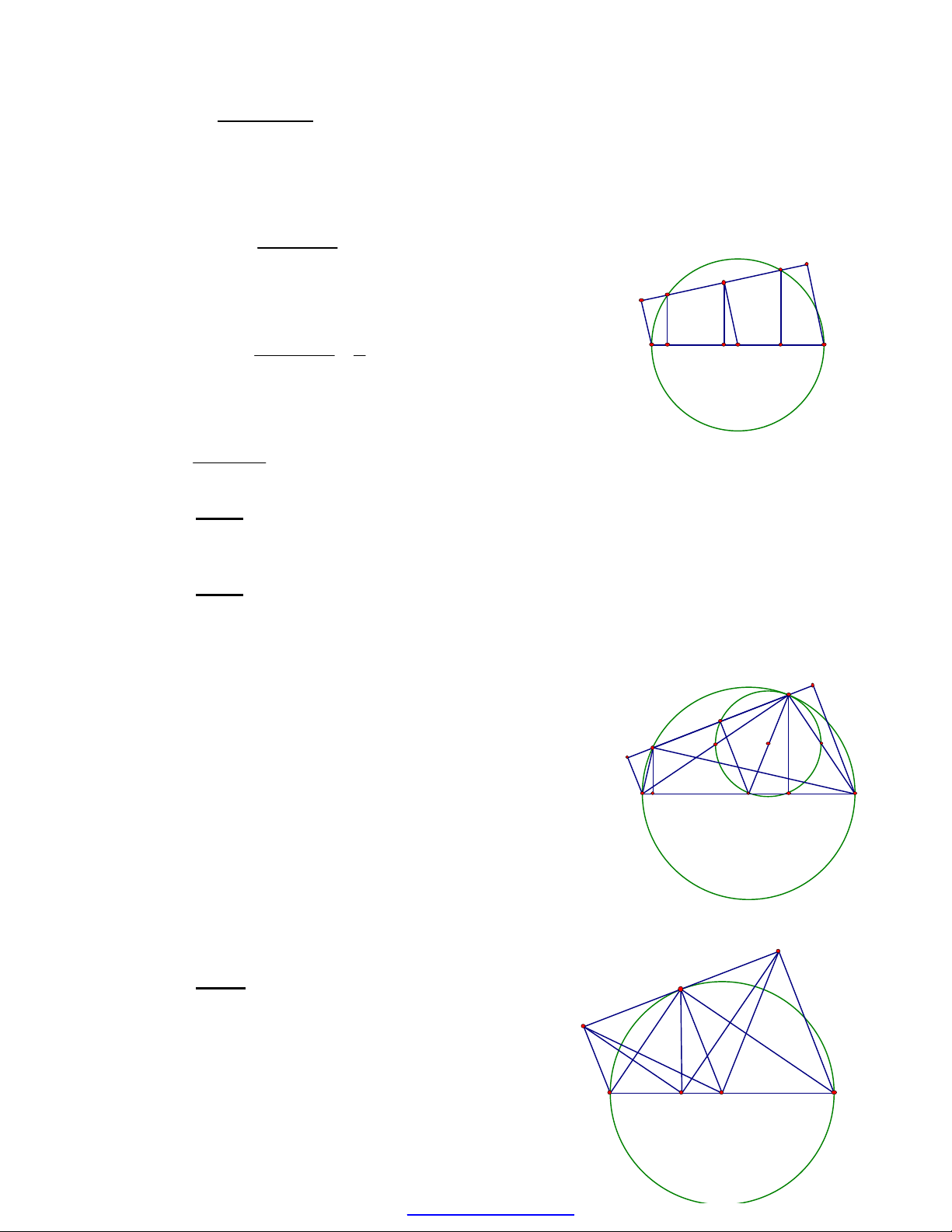
* Nhận xét: Từ việc vẽ OM
⊥
CD ta có MH = MK ta dễ nhận thấy
OMHOMAOMKOMB
SSSS
∆∆∆∆
=== suy ra
HOKAMB
SS
∆∆
= suy ra
HK.OM = AB.MM’ (với MM” ⊥ AB tại M’). Vẽ thêm CC’⊥AB, DD’⊥AB
(C’, D’
∈
AB).
Ta có ''
'
2
CCDD
MM
+
= (MM’ là đường trung
bình của hình thang CDD’C’)
⇒
''1
..('')
22
ACBADB
CCDD
HKOMABABCCDDSS
∆∆
+
==+=+
Mặt khác HK.OM = SAHKB (Vì OM là đường
trung bình của hình thang AHBK nên
2
AHKB
OM
+
=). Từ đó ta có
AHKBACBADB
SSS
∆∆
=+
Bài 2: Qua nhận xét trên ta có thể thêm vào bài 11 câu c:
CMR
AHKBACBADB
SSS
∆∆
=+
Bài 3: Từ nhận xét trên ta lại có bài toán quỹ tích:
a. Tìm quỹ tích trung điểm I của đoạn thẳng CD khi C (hoặc D) chạy trên
đường tròn (O)
b. Tìm quỹ tích điểm H và K khi C (hoặc D) chạy
trên đường tròn tâm O đường kính AB
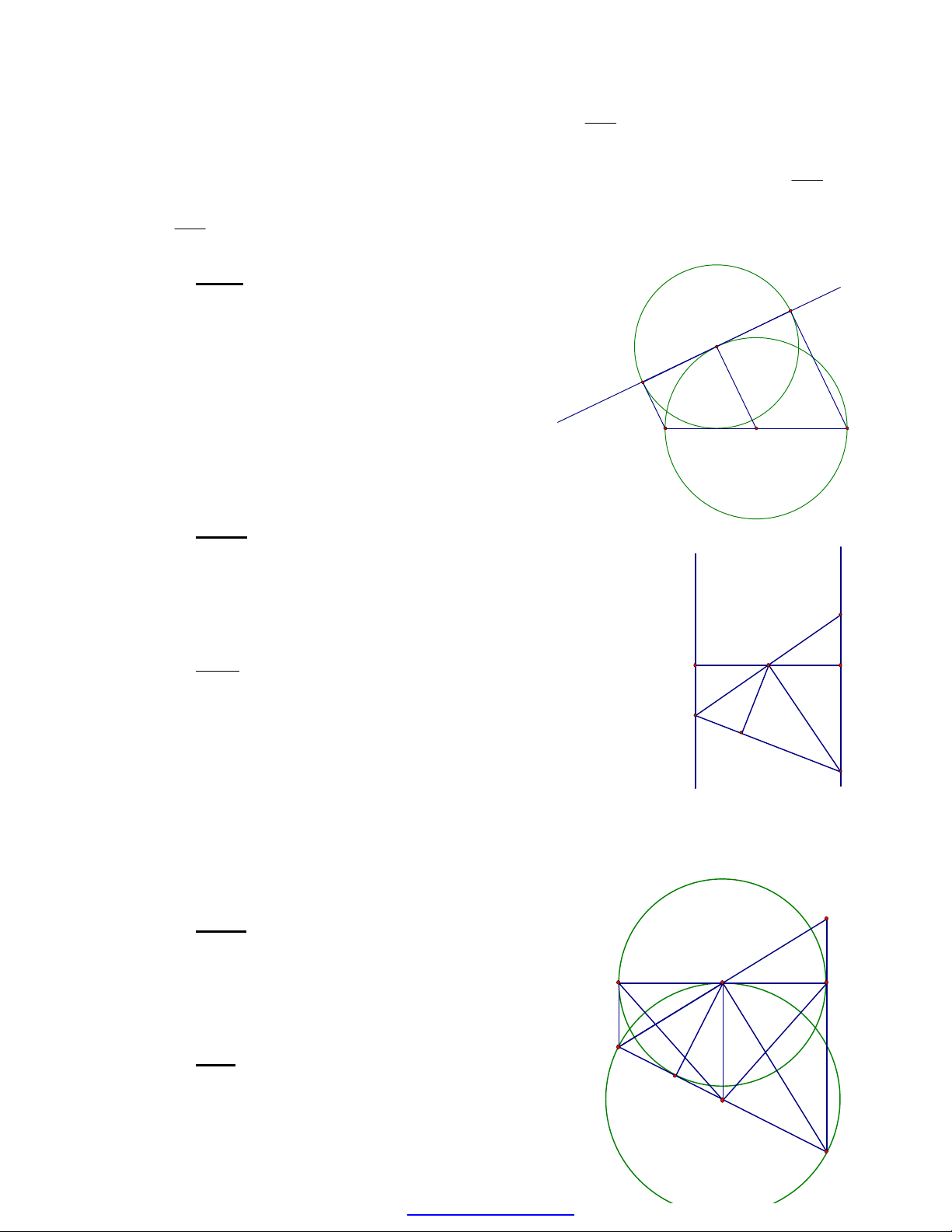
Bài 4: Đặc biệt khi CD không phải là
một dây cung mà CD trở thành tiếp tuyến
của (O) như ở hình bên ta vẫn có S
AMB
∆
=
S
HOK
∆
và HK.OM = AB.MM' (lúc này M
thuộc nửa đường tròn (O)) nên AB = 2.OM.
D'M'C'
M
H
K
B
O
A
C
D
M'
H
K
B
O
A
M
PDF created with pdfFactory Pro trial version www.pdffactory.com
Do đó ta có HK.OM = 2.OM.MM' '
2
HK
MM⇒=
Dựa vào điều kiện một điểm thuộc đường tròn ta có M'
(;)
2
HK
M∈
⇒
(;)
2
HK
M tiếp xúc với AB tại M'
Bài 5: Từ bài 4 ta có bài 5
Cho đường tròn (O) đường kính AB,
M là một điểm bất kì trên nửa đường tròn đó
(M ≠ A và B). Qua M vẽ tiếp tuyến xy, H
và K là chân các đường vuông góc hạ từ A,
B xuống xy. Chứng minh rằng : đường tròn
(M) đường kính HK tiếp xúc với AB
(Xác định vị trí tương đối của (M) với
đường thẳng AB khi M chạy trên (O)).
Bài 6
: Cho một đoạn thẳng HK, qua
H, K vẽ các đường thẳng d và d’ vuông góc với HK. Một
góc vuông với đỉnh là trung điểm M của HK có một cạnh
cắt d tại A, một cạnh cắt d’ tại B. Chứng minh rằng AB là
tiếp tuyến của đường tròn đường kính HK.
Giải:
Vẽ MD
⊥
AB (1)
()
DAB
∈
. Gọi
'
CAMd
=∩
Ta có
AMHCMK
∆=∆
(g-c-g)
MAMC
⇒=
⇒
ABC
∆
có BM vừa là
đường cao, vừa là trung tuyến nên
ABC
∆
cân tại B
BM
⇒
là phân giác của
·
ABC
·
·
ABMCBM
⇒=
MDBMKB
⇒∆=∆
(cạnh huyền - góc nhọn)
MDMK
⇒=
mà
MH = MK = HK/2 (2)
Từ (1) & (2) suy ra AB là tiếp tuyến của
đường tròn đường kính HK.
Bài 7: Cho tứ giác AHKB có đường tròn
đường kính AB tiếp xúc với đường thẳng HK.
Chứng minh rằng đường tròn đường kính HK
tiếp xúc với đường thẳng AB khi và chỉ khi AH//
BK.
Giải: Gọi O và O' lần lượt là trung điểm
của AB và HK
dd'
D
B
C
M
HK
A
a
b
O
C
B
A
O'
HK
D
x
yK
H
B
O
A
M
PDF created with pdfFactory Pro trial version www.pdffactory.com


























