
PHƯƠNG PHÁP SỐ
TRONG CÔNG NGHỆ HÓA
HỌC
Mã học phần: CH3454
TS. Nguyễn Đặng Bình Thành
BM:Máy & TBCN Hóa chất
Numerical Methods in Chemical Engineering
Tuần 5
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Nghi m th c c a ph ng trình – Ý nghĩa hình h c.ệ ự ủ ươ ọ
f(x) = 0; ( 1 )
f – hàm cho tr c c a đ i s xướ ủ ố ố
α - nghi mệ th cự c aủ ( 1 )
f(α) = 0; ( 2 )
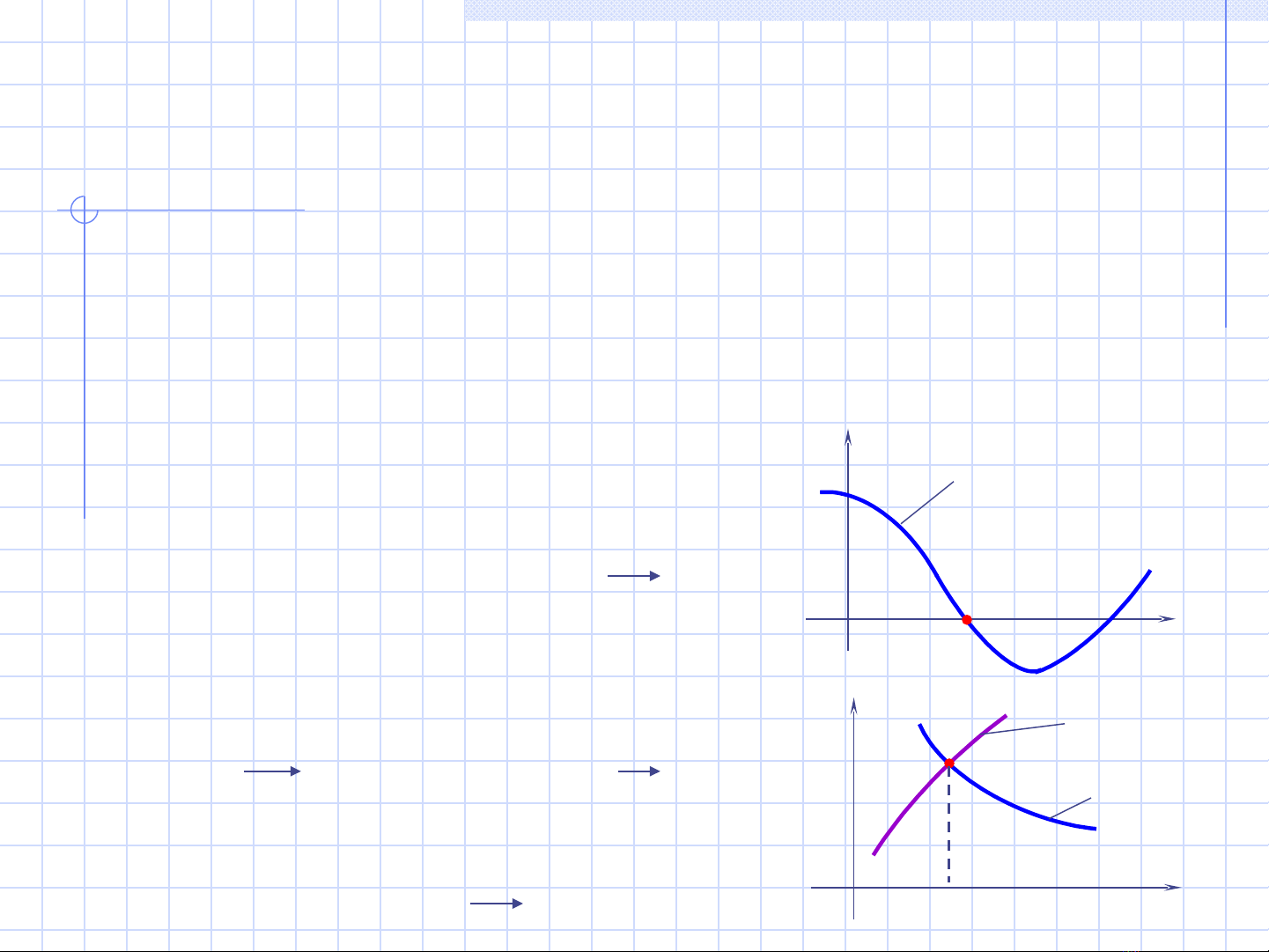
- V đ th y = f(x) ẽ ồ ị
Hoành đ đi m M nghi m ộ ể ệ α.
O
y
x
α
M
f(x)
O
y
x
M
α
g(x)
h(x)
~ g(x) = h(x)
đ th yồ ị 1 = g(x) và y2 = h(x)
- ho c (1)ặ
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
S t n t i c a nghi m th cự ồ ạ ủ ệ ự
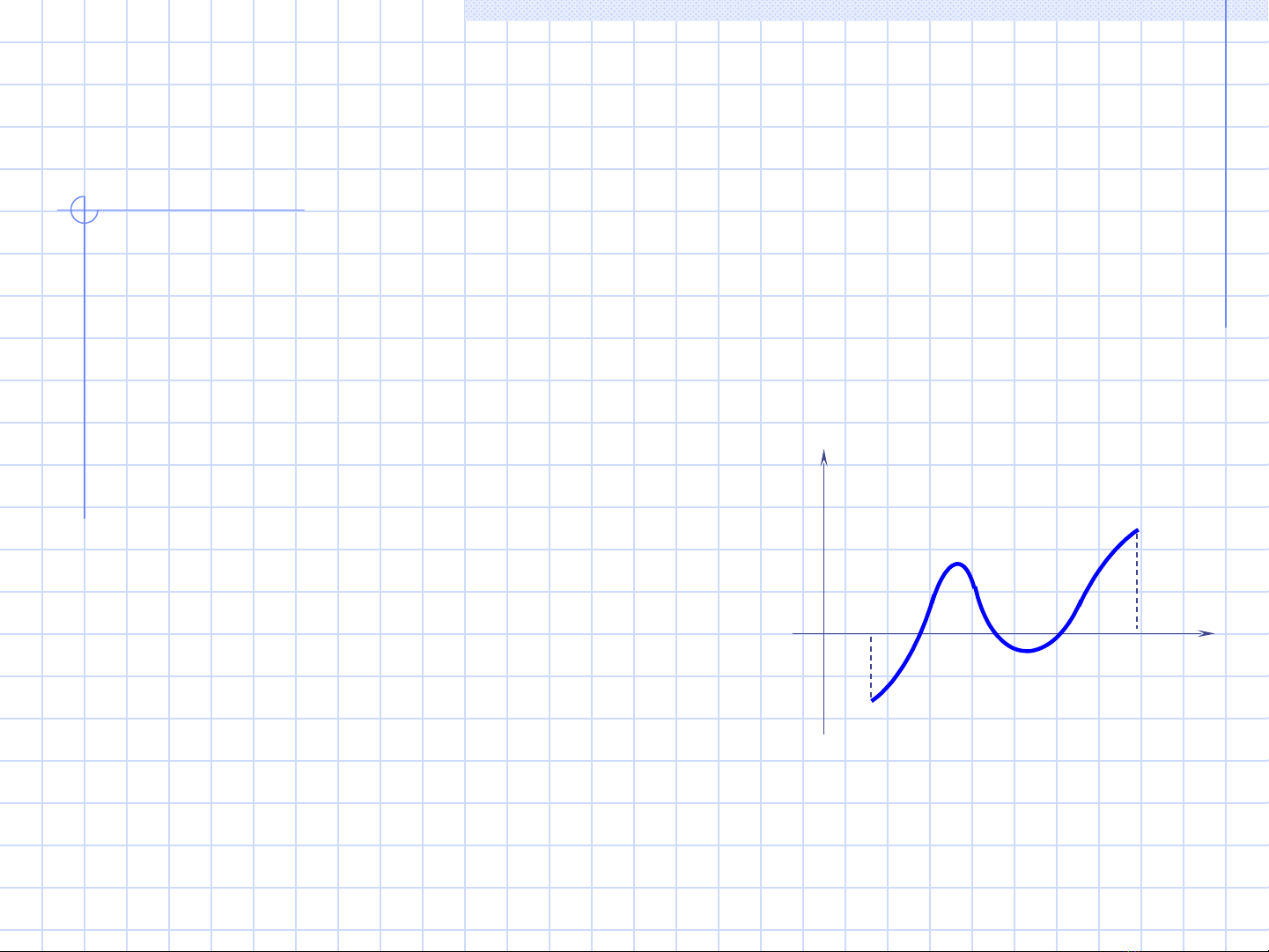
Đ nh lýị. N u có hai s th c a, b ế ố ự
(a < b) sao cho f(a) và f(b) trái
d u, t c làấ ứ
f(a).f(b) < 0 ( 3 )
đ ng th i f(x) liên t c trên [a, b] ồ ờ ụ
thì trong kho ng [a, b] ít nh t cóả ấ
m t nghi m th c c a ph ng ộ ệ ự ủ ươ
trình f(x) = 0.
O
y
x
A
B
a
b
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Kho ng phân ly nghi m (tách nghi m)ả ệ ệ
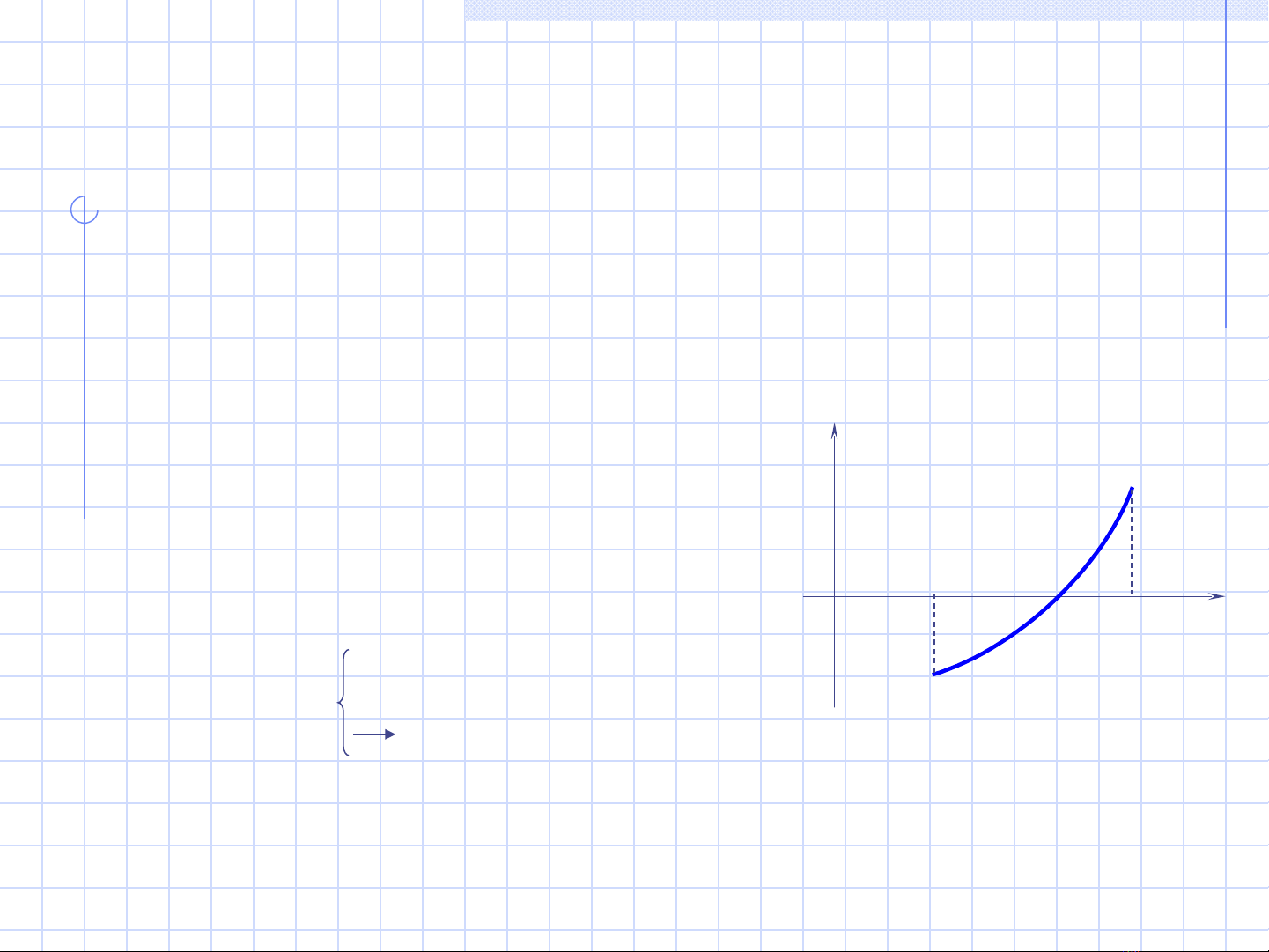
Đ nh nghĩaị: Kho ng [a, b] nào ả
đó g i là kho ng phân ly nghi m ọ ả ệ
c a ph ng trình f(x) = 0 n u nó ủ ươ ế
ch a m t và ch m t nghi m ứ ộ ỉ ộ ệ
c a ph ng trình đó.ủ ươ
trong [a, b] : - hàm f(x) đ n đi uơ ệ
O
y
x
A
B
a
b
f’(x) không đ i d uổ ấ
Đ nh lýị: N u hàm s f(x) liên t c và đ n đi u trên kho ng [a, b], ế ố ụ ơ ệ ả
đ ng th i f(a) và f(b) trái d u thì [a, b] là kho ng phân ly nghi m ồ ờ ấ ả ệ
c a ph ng trình f(x) = 0.ủ ươ

Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Các ph ng pháp xác đ nh g n đúng nghi m th c c a ươ ị ầ ệ ự ủ
ph ng trình phi tuy nươ ế
1. Ph ng pháp đ th .ươ ồ ị
2. Ph ng pháp th .ươ ử
3. Ph ng pháp chia đôi.ươ
4. Ph ng pháp l pươ ặ .
5. Ph ng pháp ti p tuy nươ ế ế
(ph ng pháp Newton-Raphson).ươ
6. Ph ng pháp dây cung.ươ


























