
PHƯƠNG PHÁP SỐ
TRONG CÔNG NGHỆ HÓA
HỌC
Mã học phần: CH3454
TS. Nguyễn Đặng Bình Thành
BM:Máy & TBCN Hóa chất
Numerical Methods in Chemical Engineering
Tuần 6
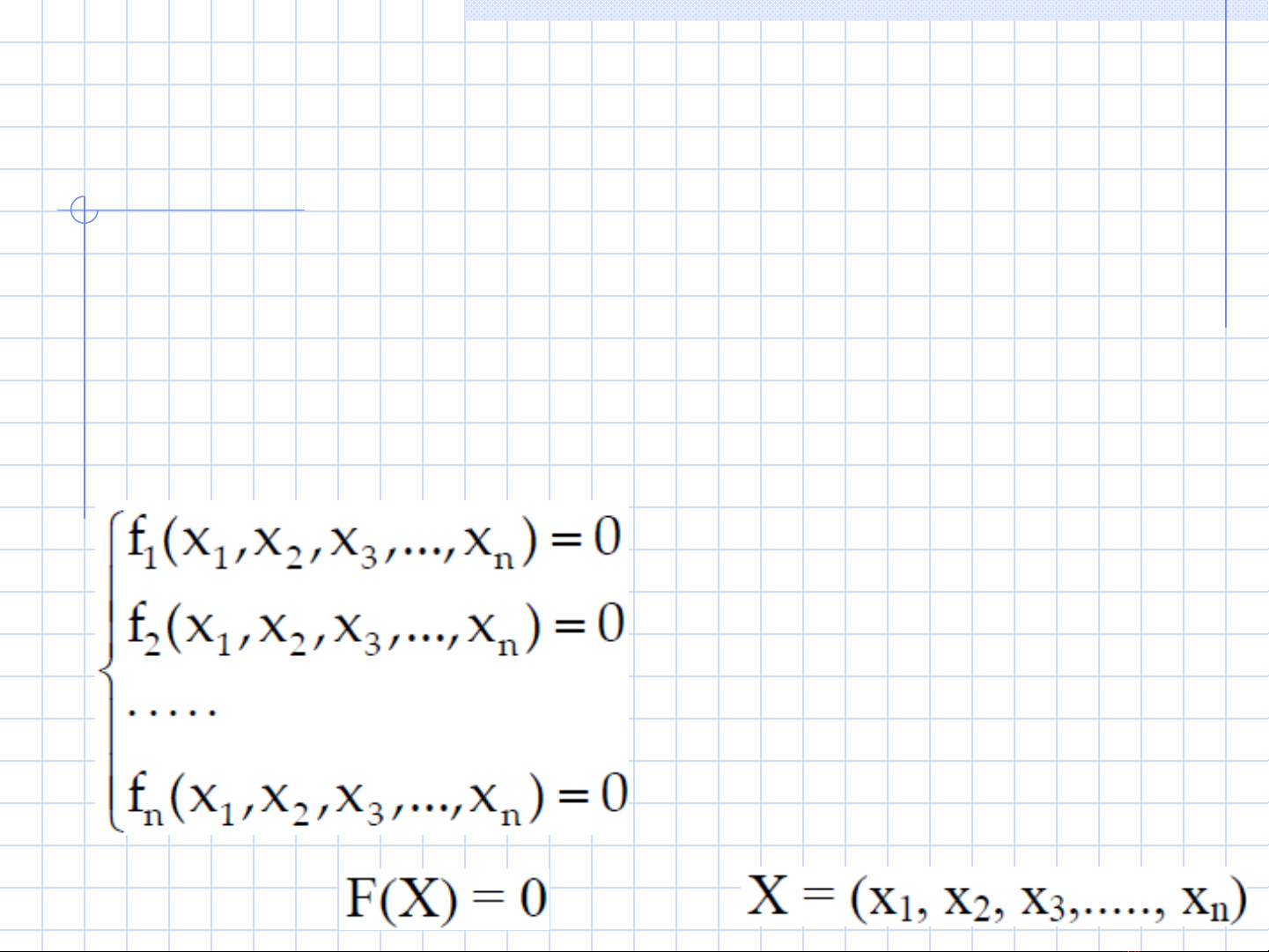
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Gi i h ph ng trình phi tuy n b ng ph ng pháp Newtonả ệ ươ ế ằ ươ
Phương pháp Newton có thể tổng quát hóa để giải hệ phương trình phi
tuyến có dạng:
Dạng ma trận: Trong đó:
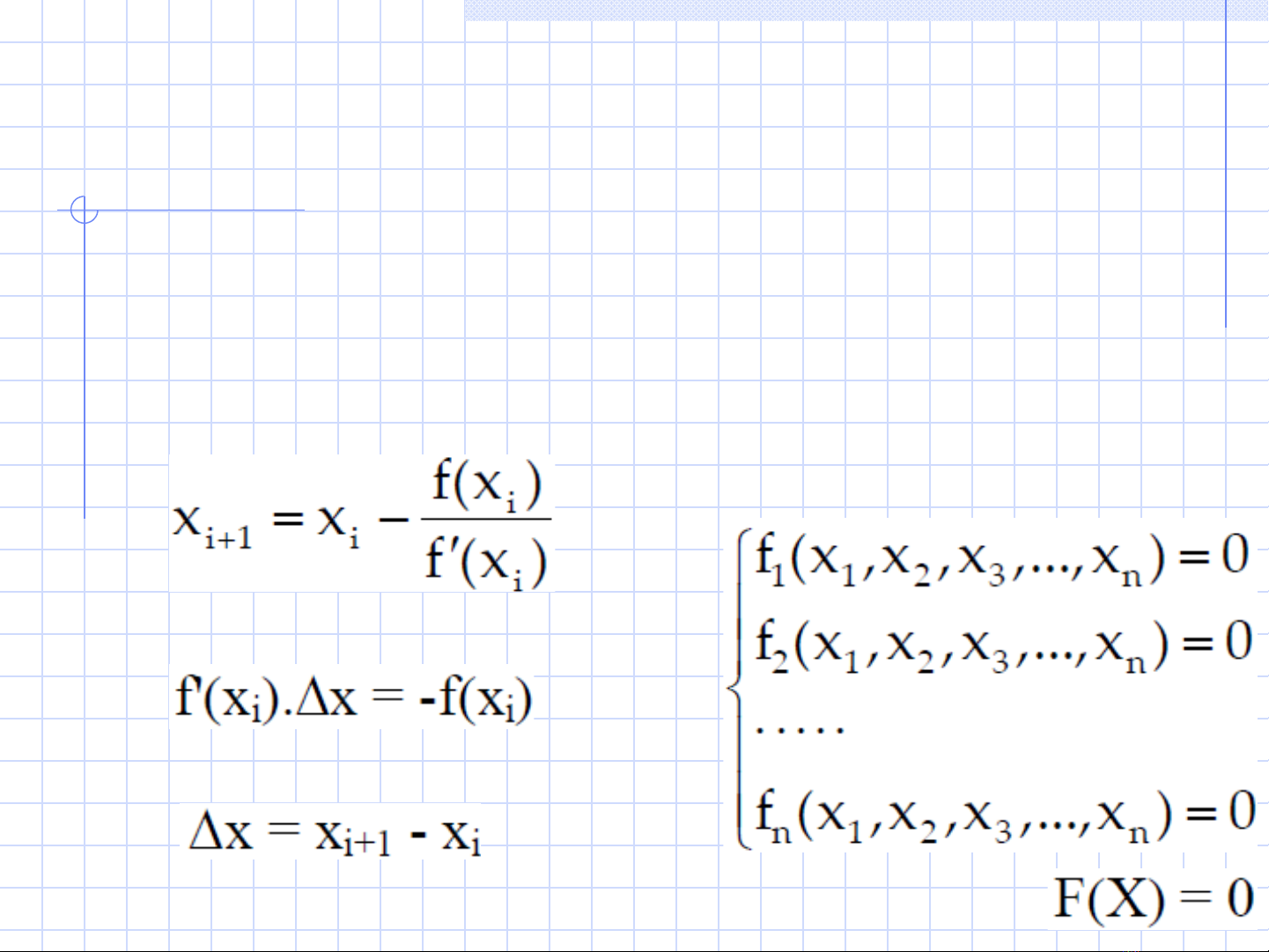
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Gi i h ph ng trình phi tuy n b ng ph ng pháp Newtonả ệ ươ ế ằ ươ
Công thức Newton với phương trình 1 biến:
Hay:
Với:
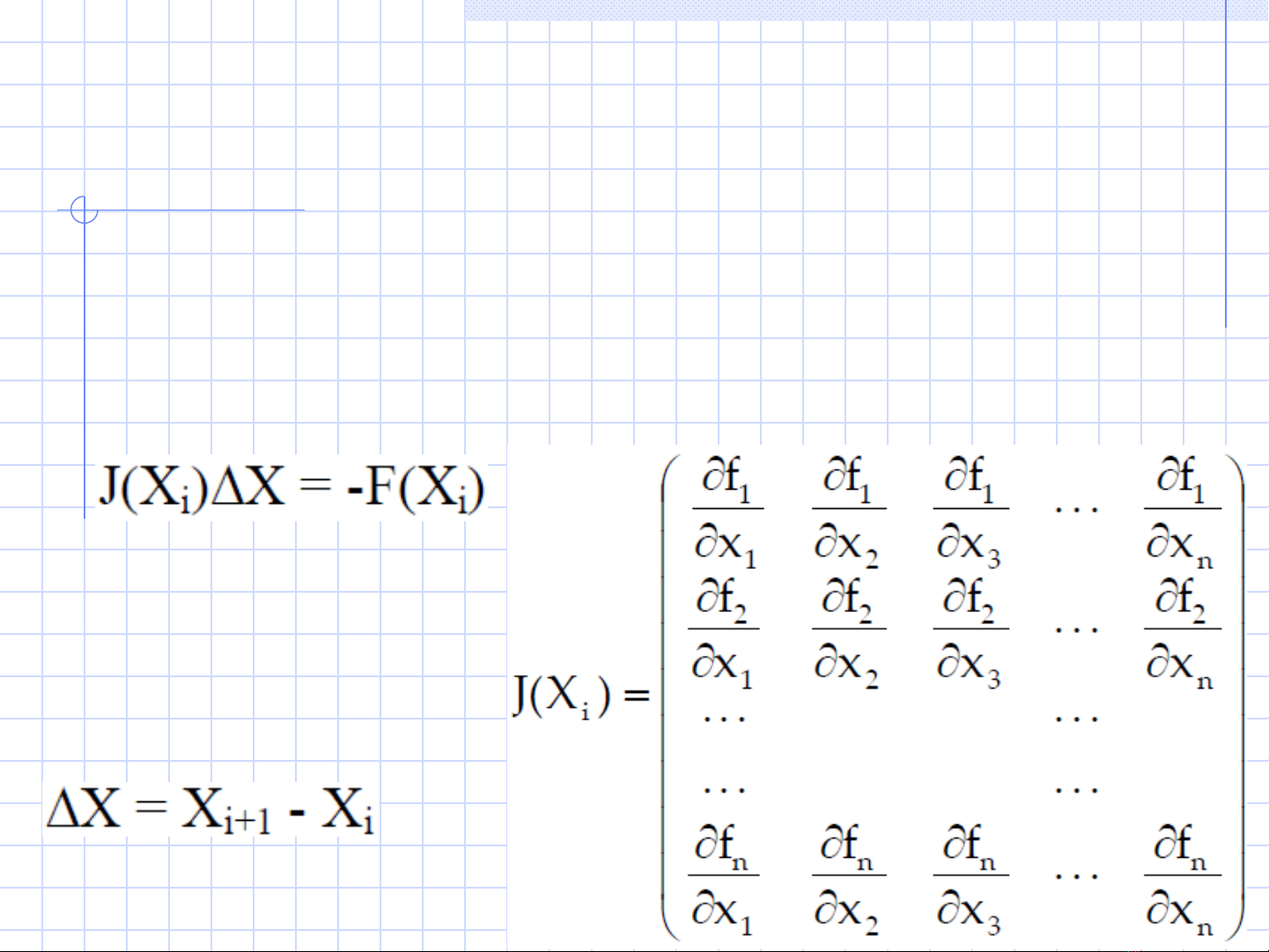
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Gi i h ph ng trình phi tuy n b ng ph ng pháp Newtonả ệ ươ ế ằ ươ
Đối với hệ phương trình phi tuyến, công thức Newton tổng quát:
Trong đó J(Xi) là ma trận
(toán tử) Jacobi. Nó là ma
trận cấp n có dạng:
Và:
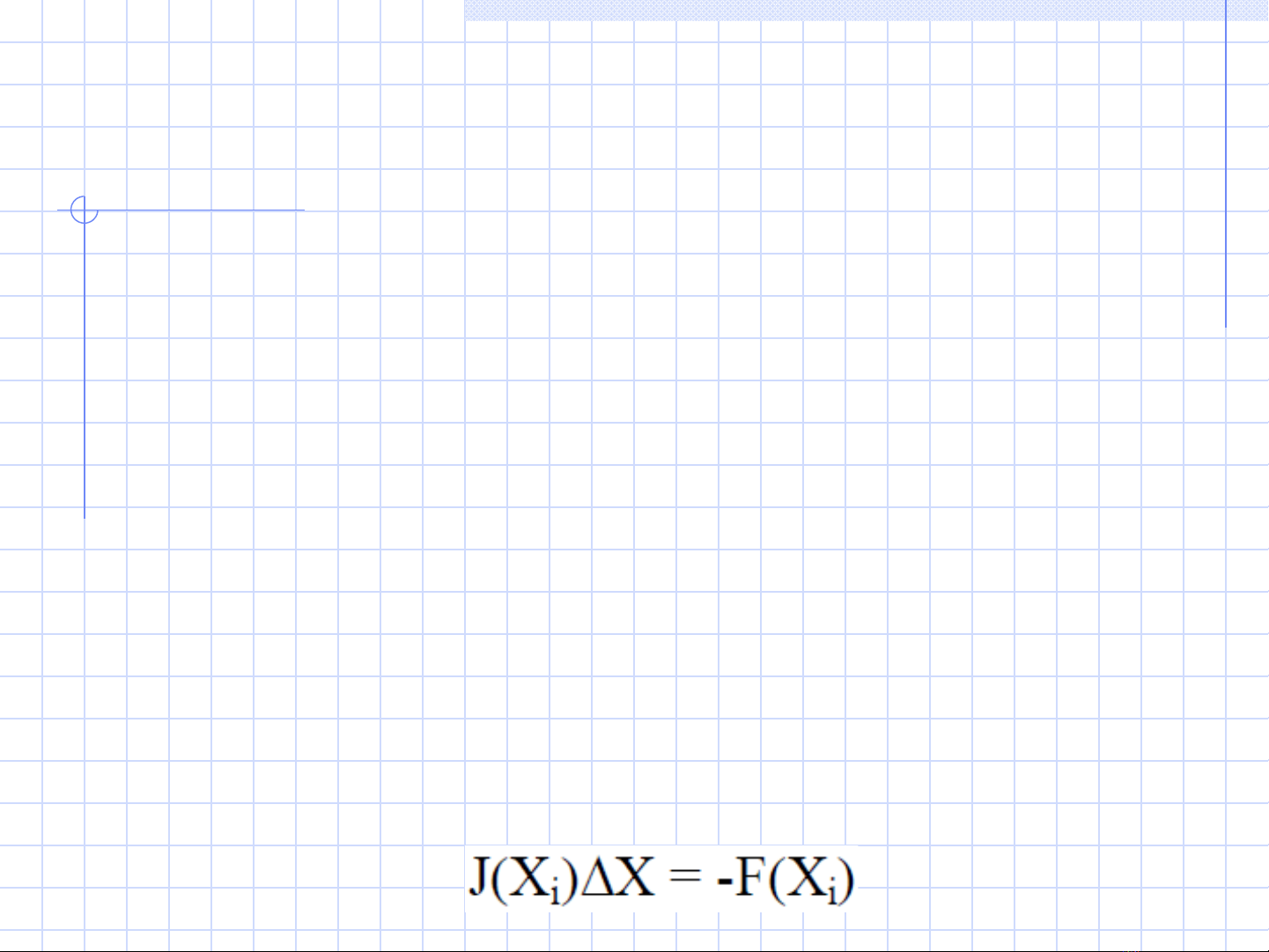
Chương 1. Các phương pháp giải phương
trình và hệ phương trình
1.2 Phương pháp giải phương trình và hệ phương trình
phi tuyến
Gi i h ph ng trình phi tuy n b ng ph ng pháp Newtonả ệ ươ ế ằ ươ
Phương pháp Newton giải hệ phương trình phi tuyến là phương pháp
tuyến tính hóa hệ phương trình đã cho thành một hệ phương trình tuyến
tính mà biến số của hệ là ∆X.
Như vậy ở mỗi bước lặp (bước thứ i), cần phải giải một hệ phương trình
tuyến tính với biến số là ∆Xi cho đến khi được nghiệm gần đúng.
Vì vậy: việc giải hệ phương trình phi tuyến bằng
phương pháp Newton là lặp lại việc giải hệ phương
trình tuyến tính:


























