
S GIÁO D C VÀ ĐÀO T O THANH HÓAỞ Ụ Ạ
TR NG THPT CHUYÊN LAM S NƯỜ Ơ
SÁNG KI N KINH NGHI MẾ Ệ
ĐNG TH NG ĐI SONG ƯỜ Ẳ Ố
Ng i vi t:ườ ế Nguy n Văn Nhi mễ ệ
Ch c v :ứ ụ Giáo viên
SKKN thu c lĩnh v c mônộ ự Toán
1

Thanh Hóa, năm 2016
M C L CỤ Ụ
Trang
1. M đuở ầ 1
2. N i dungộ1
2.1 C s lý lu nơ ở ậ 1
2.2 Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi mự ạ ấ ề ướ ụ ế ệ 3
2.3 Áp d ng ụ4
2.4 Bài t pậ19
3. K t lu n, ki n ngh ế ậ ế ị 21
Tài li u tham kh oệ ả 21
Cam k t c a tác giế ủ ả 21
2
1. M ĐUỞ Ầ
Lí do ch n đ tàiọ ề
Trong các kì thi h c sinh gi i bài toán hình h c ph ng luôn chi m m t v tríọ ỏ ọ ẳ ế ộ ị
trong đ thi, vì v y đ góp ph n nâng cao kĩ năng gi i toán hình h c ph ngề ậ ể ầ ả ọ ẳ
chúng ta c n ph i n m b t đc nh ng ph ng pháp phát hi n v n đ.ầ ả ắ ắ ượ ữ ươ ệ ấ ề
M c đích nghiên c uụ ứ
Trong bài vi t này tôi s gi i thi u phép bi n đi đi song là m t trongế ẽ ớ ệ ế ổ ố ộ
nh ng ph ng pháp đ phát hi n ra t giác n i ti p, quan h song song vàữ ươ ể ệ ứ ộ ế ệ
vuông góc gi a các đng th ng, đng th i cũng là m t ph ng pháp đữ ườ ẳ ồ ờ ộ ươ ể
sáng t o ra nh ng bài toán m i. ạ ữ ớ
Đi t ng nghiên c uố ượ ứ
Thông qua phép bi n đi đi song cung c p thêm m t ph ng pháp t duy,ế ổ ố ấ ộ ươ ư
ti p c n đ gi i quy t các bài toán hình h c ph ng. ế ậ ể ả ế ọ ẳ
Xây d ng m t h th ng bài t p hay và khó đã t ng xu t hi n trong các kìự ộ ệ ố ậ ừ ấ ệ
thi Ôlimpic, đc gi i quy t m i (m t cách s c s o) b ng ph ng pháp phépượ ả ế ớ ộ ắ ả ằ ươ
bi n đi đi song.ế ổ ố
Ph ng pháp nghiên c uươ ứ
Đ tài đc nghiên c u b ng ph ng pháp phân tích, t ng h p.ề ượ ứ ằ ươ ổ ợ
2. N I DUNG Ộ
2.1 C s lý lu nơ ở ậ
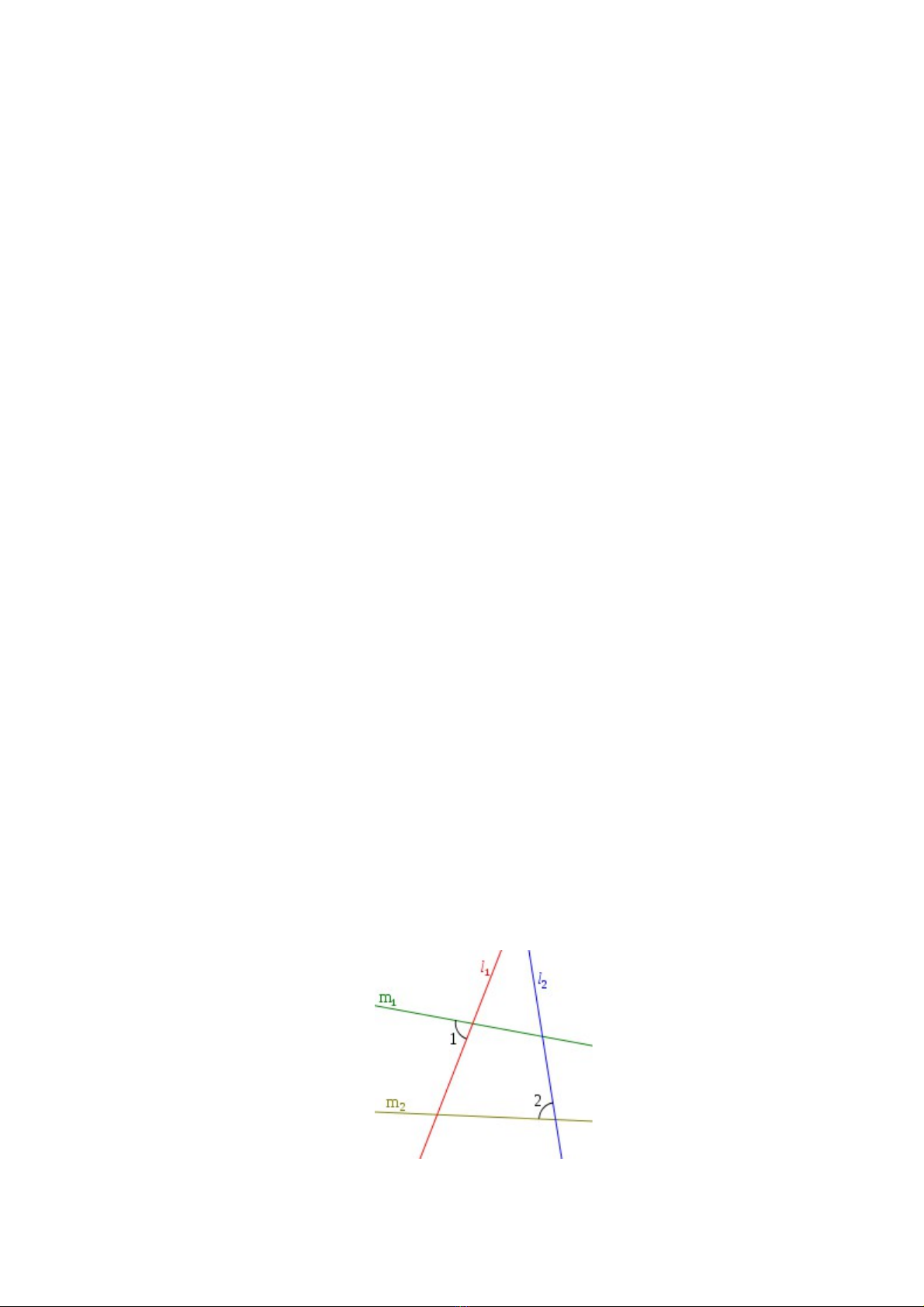
Cho hai đng th ng ườ ẳ
1
m
và
2
m
, hai đng th ng ườ ẳ
1
l
và
2
l
g i là đi song v iọ ố ớ
nhau đi v i hai đng th ng ố ớ ườ ẳ
1
m
và
2
m
, n u nh nh ế ư ả
'
1
l
c a ủ
1
l
qua phép điố
x ng qua đng th ng ứ ườ ẳ m (đng phân giác c a góc t o b i ườ ủ ạ ở
1
m
và
2
m
) là
đng th ng cùng ph ng v i ườ ẳ ươ ớ
2
l
.
3

Nh n xét.ậ N u ta ch đ ý đn hai đng th ng ế ỉ ể ế ườ ẳ
1
l
và
2
l
thì
'
1
l
và
2
l
song song
v i nhau (đây là v n đ hình h c tĩnh). Nh ng phép bi n đi đi song bi n ớ ấ ề ọ ư ế ổ ố ế
m t l p các đng th ng cùng ph ng v i ộ ớ ườ ẳ ươ ớ
1
l
thành m t l p các đng th ng ộ ớ ườ ẳ
cùng ph ng v i ươ ớ
2
l
(m i đng th ng trong l p ỗ ườ ẳ ớ
1
l
đu đi song v i m t ề ố ớ ộ
đng th ng trong l p ườ ẳ ớ
2
l
) (đây là v n đ hình h c đng).ấ ề ọ ộ
Ta có m t s m i liên h sau đây v đng th ng đi song trong tamộ ố ố ệ ề ườ ẳ ố
giác
Cho tam giác ABC, hai đi m P, Q l n l t thu c hai đng th ng AB, AB.ể ầ ượ ộ ườ ẳ
N u đng th ng PQ đi song v i BC đi v i hai đng th ng ch a haiế ườ ẳ ố ớ ố ớ ườ ẳ ứ
c nh AB, AC, thì ta còn nói PQ đi song v i BC đi v i đnh A trong tam giácạ ố ớ ố ớ ỉ
ABC, hay còn nói QP đi song v i BC trong tam giác ABC.ố ớ
a) Trong m t tam giác đng th ng n i chân hai đng cao là đng điộ ườ ẳ ố ườ ườ ố
song v i đng th ng ch a c nh còn l i.ớ ườ ẳ ứ ạ ạ
b) Ti p tuy n t i m i đnh c a đng tròn ngo i ti p tam giác là đng điế ế ạ ỗ ỉ ủ ườ ạ ế ườ ố
song c a đng th ng ch a c nh đi di n đnh đó.ủ ườ ẳ ứ ạ ố ệ ỉ
c) Bán kính đi qua m i đnh c a tam giác vuông góc v i đng đi song c aỗ ỉ ủ ớ ườ ố ủ
c nh đi di n đnh đó.ạ ố ệ ỉ
d) Cho tam giác ABC, đng tròn đi qua hai đnh B, C c t hai đng th ngườ ỉ ắ ườ ẳ
AB, AC t i hai đi m P, Q. Khi đó đng kính đi qua đnh A c a đng trònạ ể ườ ỉ ủ ườ
ngo i ti p tam giác ABC vuông góc v i PQ và đng kính đi qua đnh A c aạ ế ớ ườ ỉ ủ
đng tròn ngo i ti p tam giác APQ vuông góc v i BC.ườ ạ ế ớ
e) Trong m t tam giác đng cao và đng kính c a đng tròn ngo i ti pộ ườ ườ ủ ườ ạ ế
tam giác cùng đi qua m t đnh thì đi song v i nhau đi v i hai c nh đi quaộ ỉ ố ớ ố ớ ạ
đnh đó.ỉ
f)Trong tam giác đng đi trung và đng trung tuy n cùng đi qua m t đnhườ ố ườ ế ộ ỉ
thì đi song v i nhau, đi v i hai c nh đi qua đnh đó.ố ớ ố ớ ạ ỉ
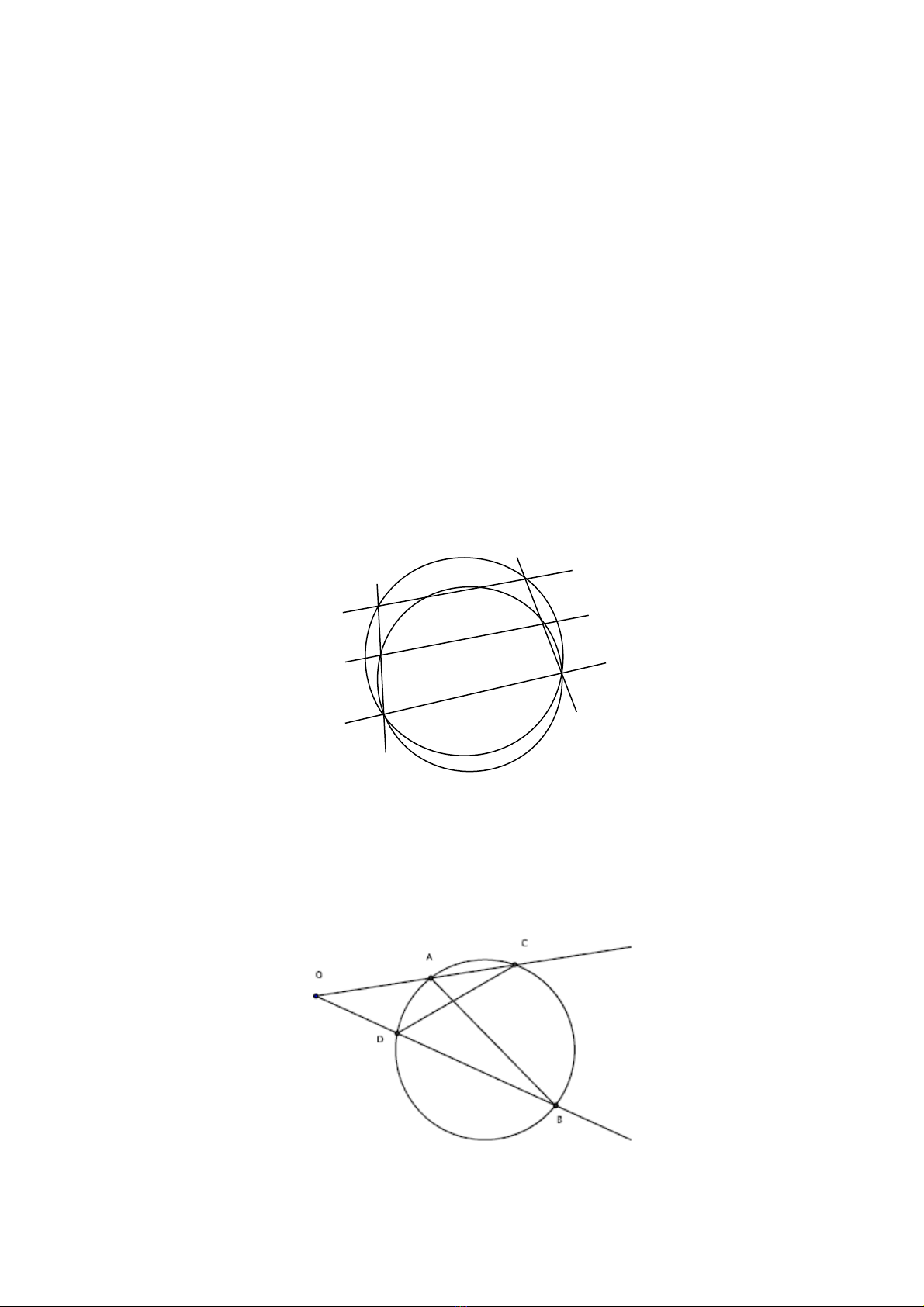
H qu :ệ ả Đng tròn đi qua hai đi m B, C c t hai đng th ng AB, AC t iườ ể ắ ườ ẳ ạ
hai đi m B’, C’. Khi đó đng th ng n i A v i giao đi m c a hai ti p tuy nể ườ ẳ ố ớ ể ủ ế ế
t i B’, C’ c a đng tròn ngo i ti p tam giác AB’C’ đi qua trung đi m BCạ ủ ườ ạ ế ể .
4
A
B’
B
C
C’
N
T
M
g) Trong m t tam giác hai đng đi song cùng đi qua m t đnh thì đng giácộ ườ ố ộ ỉ ẳ
v i nhau. Nh v y hai đng đng giác là tr ng h p đc bi t c a haiớ ư ậ ườ ẳ ườ ợ ặ ệ ủ
đng đi song.ườ ố
Ta có m i liên h sau đây v đng th ng đi song trong t giác n iố ệ ề ườ ẳ ố ứ ộ
ti pế
Trong m t t giác n i ti p đng tròn, c p c nh đi di n đi song v i nhauộ ứ ộ ế ườ ặ ạ ố ệ ố ớ
đi v i c p c nh còn l i.ố ớ ặ ạ ạ
Nh v y, n u t giác ABCD n i ti p đng tròn và đng tròn ư ậ ế ứ ộ ế ườ ườ
ω
thay đi điổ
qua hai đnh C, D c t các đng th ng AD, BC l n l t t i M, N thì MN//AB.ỉ ắ ườ ẳ ầ ượ ạ
Ta th ng s d ng đi u ki n đi song d i d ng sau:ườ ử ụ ề ệ ố ướ ạ
Cho A, C thu c Ox và B, D thu c Oy ộ ộ
( , , , )A B C D O
. Khi đó AB đi song v iố ớ
CD khi và ch khi t giác ACBD n i ti p.ỉ ứ ộ ế
5
N
A
B
C
D
M
ω


























