PHM NGC TUÂN – CĐT3.K52
Thuyết minh cảm biến đo lường-xử kí tín hiệu đo
A.LÍ THUYẾT BIẾN ĐỔI FOURIE NHANH (FFT)
1.
Biến đổi Fourier nhanh (FFT
–
Fas Fourier
Transform)
1.1,Tính toán DFT trực tiếp
Từ công thức định nghĩa DFT, ta có:
1
0
2 2
c o s . s i n
N
n
k n k n
X n x n j
N N
Nếu x(n) là tín hiệu thực:
1
0
2
c o s
N
Rn
k n
X k x n N
1
0
2
. s i n
N
In
k n
X k x n j N
2 2
| | ( ) ( )
R I
X k X k X k
( )
K
X
k arctg
X
Nếu x(n) là tín hiệu phức, các thành phần thực và ảo tính toán theo công thức
1
0
2 2
c . o s . s i n
N
R I K
n
k n k n
X k x n x n
N N
1
0
2 2
c . o s . s i n
N
I I K
n
k n k n
X k x n x n
N N
Để thực hiện tính toán theo công thức này, đòi hỏi các phép toán sau:
-
2N2
hàm lượng giác,
4N2
phép nhân số thực, 4N(N –
1) phép cộng số
thực
1.2.Thuật toán FFT cơ số 2
1.2.1
.
Trên miền thời gian
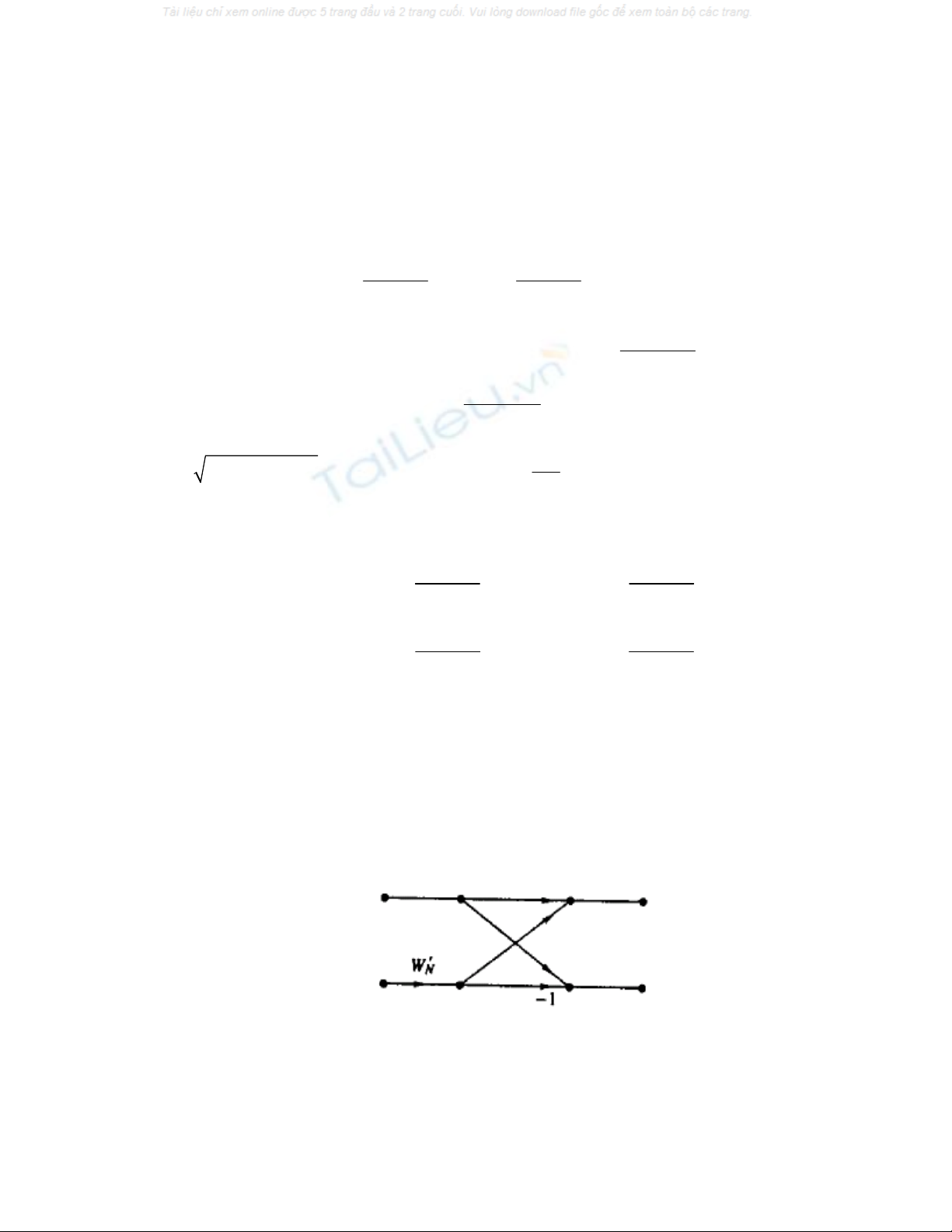
Thuật toán thực hiện DFT trên được xây dựng dựa cơ sở theo sơ đồ hình
bướm
A = a + W'Nb
sau: b
B = a - W'Nb
Tính toán cho sơ đồ hình bướm cơ sở của thuật toán FFT
1.2.2
.
Trên miền tần số
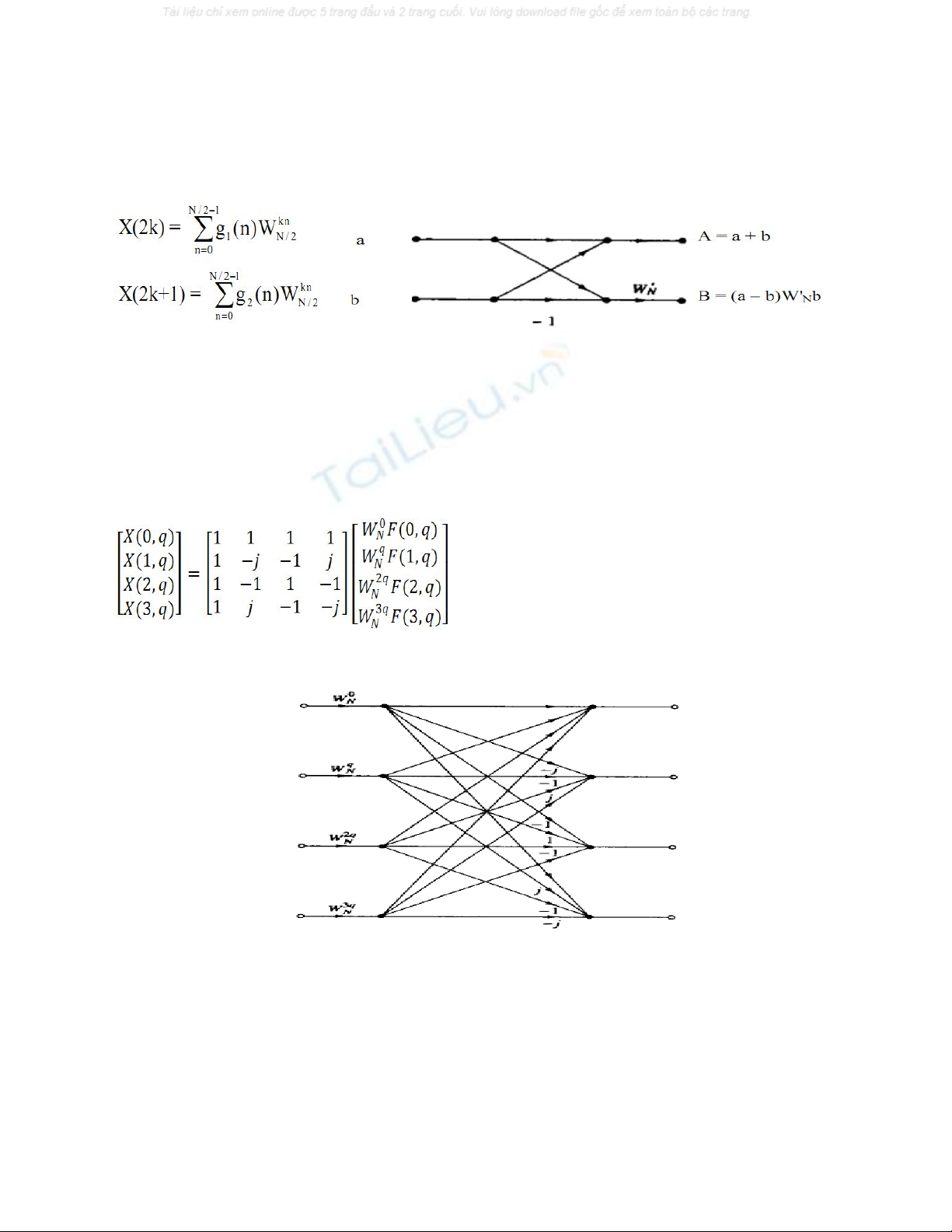
Xét DFT N điểm:
a
PHM NGC TUÂN – CĐT3.K52
Ta định nghĩa hai chuỗi N/2 điểm g
1(n) và g2
(n) như sau:
1
g n x n x n N / 2
;
2
g n x n -x n N / 2 .
n
N
W
Khi đó:
Tính toán cho sơ đồ hình bướm cơ sở của thuật toán FFT trên miền tần số
1. 3. Thuật toán FFT cơ số 4
1.3.1
.
Trên miền thời gian
Xét DFT N điểm có N là lũy thừa của 4 (N = 4
v).quá trình thực hiện DFT N điểm có thể
thông qua thực hiện 4 DFT N/4
điểm
.
Biểu thức thực hiện mô tả như sau
Sơ đồ mô tả quá trình thực hiện:
Tính toán cho sơ đồ hình bướm cơ sở của thuật toán FFT cơ số 4
1.3.2
.
Trên miền tần số( Tương tự như FFT cơ số 2)
2.
Tính toán FFT dùng xấp xỉ lọc tuyến tính
PHM NGC TUÂN – CĐT3.K52
2.1 Thuật toán Goertzel
Thuật toán Goertzel thực hiện dựa trên khai triển tuần hoàn hệ số pha
W
k
n
.
Do
W 1
kN
n
nên
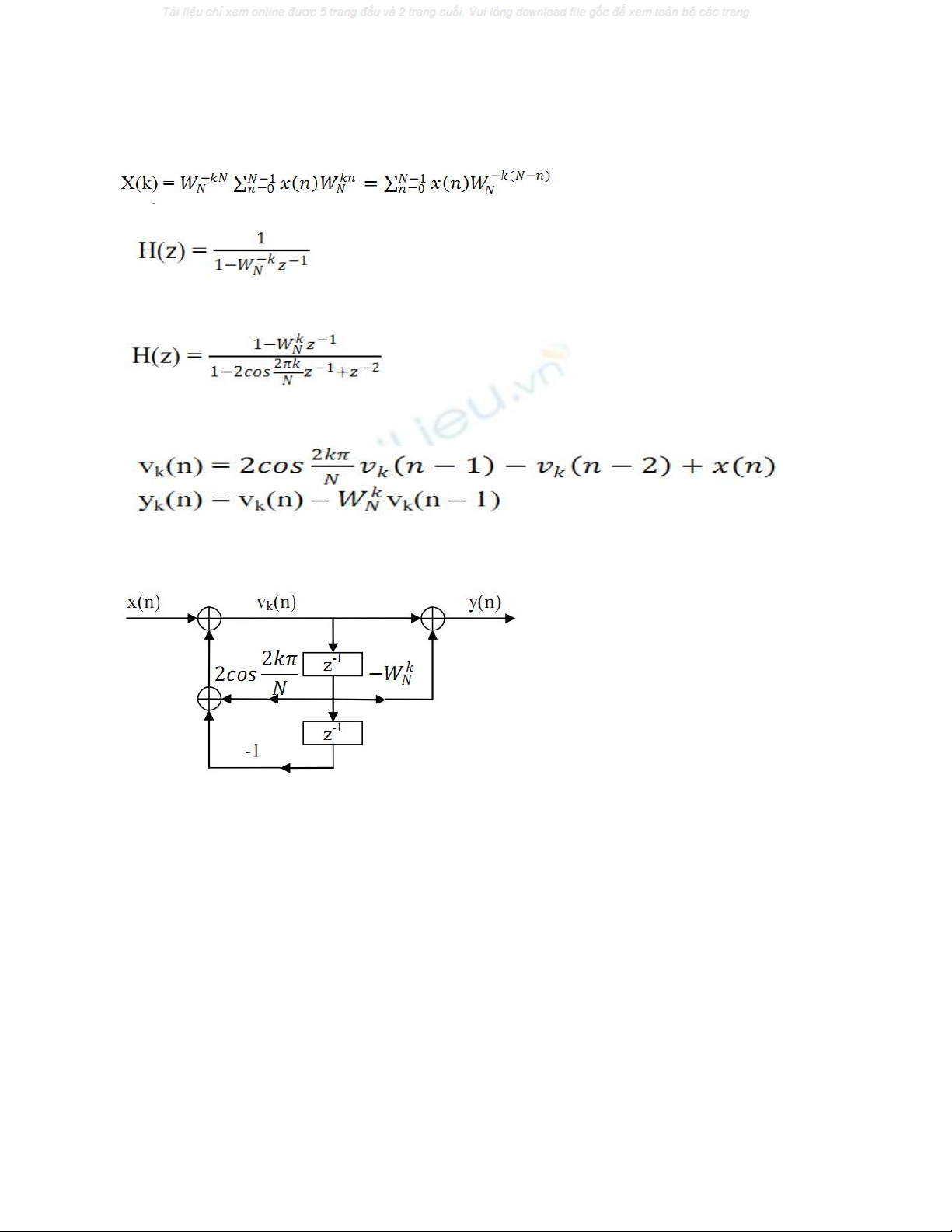
Mạch lọc với đáp ứng xung h(n) có hàm hệ thống là
Hàm hệ thống của phương trình sai phân là
Dạng trực tiếp loại 2 của hệ thống mô tả bằng phương trình sai phân sau
với điều kiện đầu v
k(-1) = vk(-2) = 0.
2.2 Thuật toán Chirp-z
Xác định tổng chập vòng của chuỗi g(n) N điểm và chuỗi h(n) M điểm (M > N)
–
N-1 điểm
đầ
u là các đi
ể
m lặp lại
–
M-(N-1) điểm còn lại ch
ứ
a kết quả
N
-
1
y(k)
=
g(n)h(k
-
n
)
k = 0,1,K, L
-
1
n=
0
Gi
ả s
ử
M = L + (N-1)
M
đ
iểm của chuỗi h(n)
đượ
c xác định –(N–1) ≤ n ≤
(L–1)
1
-
=
PHM NGC TUÂN – CĐT3.K52
Định nghĩa chuỗi M
đ
iểm h1(n) = h(n–N+1) n = 0,1,…,M–1
H1(k) = DFTM{h1(n)}
G(k) = DFTM{g(n)} (sau khi
đ
ã
đệ
m thêm vào g(n) L-1 s
ố
0)
Y1(k) = G(k)H(k) → y1(n) = IDFT{Y1(k)} n = 0,1,…,M–1
N-1 điểm
đầ
u tiên của y1(n) là các điểm lặp → loại bỏ
chúng
Các điểm kết quả là giá trị của y1(n) khi N-1 ≤ n ≤
M–1
–
y(n) = y1(n+N-1) n = 0,1,…,L-1
X(zk)= y(k)/h(k) k = 0,1,…,L-1
B.Baì tập
9.2.1
a.Tính DFT bằng thuật toán cơ số 2 phân chia theo thời gian
>> x=[3 2 1 0;2.5 1.5 0.5 0]
x =
3.0000 2.0000 1.0000 0
2.5000 1.5000 0.5000 0
>> xfft=fft(x)
xfft =
5.5000 3.5000 1.5000 0
0.5000 0.5000 0.5000 0
b. Tính DFT bằng thuật toán cơ số 4 phân chia theo thời gian
PHM NGC TUÂN – CĐT3.K52
>> x=[3 1 0 0;2.5 0.5 0 0;2 0 0 0;1.5 0 0 0]
x =
3.0000 1.0000 0 0
2.5000 0.5000 0 0
2.0000 0 0 0
1.5000 0 0 0
>> xfft=fft(x)
xfft =
9.0000 1.5000 0 0
1.0000 - 1.0000i 1.0000 - 0.5000i 0 0
1.0000 0.5000 0 0
1.0000 + 1.0000i 1.0000 + 0.5000i 0 0
>>
9.2.2 Tính DFT bằng thuật toán cơ số 2 phân chia theo miền tần số
>> x=[0.5 0.5 0.5 0.5;0 0 0 0]
x =