BÀI TẬP LỚN CẢM BIẾN
Đề tài Số 3 : Tín hiệu & Hệ thống trong miền tần số
Sinh viên : Đào văn Hân
Lớp : Cơ điện tử 4 K52
SHSV : 20071052
Nội Dung:
1. Tóm tắt lý thuyết
2. Trình bày một số câu lệnh của Matlab sử dụng trong tín hiệu số
3. Trình bày một số ví dụ về tín hiệu và hệ thống trong miền tần số
Tín hiệu & Hệ thống trong miền tần số
+ Tần số của tín hiệu liên tục thời gian tuần hoàn
+ Tần số của tín hiệu liên tục thời gian không tuần hoàn
+ Tần số của tín hiệu rời rạc thời gian tuần hoàn
+ Tần số của tín hiệu rời rạc thời gian không tuần hoàn
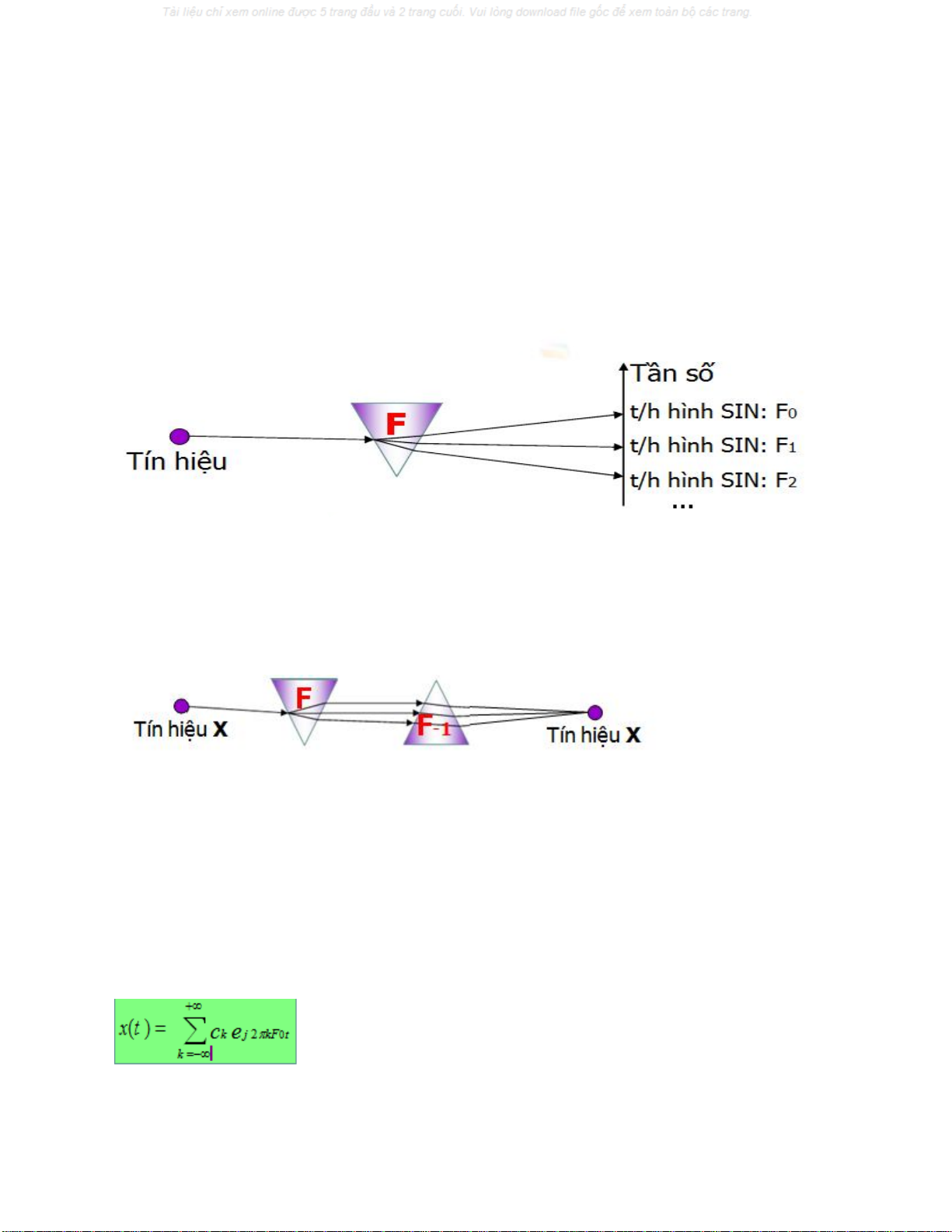
Tại sao miền tần số ?
F: Công cụ phân tích tần số
- Chuỗi Fourier – tín hiệu tuần hoàn
- Biến đổi Fourier – tín hiệu năng lượng, không tuần hoàn
(J.B.J. Fourier: 1768 - 1830)
F-1 Công cụ tổng hợp tần số
- Chuỗi Fourier ngược – tín hiệu tuần hoàn
- Biến đổi Fourier ngược – tín hiệu năng lượng, không tuần hoàn
1. Tín hiệu liên tục thời gian và tuần hoàn
+ x(t): LTTG, tuần hoàn với chu kỳ cơ bản Tp = 1/F0 (F0: tần số)
phương trình tổng hợp
phương trình phân tích
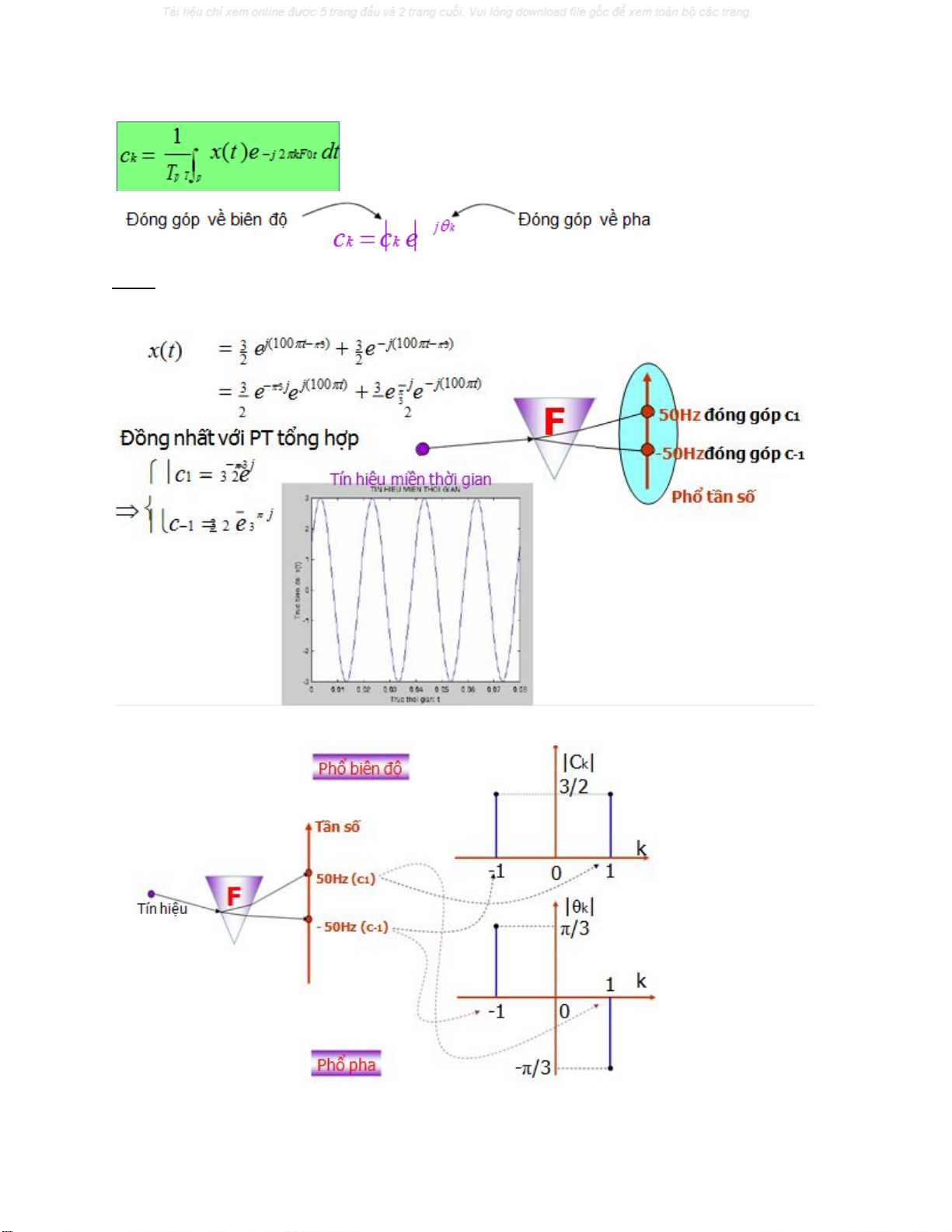
Ví dụ: Phân tích tín hiệu sau ra các thành phần tần số
x(t) = 3Cos(100πt – π/3)
2. Tín hiệu thời gian liên tục không tuần hoàn
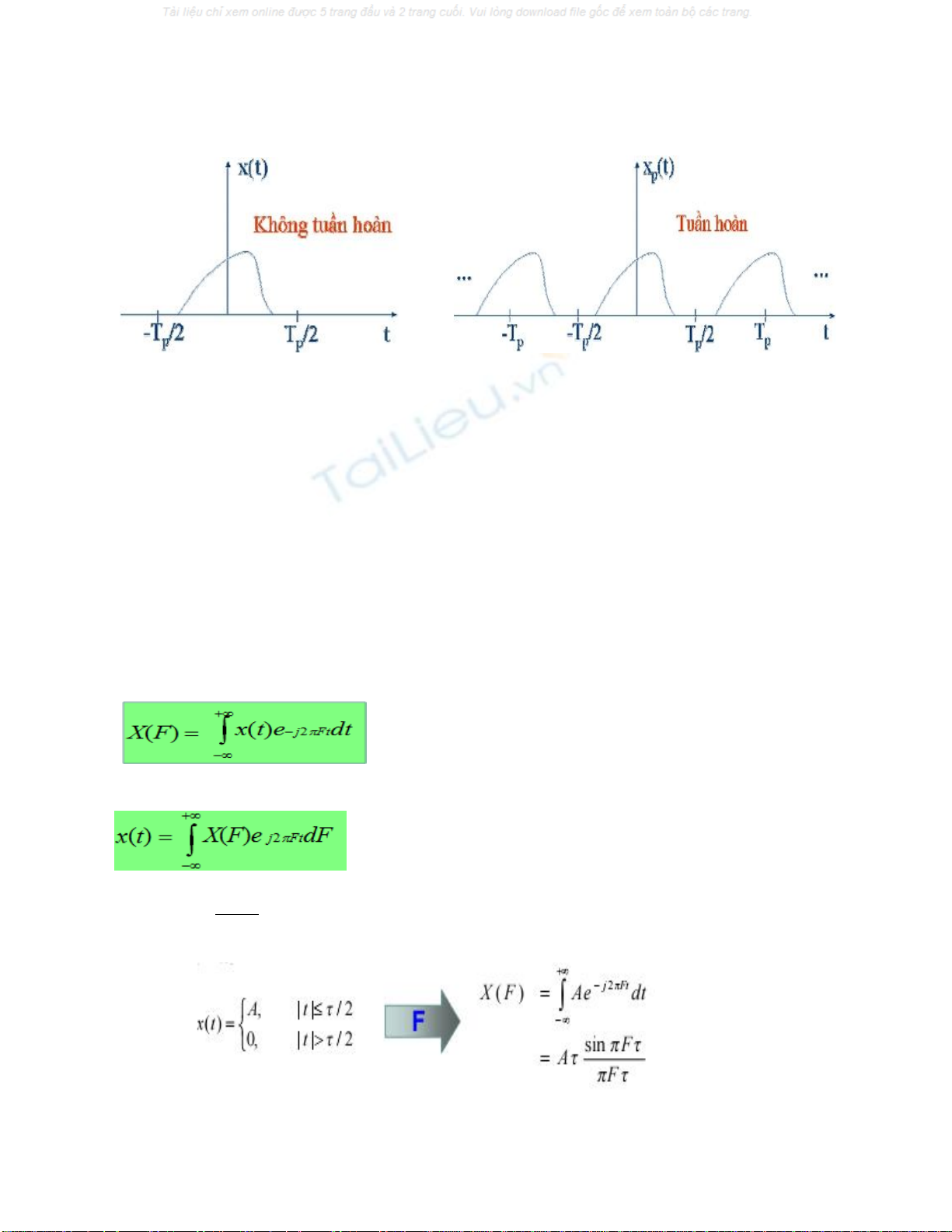
T/h tuần hoàn xp(t)
Có được do lặp lại t/h x(t), Tuần hoàn chu kỳ cơ bản Tp, Có phổ vạch: khoảng cách
vạch F0=1/Tp
T/h không tuần hoàn x(t)
Có thể coi như xp(t) khi Tp → ∞ Khoảng cách vạch F0 = 1/Tp → 0
Phổ của tín hiệu không tuần hoàn là ph
ổ
liên t
ụ
c
x(t): LTTG, không tuần hoàn
Phương trình phân tích(biến đổi Fourier thuận)
Phương trình tổng hợp(biến đổi Fourier ngược)
Ví dụ: Ví dụ: cho x(t) không tuần hoàn. Phân tích x(t) ra các thành
phần tần số
3. Tần số của tín hiệu rời rạc thời gian tuần hoàn
+ x(n) là t/h tuần hoàn chu kỳ N x(n+N) = x(n) mọi n
+ Chuỗi Fourier cho t/h RRTG có tối đa N thành phần tần số (do tầm tần
số [0, 2π] hoặc [-π, π])
+ Chuỗi Fourier rời rạc (DTFS)
phương trình tổng hợp phương trình phân tích
Mô tả x(n) trong miền tần số (ck biểu diễn biên độ và pha của thành phần tần số sk(n) =
ej2πkn/N)
ck+N = ck → Phổ của t/h tuần hoàn x(n) với chu kỳ N là một chuỗi tuần hoàn
cũng với chu kỳ N
Ví dụ: Xác định và vẽ phổ cho t/h sau x(n) = 3cos( √2n)