
H Th C m Hoài, PhDồ ị ẩ 1
TR NG THÁI KHÍẠ
TR NG THÁI KHÍẠ
Hoá Đ i C ng A1ạ ươ
Hoá Đ i C ng A1ạ ươ

H Th C m Hoài, PhDồ ị ẩ 2
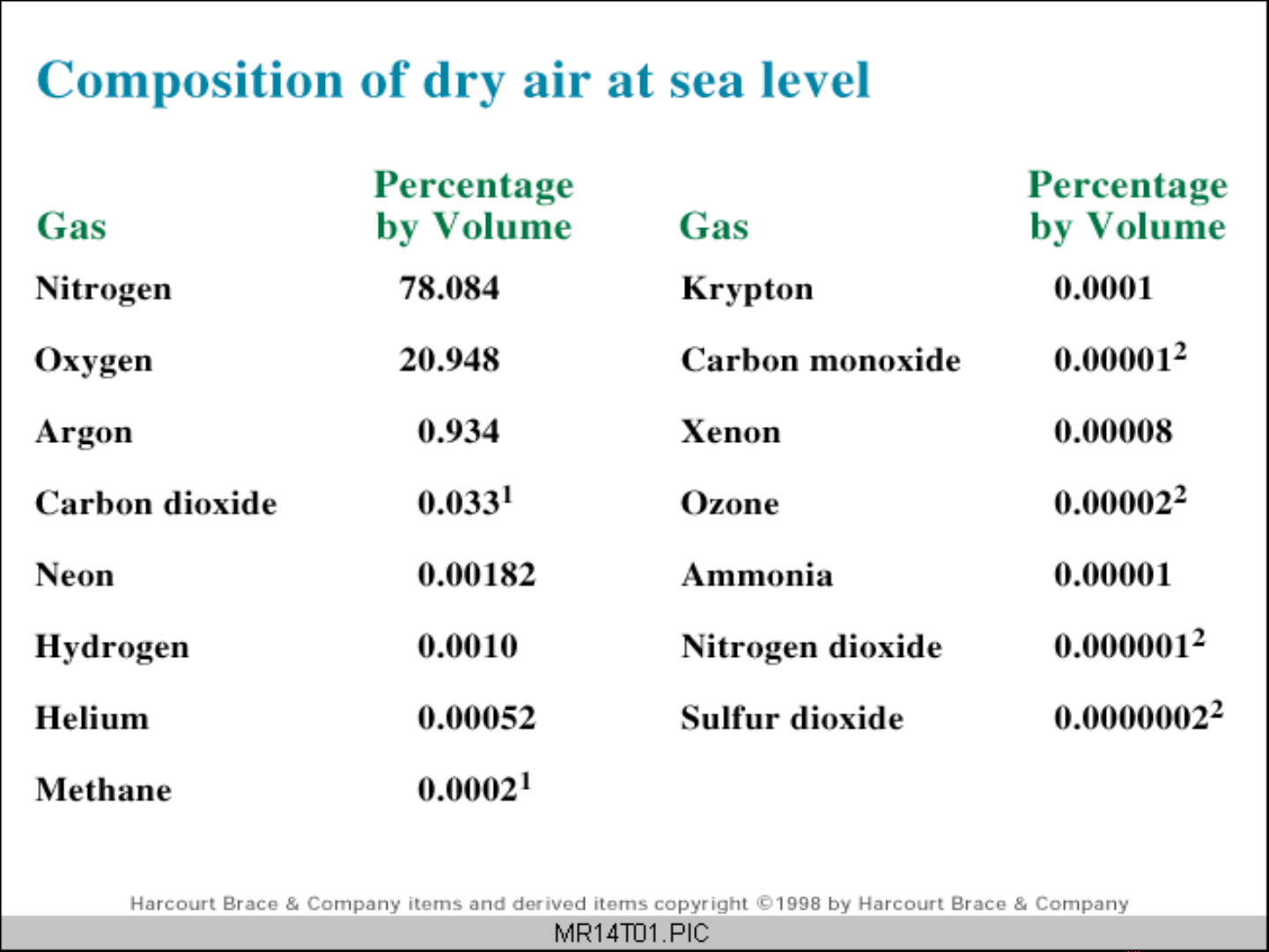
Các tính ch t c a khíấ ủ
Các tính ch t c a khíấ ủ
•M i v t ch t t n t i 3 pha: r n, l ng và ọ ậ ấ ồ ạ ở ắ ỏ
khí.
•Các ch t khí d b nén, ép và phân b ấ ễ ị ố
trong toàn b th tích v t ch a chúng.ộ ể ậ ứ
•Khi m t ch t khí b nén, th tích c a nó ộ ấ ị ể ủ
gi m.ả
•Các ch t khí luôn luôn t o h n h p đ ng ấ ạ ỗ ợ ồ
th v i các ch t khí khác.ể ớ ấ
H Th C m Hoài, PhDồ ị ẩ 3
H Th C m Hoài, PhDồ ị ẩ 4

H Th C m Hoài, PhDồ ị ẩ 5
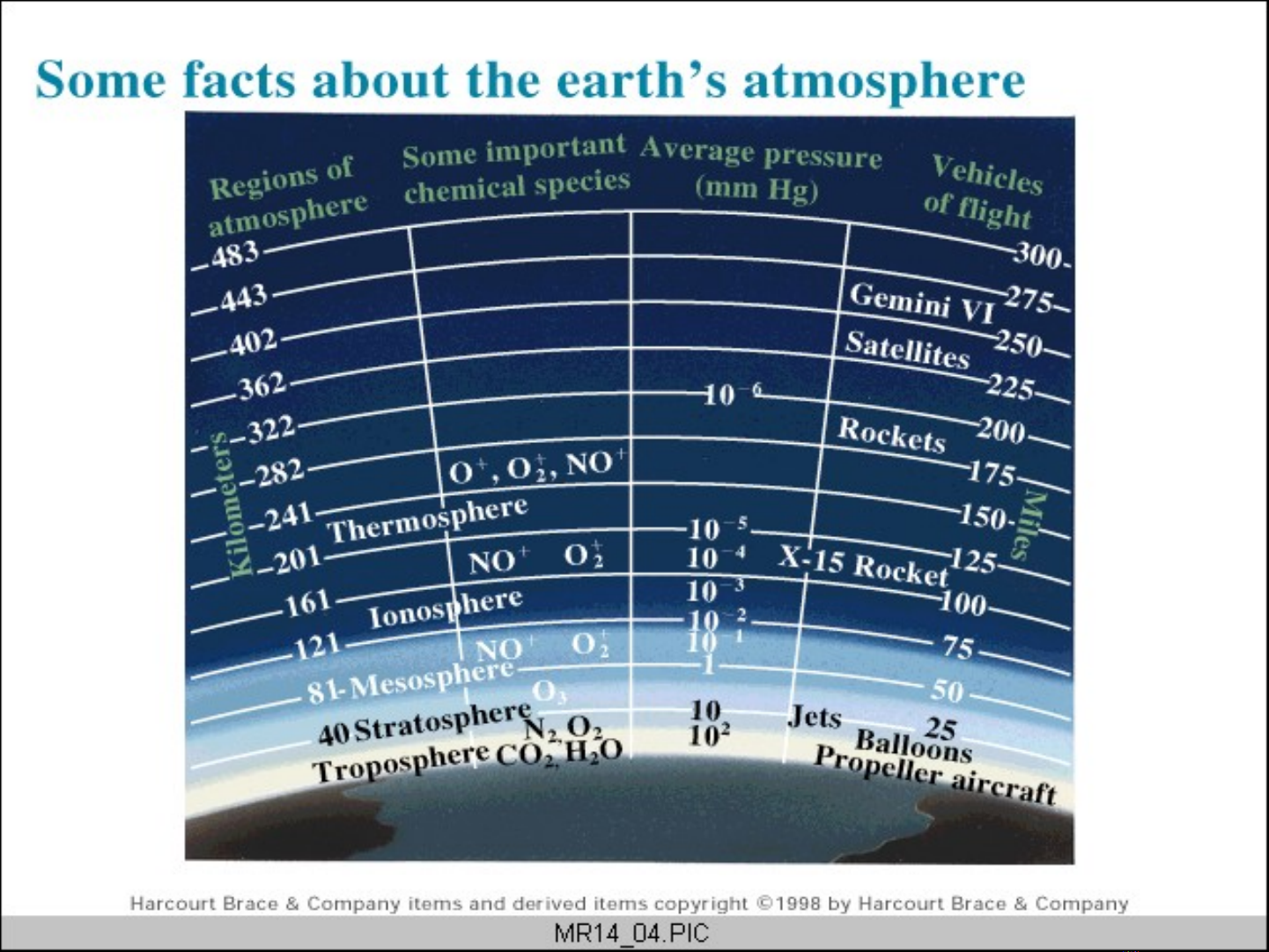
ÁP SU TẤ
ÁP SU TẤ
Áp su t không khí và khí áp k (barometer)ấ ế
Áp su t không khí và khí áp k (barometer)ấ ế
•Áp su t là l c tác d ng trên m t đ n v di n ấ ự ụ ộ ơ ị ệ
tích:
•Tr ng l c t o nên m t l c lên khí quy n c a trái ọ ự ạ ộ ự ể ủ
đ t. ấ
•M t c t không khí ti t di n ộ ộ ế ệ 1 m2 t o nên m t l c ạ ộ ự
là 105 N.
•Áp su t c a c t không khí ấ ủ ộ 1 m2 là 100 kPa.
A
F
P
=


























