14
Chương 1
DAO ĐỘNG TUYẾN TÍNH CỦA HỆMỘT BẬC TỰDO
1.1. Dao động tựdo không cản.
1.2. Dao động tựdo có cản.
1.3. Dao động cưỡng bứccủahệchịukíchđộng điều
hòa.
1.4. Dao động cưỡng bứccủahệchịukíchđộng đa
tầnvàchịukíchđộng tuầnhoàn.
1.5. Dao động cưỡng bứccủahệchịukíchđộng bất
kỳ.
15
§1. Dao động tựdo không cản
1.1. Mộtsốví dụ.
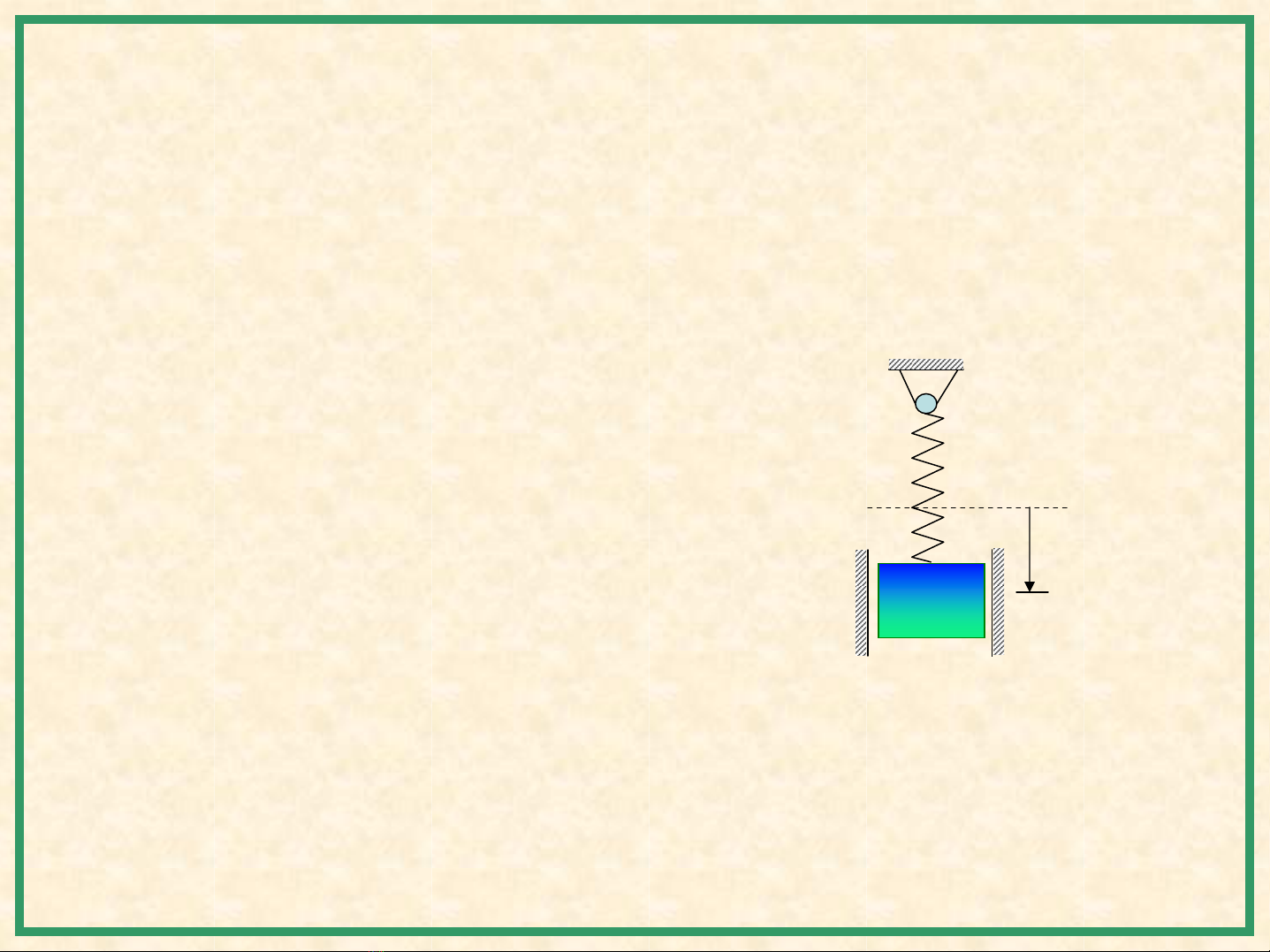
Thí dụ1: Dao động củamộtvậtnặng treo vào lò xo.
m
c
x
Vịtrí cb tĩnh
0mx cx+=
&&
Æ Phương trình dao động:
(1)
16
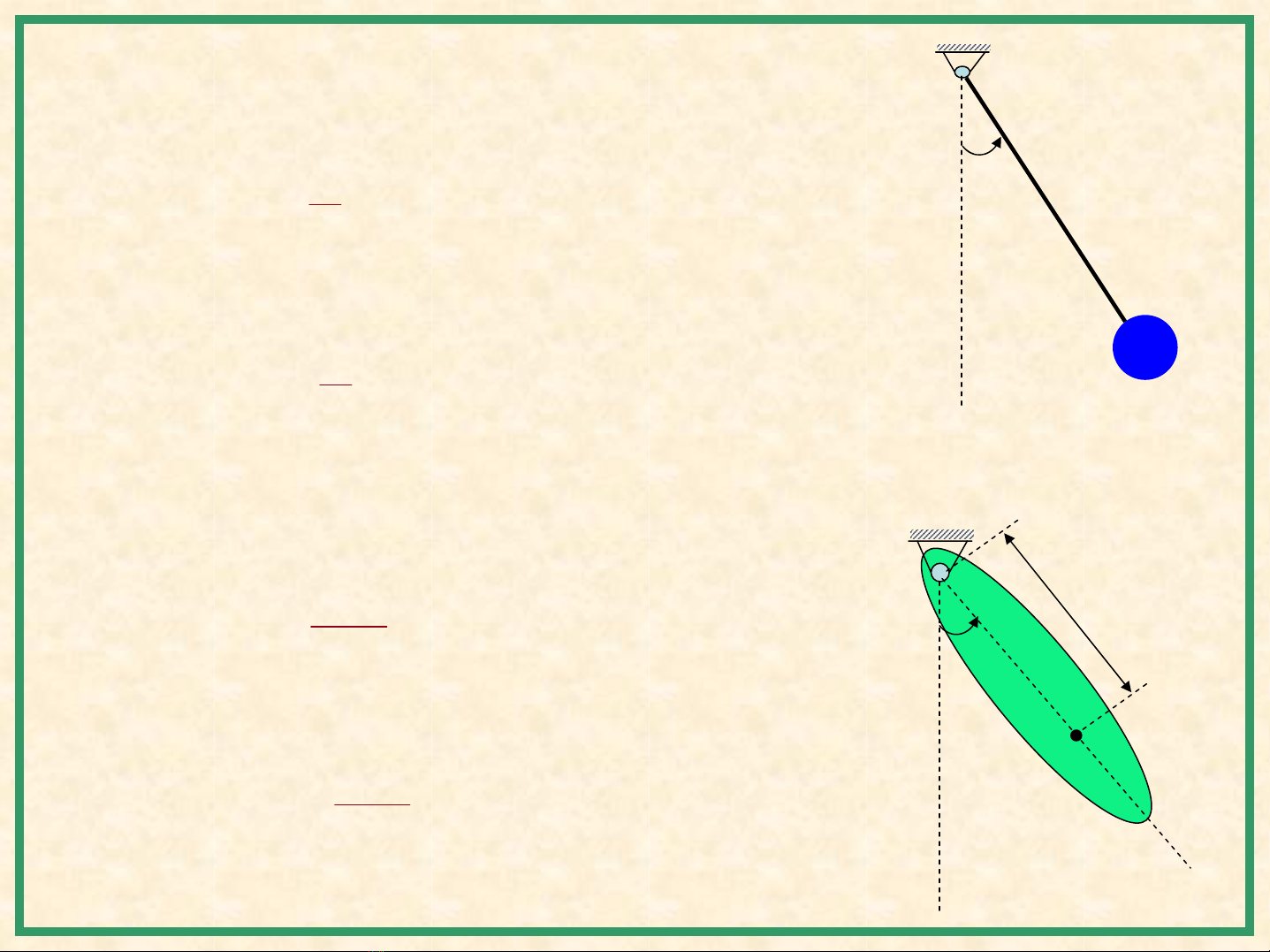
Thí dụ2: Dao động củacon lắctoánhọc. O
L
m
φ
Æ Phương trình dao động:
sin 0
g
l
ϕ
ϕ
+=&&
Xét dao động nhỏ:
0
g
l
ϕ
ϕ
+=&& (2)
Thí dụ3: Dao động củacon lắcvậtlý.
O
m, Jo
φ
C
a
Æ Phương trình dao động:
sin 0
o
mga
J
ϕϕ
+=
&&
Xét dao động nhỏ:
(3)
0
o
mga
J
ϕϕ
+=
&&
17
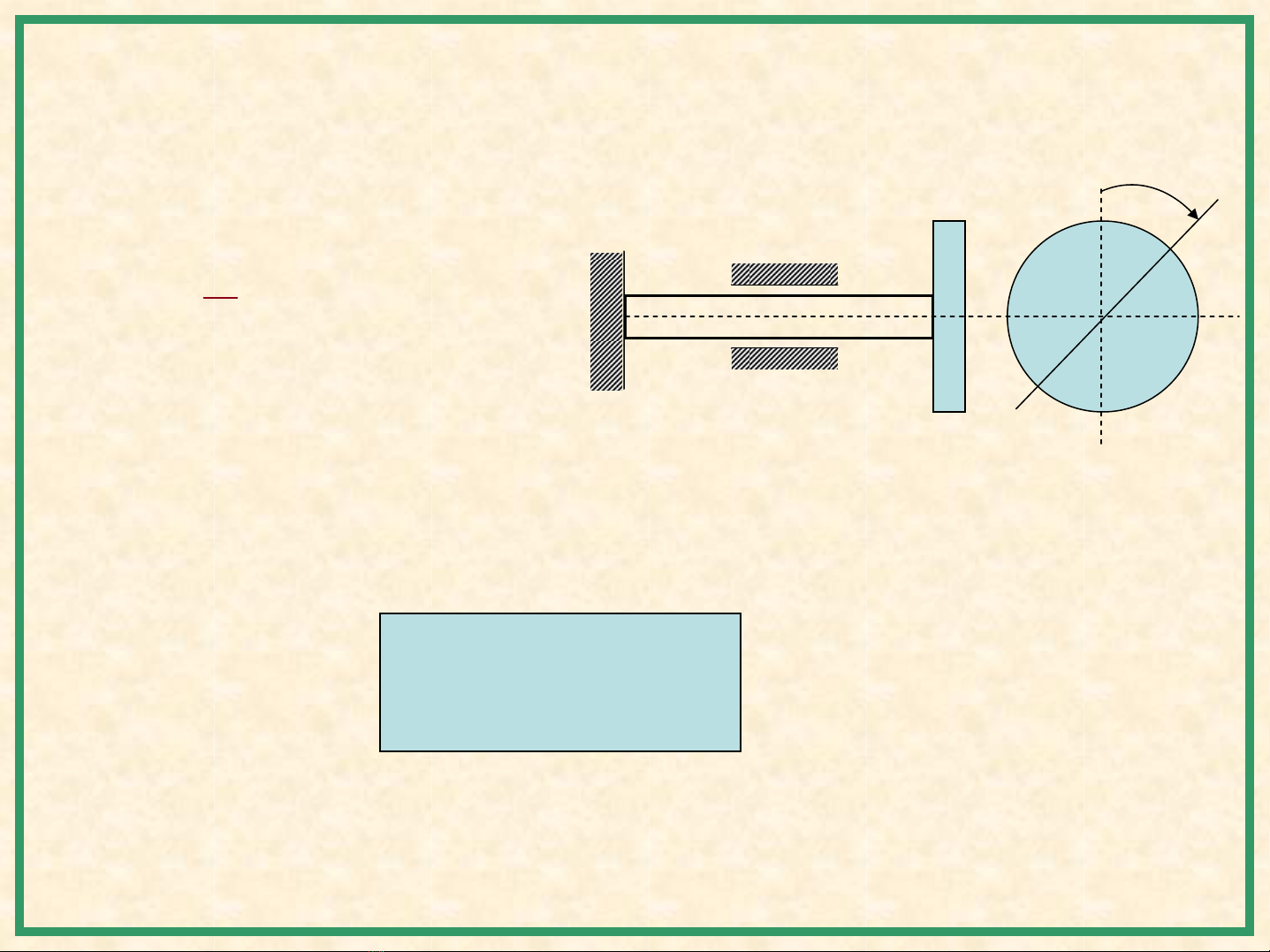
Thí dụ4: Dao động xoắncủatrục mang đĩa tròn.
C
φ
J
Æ Phương trình dao động:
0
c
J
ϕϕ
+=
&& (4)
Kếtluận: Dạng của phương trình dao động tựdo củahệ
mộtbậctựdo có dạng chung là:
0mq cq
+
=
&& (5)
Trong đóq làtọađộ suy rộng.
18
1.2. Tính toán dao động tựdo không cản.
Phương trình vi phân chuyểnđộng củacơhệmộtbậc
tựdo không cảncódạng:
20
o
qq
ω
+
=
&& (6)
Trong đóωolà tần sốdao động riêng.
Điềukiệnđầu: to= 0 : 0
() o
qt q=
0
() o
qt q=
&&
(7)
0mq cq
+
=
&&
Hay: