ĐỀ TÀI
“ỨNG DỤNG LIÊN HỆ GIỮA
DAO ĐỘNG ĐIỀU HÒA VÀ
CHUYỂN ĐỘNG
TRÒN ĐỀU ĐỂ GIẢI CÁC BÀI
TOÁN TRONG CHƯƠNG DAO
ĐỘNG CƠ”
Sáng kiến kinh nghiệm Bùi Thị Thắm-THPT Nguyễn Viết Xuân
1
MỞ ĐẦU
A. ĐẶT VẤN ĐỀ Trang
I. Thực trạng của vấn đề.......................................................................... 2
II. Nhiệm vụ và phương pháp nghiên cứu .............................................. 2
III. Phạm vi của đề tài.............................................................................. 2
B. NỘI DUNG
I.Cơ sở lí thuyết ........................................................................................ 3
I.1.Liên hệ giữa dao động điều hòa và chuyển động tròn đều ............... 3
I.2.Cách xác định vị trí ban đầu của chất điểm…………………………4
II.ỨNG DỤNG GIẢI CÁC BÀI TẬP CHƯƠNG DAO ĐỘNG CƠ
II.1. Dạng toán xác định các đại lượng,viết phương trình dao động……6
II.2. Dạng toán xác định thời điểm, thời gian……………………………8
II.3.Dạng toán xác tìm vị trí, khoảng cách, quãng đường vật đi được…..14
II.4.Dạng toán hai vật dao động…………………………………………17
II.5.Bài tập đề nghị………………………………………………………20
C.KẾT LUẬN................................................................................………25
Sáng kiến kinh nghiệm Bùi Thị Thắm-THPT Nguyễn Viết Xuân
2
“ ỨNG DỤNG LIÊN HỆ GIỮA DAO ĐỘNG ĐIỀU HÒA VÀ CHUYỂN ĐỘNG
TRÒN ĐỀU ĐỂ GIẢI CÁC BÀI TOÁN TRONG CHƯƠNG DAO ĐỘNG CƠ”
A
A.
.
Đ
ĐẶ
ẶT
T
V
VẤ
ẤN
N
Đ
ĐỀ
Ề
I
I.
.
L
Lí
í
d
do
o
c
ch
họ
ọn
n
đ
đề
ề
t
tà
ài
i
Trong những năm gần đây Bộ GD-ĐT đã áp dụng hình thức thi trắc nghiệm khách quan
trong kì thi tốt nghiệp THPT cũng như tuyển sinh đại học, cao đẳng đối với nhiều môn
học trong đó có mộn vật lý. Hình thức thi trắc nghiệm khách quan đòi hỏi học sinh phải
có kiến thức rộng, xuyên suốt chương trình và có kĩ năng làm bài, trả lời câu trắc
nghiệm nhanh chóng. Bởi vậy,với mỗi bài toán đề ra, người giáo viên không chỉ hướng
dẫn học sinh hiểu bài mà phải tìm cách giải nhanh nhất có thể.
Việc sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều để giải
các bài tập dao động đã thỏa mãn được điều đó. Tuy nhiên, không phải học sinh nào
cũng nắm được thuần thục và nhanh nhạy công cụ này do các em rất lúng túng khi dùng
đường tròn lượng giác và khó tưởng tượng được sự tương tự giữa hai loại chuyển động
này. Trên thực tế, đã có khá nhiều đề tài nghiên cứu xung quanh vấn đề này và đã thu
được một số kết quả nhất định. Tuy nhiên, các tác giả chưa hoặc còn ít khái quát lại vấn
đề, tổng hợp thành cách nhớ nhanh, rất ít hoặc chưa đề cập đến bài toán có nhiều vật dao
động .Để giúp các em dễ dàng hơn khi tiếp cận, có cái nhìn tổng quát và có cơ sở để giải
quyết các bài tập chương sau, tôi chọn và nghiên cứu đề tài:
“ ỨNG DỤNG LIÊN HỆ GIỮA DAO ĐỘNG ĐIỀU HÒA VÀ CHUYỂN ĐỘNG
TRÒN ĐỀU ĐỂ GIẢI CÁC BÀI TOÁN TRONG CHƯƠNG DAO ĐỘNG CƠ”
I
II
I.
.
N
Nh
hi
iệ
ệm
m
v
vụ
ụ
v
và
à
p
ph
hư
ươ
ơn
ng
g
p
ph
há
áp
p
n
ng
gh
hi
iê
ên
n
c
cứ
ứu
u
Đề tài này vận dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều để
đưa ra phương pháp giải các dạng bài tập chương dao động cơ.
Trên cơ sở những kết quả đã nghiên cứu chương này sẽ giúp cho các em học sinh
giải quyết được bài tập liên quan ở các chương tiếp theo như Sóng cơ, Điện xoay chiều
hay mạch dao động LC ...
I
II
II
I.
.
P
Ph
hạ
ạm
m
v
vi
i
c
củ
ủa
a
đ
đề
ề
t
tà
ài
i
Đề tài nghiên cứu một vấn đề tương đối khó, đề cập đến các dạng bài tập nâng cao
thường gặp trong đề thi TSĐH, CĐ. Với phạm vi một Sáng kiến - Kinh nghiệm ở
trường THPT chúng tôi chỉ đề cập đến một số vấn đề:
-Phương pháp giải các bài tập phần dao động cơ
-Giới thiệu một số trường hợp vận dụng.
Sáng kiến kinh nghiệm Bùi Thị Thắm-THPT Nguyễn Viết Xuân
3
x
-A A
O P
M
o
M
t
+
B
B.
.N
NỘ
ỘI
I
D
DU
UN
NG
G
I
I.
.C
CƠ
Ơ
S
SỞ
Ở
L
LÍ
Í
T
TH
HU
UY
YẾ
ẾT
T
I
I.
.1
1.
.L
Li
iê
ên
n
h
hệ
ệ
g
gi
iữ
ữa
a
d
da
ao
o
đ
độ
ộn
ng
g
đ
đi
iề
ều
u
h
hò
òa
a
v
và
à
c
ch
hu
uy
yể
ển
n
đ
độ
ộn
ng
g
t
tr
rò
òn
n
đ
đề
ều
u
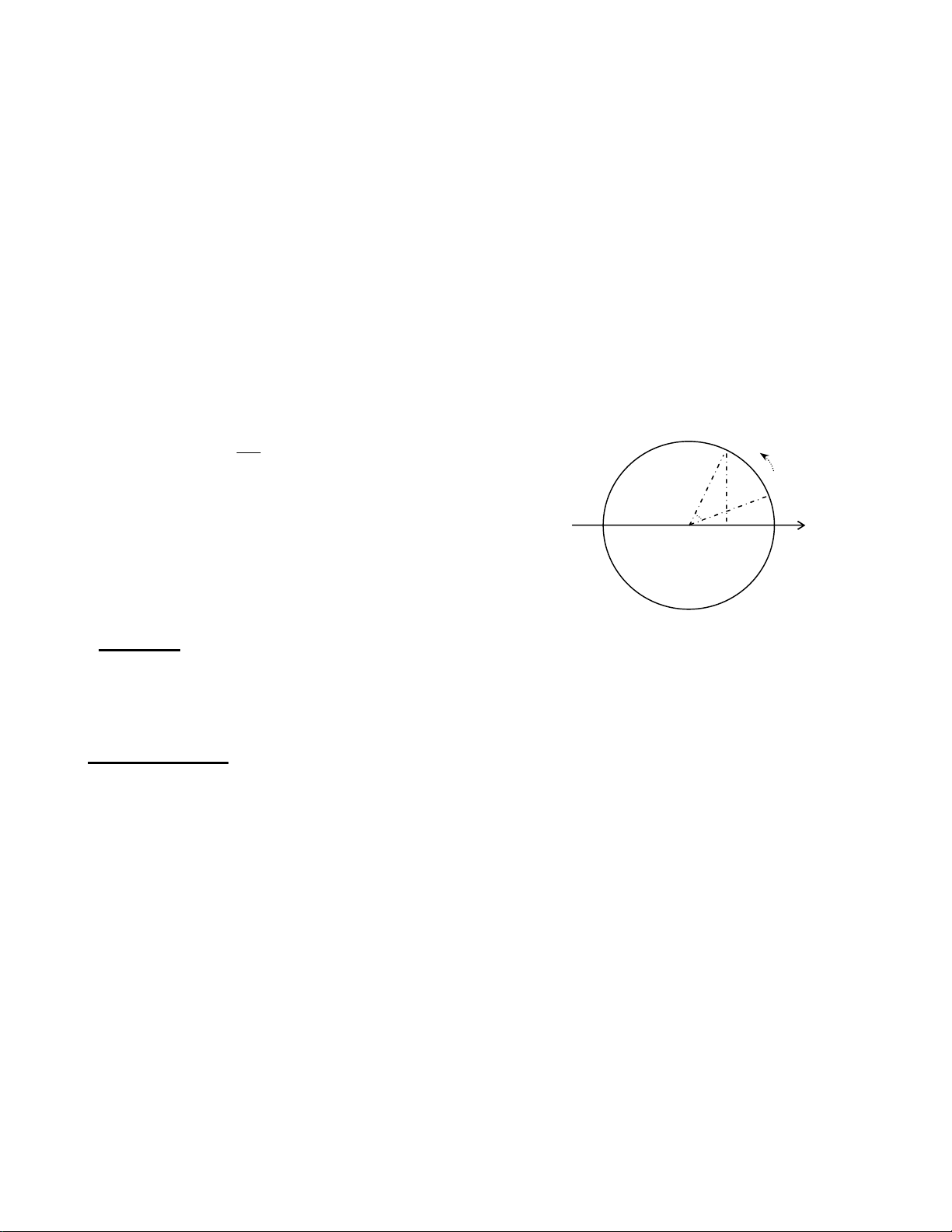
Xét một điểm M chuyển động tròn đều trên đường tròn tâm O theo chiều dương với tốc
độ góc . Gọi P là hình chiếu của M lên trục Ox.
Giả sử ban đầu( t = 0 ) điểm M ở vị trí Mo được xác định bằng góc . Ở thời điểm t, nó
chuyển động đến M, xác định bởi góc: +  với  = t.
Khi đó tọa độ của điểm P là:
x = OP = OM.cos(t + )
Đặt OM = A, phương trình tọa độ của P được viết thành:
x = A.cos(t + ).
Vậy điểm P dao động điều hòa.
*Kết luận: Một dao động điều hòa có thể được coi như hình chiếu của một vật chuyển
động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo.
I.2.Cách xác định vị trí ban đầu của vật.
1.Một số chú ý
+Vật luôn chuyển động theo chiều dương ngược chiều kim đồng hồ vì trong dao
động điều hòa tần số ω dẫn đến góc quay luôn dương.
+Nửa đường tròn trên ứng với chất điểm đi từ A về -A ứng với vùng vật có vận tốc
âm
+Nửa đường tròn dưới ứng với chất điểm đi từ -A về A ứng với vùng vật có vận tốc
dương.
+ Tâm của đường tròn là VTCB 0.
+Bán kính của đường tròn bằng với biên độ dao động: R = A
+Vị trí ban đầu của vật trên đường tròn hợp với chiều dương trục ox một góc .
+ Tốc độ quay của vật trên đường tròn bằng
+ Chiều quay của vật ngược chiều kim đồng hồ.
+ Góc mà bán kính nối vật chuyển động quét được trong quá trình vật chuyển động
tròn đều:  = .t
Sáng kiến kinh nghiệm Bùi Thị Thắm-THPT Nguyễn Viết Xuân
4
2.Cách xác định vị trí ban đầu của vật
Trong các bài toán loại này việc xác định thời điểm ban đầu vật ở đâu là rất quan trọng.
Sau đây tôi xin trình bày một vài trường hợp cơ bản nhất:
Vị trí ban đầu của vật được xét từ thời điểm t=0.Thay vào phương trình li độ và vận tốc
ta có:
os ?
sin ?
x Ac
v
(Để cho nhanh chỉ cần nhớ dấu của v là dấu của –sinφ)
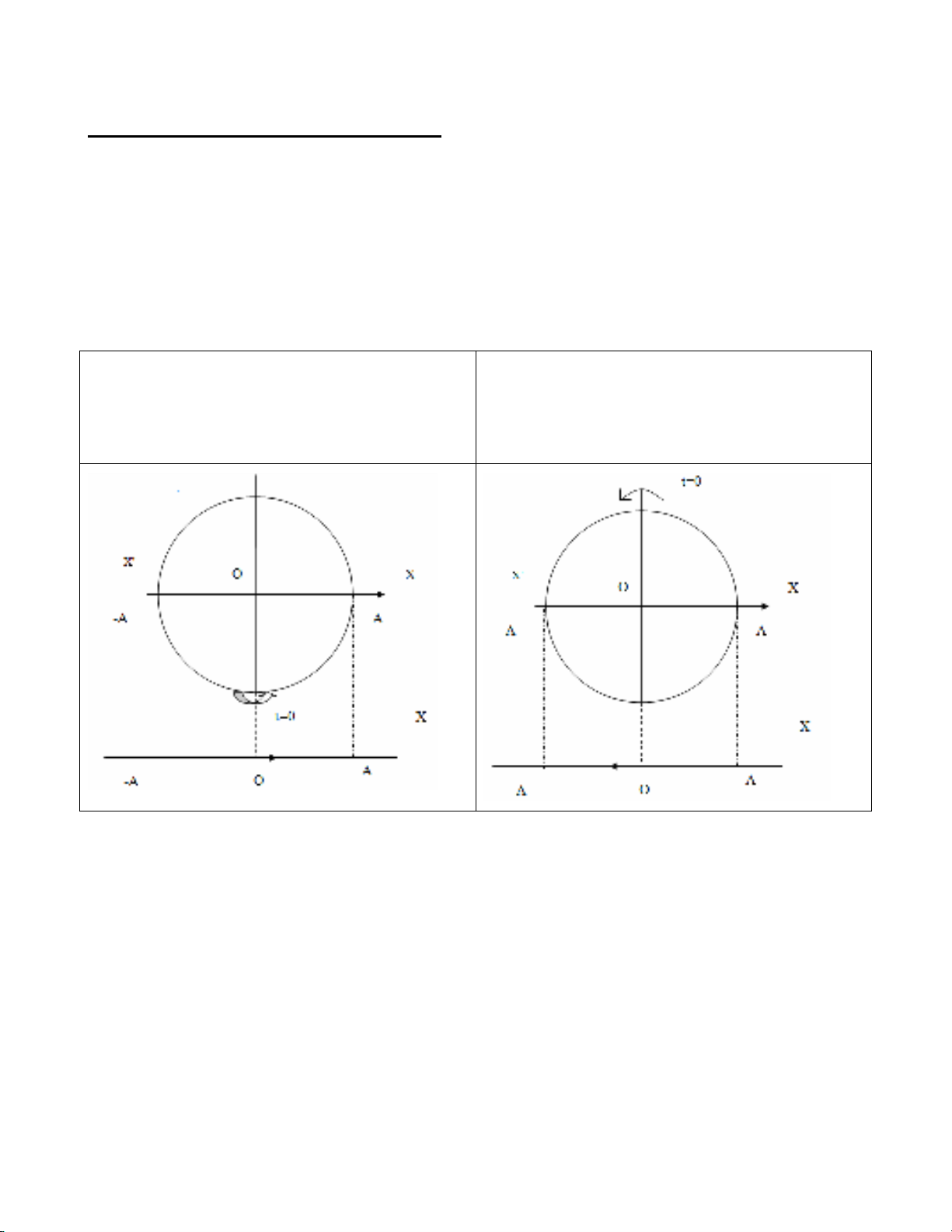
Vật bắt đầu dao động vị trí cân bằng ,vận
tốc dương
Vật bắt đầu dao động vị trí cân bằng ,vận
tốc âm