PHÒNG GD-ĐT ĐẠI LỘC
ĐỀ KIỂMTRA HỌC KỲ II (Năm học 2012-2013)
Môn Toán 9:(thời gian 90 phút)
Họ và tên GV :Hồ Thị Song
Đơn vị :Trường THCS Hoàng Văn Thụ
MA TRẬN ĐỀ KIỂM TRA
Chủ đề hoặc mạch kiến thức,
kĩ năng Trọng
số
Mức độ nhận thức - Hình thức câu hỏi
Tổng điểm
(Theo thang
điểm 10)
Nhận
Biết Thông
Hiểu VD cấp
thấp VD cấp
cao
1. Phương trình bậc hai 4 1 1 1 3
Điểm 1
1,5
1,5
4
2. Giải bài toán bằng cách lập PT 1 1 1
Điểm
1
1
3. Hệ phương trình 1 1 1
Điểm
1
1
4. Góc với đường tròn 4 2 1 3
Điểm
3
1
4
Cộng
Tỷ lệ
% 10 10 80 100
Câu 1 1 7 10
Điểm 1
3
6
10
ĐỀ KIỂM TRA:
Bài 1: (2 đ)
Giải các phương trình và hệ phương trình sau :
a) x2 +5x – 6=0 b)
42
32
yx
yx
Bài 2 :( 3 điểm) Cho phương trình : x2 – 2(m -3)x-1 = 0 (1)
a) Xác định m để phương trình (1) có một nghiệmlà 2.
b) Chứng tỏ rằng phương trình (1) luôn có hai nghiệm trái dấu với mọi m.
Bài 3 (1 đ) Anh hơn em 5 tuổi. Cách đây 5 năm, tuổi anh gấp đôi tuổi em. Hỏi tuổi
của anh và em.
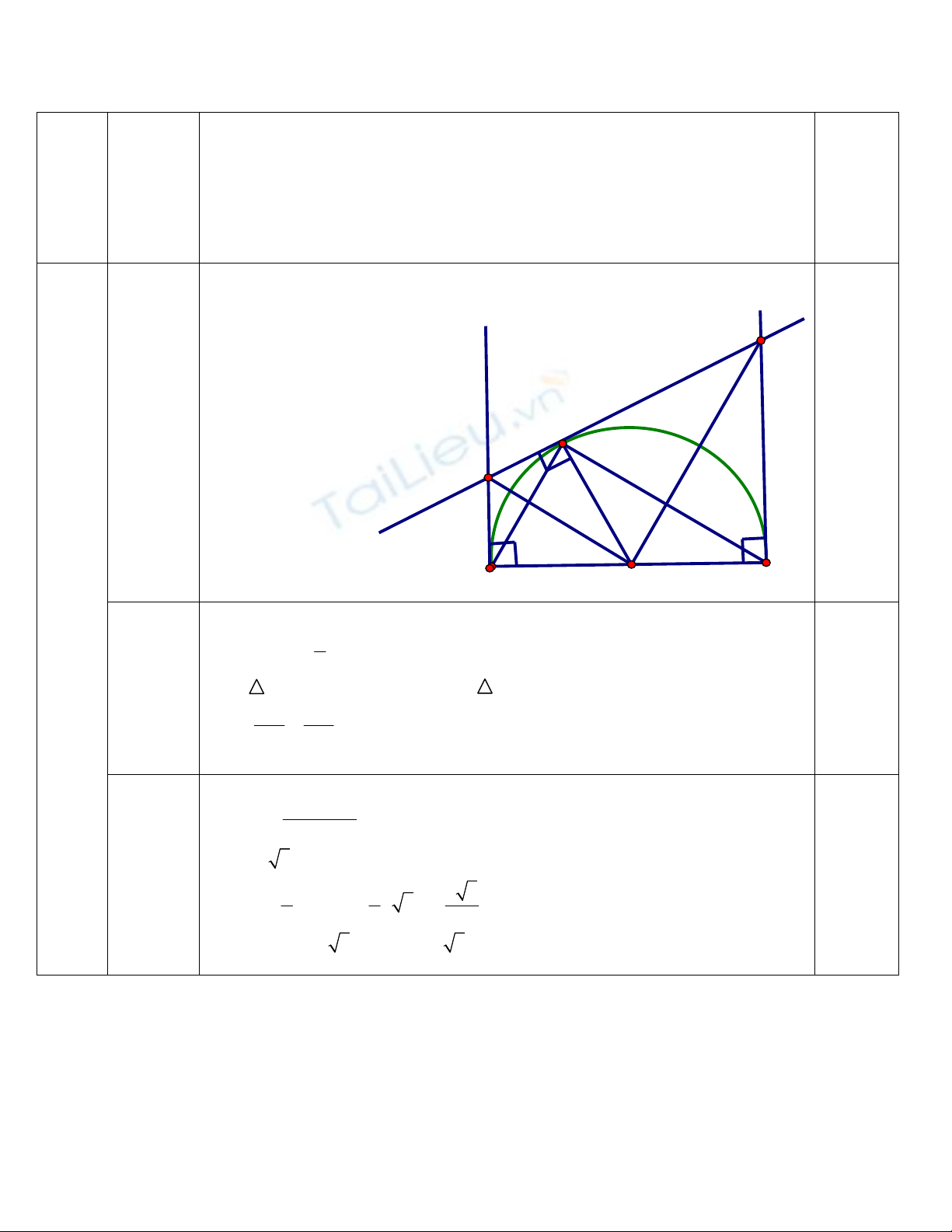
Bài 4: (4 điểm ) Cho nữa đường tròn (O;R) đường kính AB. Qua A, B vẽ các tiếp
tuyến với nữa đường tròn. Từ một điểm M tùy ý trên nữa đường tròn (M ≠ A, B) vẽ
tiếp tuyến thứ ba với nữa đường tròn cắt các tiếp tuyến tại A, B theo thứ tự là H, K.
a) Chứng minh: Tứ giác AHMO nội tiếp
b) Chứng minh: HO.MB = 2R2
c) Cho MOB= 1200 , R = 3cm. Tính diện tích phần mặt phẳng giới hạn bởi hai
tiếp tuyến MK, KB và cung BM .
HƯỚNG DẪN CHẤM TOÁN
BÀI CÂU NỘI DUNG ĐIỂM
1
1a a) x2 +5x-6 = 0 S = {1 ; -6} 1đ
1b b) Hệ pt có nghiệm (2;1) 1đ
2
2a
x2 – 2(m -3)x-1 = 0 (1)
Thay x = 2 được pt : 4(m-3)=3,tìm m = 15/4 1,5
2b a và c trái dấu nên pt luôn có hai nghiệm phân biệt
x1.x2 = -1 <0 nên pt có hai nghiệm trái dấu.
0,75
0,75
3
Gọi tuổi anh và em lần lượt là x,y (x,y
N,x,y > 0)
Lập hệ phương trình :
)5(25
5
yx
yx
Giải hệ phương trình được (x = 15,y =10)
0,25đ
0,5đ
0,25
4
0,25
0,5
5
5a
+ Vẽ hình đúng
Do Ax,By, Mt là
tiếp tuyến của
(O), nên Ax
AB; By AB;
OM Mt =>
0
90
HAO HMO
=> Tứ giác
HAOM nội tiếp
0,5
0,5
0,5
5b
Có góc AOH = góc HOM và Ax , Mt là tiếp tuyến (O)
và
1
( ùng chán cung AM)
2
ABM AOM HOM c
=> vuông HAO đồng dạng vuông AMB
AB MB
=> HO.MB = AO.AB = 2R2
0,5
0,5
0,5
5c
2 0 2
0
.120 3 ( )
360
3 3
1 1 9 3
. 3 3.3
222
q MOB
OBK
R
S cm
KB
S BK OB
S = 9
3 3
= 3(3 3
) cm2
.
0,5
0,25
0,25
t
y
M
K
x
A
H
B
O
Phòng GD-ĐT Đại Lộc ĐỀ THI HỌC KÌ II (Năm học 2012-2013)
Môn : Toán 9 Thời gian : 90 phút
Họ và tên GV ra đề : Nguyễn Thị Huệ
Đơn vị trường THCS Hoàng Văn Thụ
MA TRẬN ĐỀ
Cấp độ
Nội dung
Nhận biết Thông hiểu Vận dụng Cộng
Thấp Cao
Chương 3
Số câu : 2
Tl điểm :
40%
Số câu : 1
Tỉ lệ điểm:
15%
Số câu : 1
Tỉ lệ điểm:
25%
Số câu :2
Tl Số điểm:
40%
Chương 4
Đồ thị của
hs bậc nhất
Số câu : 1
Tl điểm :
20%
Số câu : 1
Tl điểm :
20%
Số câu : 1
Tl điểm : 20%
Chương 3
(Hình)
Số câu : 1
Tl điểm :
40%
Số câu : 1
Tl điểm : 40%
Chương 4
(Hình)
Số câu : 1
Tỉ lệ điểm:
1O%
Số câu : 1
Tỉ lệ điểm:
1O%
Số câu : 1
Tỉ lệ điểm:
1O%
Số câu : 1
Tl điểm : 30%
Cộng
Số câu : 2
Tl điểm :
15%
Số câu : 2
Tỉ lệ điểm:
45%
Số câu : 1
Tl điểm :
40%
Số câu : 1
Tỉ lệ điểm:
1O%
Số câu : 5
Tl điểm :
100%